IBM安置文件|定量分析集– 1

这是IBM定量适度的模型文件。本安置文件将介绍IBM安置中要求的能力，并且严格遵循IBM论文中提出的问题的模式。建议解决以下每个问题，以增加清除IBM展示位置的机会。

1. 找到将除以355、54和103的最大数，以便在每种情况下都保留相同的余数。
   1. 4
   2. 7
   3. 9
   4. 13

   回答：

   7
   

   解释：

   Required number = H.C.F. of |a -b|, |b – c| and |c – a|
   = H.C.F. of |355 – 54|, |54 – 103| and |103 – 355|
   = 301, 49, 252
   = 7

2. 六个钟声开始鸣响，分别以3、6、9、12、15和18秒的间隔鸣响。在60分钟内，他们会共同收费多少次?
   1. 10
   2. 20
   3. 21岁
   4. 25

   回答：

   21
   

   解释：

   L.C.M. of 3, 6, 9, 12, 15 and 18 is 180.
   So, the bells will toll together after every 180 seconds(3 minutes).
   In 60 minutes, they will toll together (60/3)+1 = 21 times.

3. 可以被11整除的最小5位数字是：
   1. 11121
   2. 11011
   3. 10010
   4. 11000

   回答：

   10010
   

   解释：

   The smallest 5-digit number 10000.

   10000 when divided by 11, leaves a remainder of 1

   Hence add (11 – 1) = 10 to 10000
   Therefore, 10010 is the smallest 5 digit number exactly divisible by 11

4. 
   1. 474
   2. 534
   3. 500
   4. 368

   回答：

   474
   

   解释：

   As
   

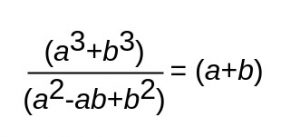
   Therefore the given expression = (121 + 353) = 474

5. 一分钟等于十小时的小数?
   1. 0.025
   2. 0.256
   3. 0.0027
   4. 0.00126

   回答：

   0.0027
   

   解释：

   Decimal of 10 hours in a minute
   = 10 / (60 x 60)
   = 0.0027

6. “ A”可以在10天内完成工作，“ B”可以在15天内完成工作。如果他们一起工作3天，那么剩下的工作是：
   1. 10％
   2. 20％
   3. 40％
   4. 50％

   回答：

   50%
   

   解释：

   Let the total work to be done is, say, 30 units.

   A does the work in 10 days,
   So A’s 1-day work = (30 / 10) = 3 units

   B does the work in 15 days,
   So B’s 1-day work = (30 / 15) = 2 units

   Therefore, A’s and B’s together 1-day work = (3 + 2) = 5 units

   In 3 days,
   work done = 5 * 3 = 15 units
   amount of work left = 30 – 15 = 15 units

   Therefore the % of work left after 3 days = (15 / 30) * 100% = 50%

7. 泵可以在1小时内向水箱注满水。由于泄漏，需要花费1.5个小时来填充油箱。泄漏会排掉以下箱中的所有水：
   1. 2小时
   2. 2.5小时
   3. 3小时
   4. 3.5小时

   回答：

   3 hours
   

   解释：

   Pump fills the tank in 1 hour

   Time taken by Pump to fill due to leak = 1.5 hour
   Therefore, in 1 hour, the amount of tank that the Pump can fill at this rate = 1 / (1.5) = 2/3

   Amount of water drained by the leak in 1 hour = (1 – (2/3)) = 1/3

   Therefore, the tank will be completely drained by the leak in (1 / (1/3)) = 3 hours

8. 2条管道A和B可以分别在20分钟和30分钟内填充一个水箱。两个管道都打开。如果B在以下情况下关闭，则仅需15分钟即可填充水箱：
   1. 5分钟
   2. 6.5分钟
   3. 7分钟
   4. 7.5分钟

   回答：

   7.5 min
   

   解释：

   Let the total work to be done is, say, 60 units.

   A fills the tank in 20 minutes,
   So A’s 1-minute work = (60 / 20) = 3 units

   B fills the tank in 30 minutes,
   So B’s 1-minute work = (60 / 30) = 2 units

   Therefore, A’s and B’s together 1-minute work = (3 + 2) = 5 units

   Let the time when A and B both are opened be x minutes
   and Since the total time taken to fill the tank is 15 minutes

   Therefore, an expression can be formed as
   5x + 3(15 – x) = 15
   => x = 7.5

   Therefore, the B is turned off after 7.5 minutes

9. 在IPL比赛中，CSK当前的运行速度是4.5 in 6 overs。为了实现KKR达到153的目标，CSK的要求运行率应该是多少?
   1. 7
   2. 8
   3. 8.5
   4. 9

   回答：

   9
   

   解释：

   Current run rate = 4.5 in 6 overs
   Runs already made = 4.5 * 6 = 27

   Target = 153
   Runs still required = 153 – 27 = 126
   Overs left = 14

   Therefore required run rate = 126 / 14 = 9

10. 10个数字的平均值为0。其中，最多有多少个数字可以比零大?
    1. 0
    2. 1个
    3. 9
    4. 10

    回答：

    9
    

    解释：

    Let the 9 numbers be smaller than zero and let their sum be ‘s’

    Now, in order to get the average 0, the 10th number can be ‘-s’

    Therefore, average = (s + (-s))/10 = 0/10 = 0

11. 哪个不是素数? 。
    1. 43
    2. 57
    3. 73
    4. 101

    回答：

    57
    

    解释：

    A positive natural number is called prime number if nothing divides it except the number itself and 1.
    57 is not a prime number as it is divisible by 3 and 19 also, apart from 1 and 57.

12. 如果四个连续奇数的平均值是12，那么找到这些数字中最小的那个了吗?
    1. 5
    2. 7
    3. 9
    4. 11

    回答：

    9
    

    解释：

    Let the numbers be x, x+2, x+4 and x+6
    Then (x + x + 2 + x + 4 + x + 6)/4 = 12
    ∴ 4x + 12 = 48
    ∴ x = 9

13. 两个数字的比例为2：9。如果他们的HCF为19，则数字为：
    1. 6、27
    2. 8、36
    3. 38、171
    4. 20、90

    回答：

    38, 171
    

    解释：

    Let the numbers be 2X and 9X
    Then their H.C.F. is X, so X = 19
    ∴ Numbers are (2×19 and 9×19) i.e. 38 and 171

14. 两个数字的HCF为11，而LCM为385。如果两个数字的相差不超过50，那么两个数字的总和是多少?
    1. 132
    2. 35
    3. 12
    4. 36

    回答：

    132
    

    解释：

    Product of numbers = LCM x HCF
    => 4235 = 11 x 385

    Let the numbers be of the form 11m and 11n,
    such that ‘m’ and ‘n’ are co-primes.
    => 11m x 11n = 4235
    => m x n = 35
    => (m, n) can be either of (1, 35), (35, 1), (5, 7), (7, 5).
    => The numbers can be (11, 385), (385, 11), (55, 77), (77, 55).

    But it is given that the numbers cannot differ by more than 50.
    Hence, the numbers are 55 and 77.
    Therefore, sum of the two numbers = 55 + 77 = 132

15. 一个人雇用了一组20人从事建筑工作。这20个人每天工作8小时，可以在28天内完成工作。这项工作按时开始，但在18天后，发现仍有三分之二的工作仍在进行中。为了避免罚款并按时完成工作，雇主必须雇用更多的工人，并且还将工作时间增加到每天9个小时。如果所有男性的效率相同，则找到更多的男性雇佣人数。
    1. 40
    2. 44
    3. 64
    4. 80

    回答：

    44
    

    解释：

    Let the total work be 3 units and additional men employed after 18 days be ‘x’.
    => Work done in first 18 days by 20 men working 8 hours a day = (1/3) x 3 = 1 unit
    => Work done in last 10 days by (20 + x) men working 9 hours a day = (2/3) x 3 = 2 unit

    Here, we need to apply the formula

    where
    M1 = 20 men
    D1 = 18 days
    H1 = 8 hours/day
    W1 = 1 unit
    E1 = E2 = Efficiency of each man
    M2 = (20 + x) men
    D2 = 10 days
    H2 = 9 hours/day
    W2 = 2 unit

    So, we have
    20 x 18 x 8 / 1 = (20 + x) x 10 x 9 / 2
    => x + 20 = 64
    => x = 44

    Therefore, number of additional men employed = 44

16. 两个出口管A和B连接到一个已满的水箱。单独的管道A可以在10分钟内清空储罐，而单独的管道B可以在30分钟内清空储罐。如果将两者一起打开，则要花多少时间才能完全清空水箱?
    1. 7分钟
    2. 7分30秒
    3. 6分钟
    4. 6分30秒

    回答：

    M1 D1 H1 E1 / W1 = M2 D2 H2 E2 / W2,
    

    解释：

    Let the capacity of the tank be LCM(10, 30) = 30 units.
    => Efficiency of pipe A = 30 / 10 = 3 units / minute
    => Efficiency of pipe A = 30 / 30 = 1 units / minute
    => Combined efficiency of pipe A and pipe B = 4 units / minute

    Therefore, time required to empty the tank
    if both pipes work = 30 / 4 = 7 minutes 30 seconds

17. 三个管道A，B和C连接到水箱。单独工作，它们分别需要10个小时，20个小时和30个小时。一段时间后，A关闭，再过2个小时，B也关闭。 C会再工作14个小时，以使水箱完全充满。找到关闭管道A的时间(以小时为单位)。
    1. 1个
    2. 1.5
    3. 2个
    4. 3

    回答：

    7 minutes 30 seconds
    

    解释：

    Let the capacity of the tank be LCM (10, 20, 30) = 60
    => Efficiency of pipe A = 60 / 10 = 6 units / hour
    => Efficiency of pipe B = 60 / 20 = 3 units / hour
    => Efficiency of pipe C = 60 / 30 = 2 units / hour

    Now, all three work for some time, say ‘t’ hours.
    So, B and C work for 2 more hours after ‘t’ hours
    and then, C works for another 14 hours.

    => Combined efficiency of pipe A, pipe B and pipe C = 11 units / hour
    => Combined efficiency of pipe B and pipe C = 5 units / hour

    So, we have 11 x t + 5 x 2 + 14 x 2 = 60
    => 11 t + 10 + 28 = 60
    => 11 t = 60 – 38
    => 11 t = 22
    => t = 2

    Therefore, A was closed after 2 hours.

18. 两辆速度分别为15 kmph和30 kmph的汽车相距100 km，并且彼此面对。穿越前5分钟，他们之间的距离是
    1. 2.75
    2. 3.75
    3. 4.75
    4. 5.75

    回答：

    2
    

    解释：

    As the two cars are moving towards each other,
    their relative speed will be = 15+30 = 45 kmph.

    The distance between them 5 minutes before crossing
    will be equal to the distance travelled by their relative speed in 5 minutes,
    i.e. Required distance = Relative speed (in km per min) * time (in minutes) = (45/60)*5 = 3.75 km.