泰雷斯定理

定理陈述：Thales定理或基本比例定理指出，如果平行于三角形的一侧画一条线，且该三角形的另一侧在不同的点相交，则其他两侧将以相同的比率划分。

基本比例定理的证明

Suppose we have a triangle ABC, if we draw a line LM parallel to side BC then the theorem states that,

$\frac{AP}{PB}=\frac{AQ}{QC}$ 

In triangle ABC, join the vertex B to M on line AC and join vertex C on line AB. Then, drop a perpendicular MX on line AB and perpendicular LY on AC. The below diagram shows the construction for the same.

Since, area of triangle= $(\frac{1}{2}*base*height)$

Area of $\triangle$ALM=$(\frac{1}{2}*AL*MX)$

Area of $\triangle$LBM=$(\frac{1}{2}*LB*MX)$

Area of $\triangle$ALM=$(\frac{1}{2}*AM*LY)$

Area of $\triangle$LMC=$(\frac{1}{2}*MC*LY)$

Ratio of area of $\triangle$ALM and $\triangle$LBM:

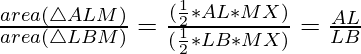$\frac{area(\triangle ALM)}{area(\triangle LBM)}=\frac{(\frac{1}{2}*AL*MX)}{(\frac{1}{2}*LB*MX)}=\frac{AL}{LB}$—-(1)

Ratio of area of $\triangle$ALM and $\triangle$LMC:

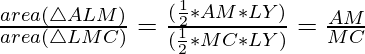$\frac{area(\triangle ALM)}{area(\triangle LMC)}=\frac{(\frac{1}{2}*AM*LY)}{(\frac{1}{2}*MC*LY)}=\frac{AM}{MC}$—-(2)

According to the property of triangles, the triangles on the same base and between same parallel lines have equal areas.

Therefore, $\triangle$LBM and $\triangle$LMC have equal areas.—-(3)

From equations (1),(2), and (3) we can conclude:

$\frac{AL}{LB}=\frac{AM}{MC}$

因此，证明了基本的比例定理。

基本比例定理的求解示例

示例1.在∆ABC中，AB面和AC面分别在D和E处与直线BC相交。证明AD / AB = AE / AC。

解决方案：

Given: DE || BC. So, AD/DB = AE/EC

or By interchanging the ratios as => DB/AD = EC/AE

Now, add 1 on both sides=> (DB/AD)  + 1 = (EC/AE) + 1

                                               (DB + AD)/AD = (EC + AE)/AE

                                               AB/AD = AC/ AE

If we interchange the ratios again, we get=> AD/AB = AE/AC

Hence, proved.

示例2.在三角形ABC中，其中DE是从AB中点画出的线，并在E处结束AC的中点。AD / DB = AE / EC和∠ADE=∠ACB。然后证明ABC是等腰三角形。

解决方案：

Given: AD/DB = AE/EC

By the converse of the basic proportionality theorem, we get => DE || BC

According to question => ∠ADE = ∠ACB

Hence,∠ABC = ∠ACB

The side opposite to equal angles is also equal to AB = AC

Hence, ABC is an isosceles triangle.