具有相同形状但大小不同的几何图形被称为相似图形。两个一致的数字总是相似的,但是两个相似的数字不必是一致的。
例子
(i) Any two line segments are similar.
(ii) Any two equivalent triangles are similar.
(iii) Any two rectangles are similar.
(iv) Any two squares are similar.
(v) Any two circles are similar.
相似三角形
如果两个三角形被称为彼此相似,
- 它们对应的角度相等,并且
- 它们对应的边成比例。
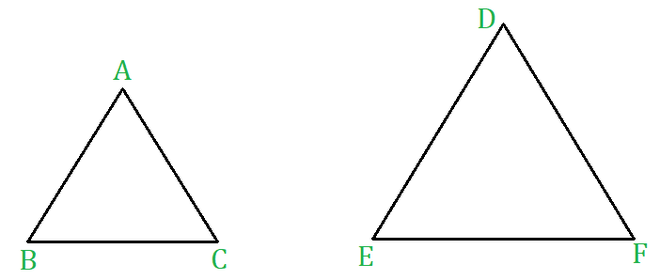
相似三角形
In △ABC and △DEF if (i) ∠A = ∠D , ∠B = ∠E, ∠C = ∠F
and (ii) AB/DE = BC/EF = CA/FD
Then above two triangles are similar, i.e. △ABC ∼ △DEF.
相似三角形的结果
基本比例定理或Thales定理
Theorem: If a line is drawn parallel to one side of a triangle to intersect the other two sides in distinct points then the other two sides are divided in the same ratio.

证明:
Given: A △ABC in which DE || BC and DE intersects AB and AC at D and E respectively.
To Prove: AD/DB = AE/EC
Construction: Join BE and CD. Draw EL ⟂ AB and DM ⟂ AC.
We have: area (△ADE) =1/2 (AD x EL)
area (△DBE) = 1/2(DB x EL)
∴ area(△ADE)/area(△DBE) =(1/2x AD x EL)/(1/2x DB x EL) = AD/DB …………(i)
Again, area(△ADE) = area(△AED) = (1/2x AE x DM)
area(△ECD) = (1/2x EC x DM)
∴ area(△ADE)/area(△ECD) = (1/2 x AE x DM)/(1/2 x EC x DM) = AE/EC ……….(ii)
Now △DBE and △ECD being on the same base DE and between the same parallels DE and BC , we have:
area(△DBE)/area(△ECD) ……….(iii)
From eqn(i) and eqn(ii)
AD/DB = AE/EC
泰勒斯定理的例子
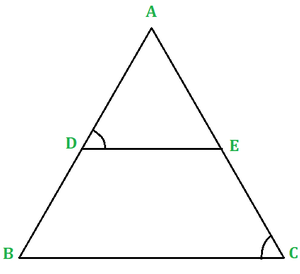
图1
示例1:在给定的图1中,DE ||公元前。如果AD = 2.5厘米,DB = 3厘米和AE = 3.75厘米,找到AC吗?
解决方案:
In △ABC, DE || BC
AD/DB = AE/EC (By Thales’ Theorem)
⇒ 2.5/3 = 3.75/x, where EC = x cm
⇒ (3 * 3.75)/2.5 = 9/2 = 4.5
⇒ EC = 4.5cm
Hence, AC = (AE + EC) = 3.75 + 4.5 = 8.25 cm.
示例2:在图中1 DE || BC.AD = 1.7厘米,AB = 6.8厘米,AC = 9厘米,找到AE?
解决方案:
Let AE = x cm.
In △ABC, DE || BC
By Thales Theorem we have,
AD/AB = AE/AC
⇒ 1.7/6.8 = x/9
⇒ x = (1.7*9)/6.8 = 2.25
⇒ AE = 2.25cm
Hence AE = 2.25cm
例3:证明一条通过三角形的另一边(图1)平行于另一边的中点画出的线将第三边平分。
解决方案:
Given a ΔΑΒC in which D is the midpoint of AB and DE || BC, meeting AC at E.
TO PROVE AE = EC.
Proof: Since DE || BC, by Thales’ theorem, we have:
AE/AD = EC/DB =1 (AD = DB, given)
AE/EC = 1
⇒ AE = EC.
泰勒斯定理的反面
Theorem: (Converse of Thales’ theorem) If a line divides any two sides of triangle in the same ratio then the line must be parallel to the third side.
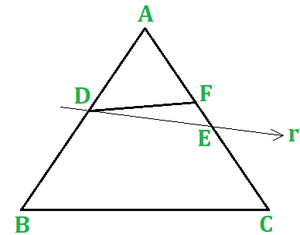
证明:
Given: A △ABC and a line r intersecting AB at D and AC at E, such that AD/DB = AE/EC
To prove: DE || BC
Proof: If possible, let DE not be parallel to BC. Then, there must be another line through D, which is parallel to BC.
Let DF || BC
Then by Thales Theorem,
AD/DB = AF/FC ……….(i)
But, AD/DB = AE/EC (given) ……..(ii)
From eqn(i) and eqn(ii)
AF/FC = AE/EC ⇒ AF/FC + 1 = AE/EC + 1
(AF + FC)/FC = (AE + EC)/EC
AC/FC = AC/EC ⇒ 1/FC = 1/EC
⇒ FC = EC.
This is possible only when E and F coincide.
Hence, DE || BC.
基于泰勒斯定理的逆的例子

图2
示例1:在给定的图2中,AD / DB = AE / EC,而ADE = ACB。证明ABC是等腰三角形。
解决方案:
We have AD/DB = AE/EC ⇒ DE || BC [by the converse of Thales’ theorem]
∠ADE = ∠ABC (corresponding ∠s)
But, ∠ADE = ∠ACB (given).
Hence, ∠ABC = ∠ACB.
So, AB = AC [sides opposite to equal angles].
Hence, △ABC is an isosceles triangle.
例2:如果D和E分别是△ABC的AB和AC侧的点(图2),使得AB = 5.6cm,AD = 1.4cm,AC = 7.2cm,AE = 1.8cm,则DE | DE |公元前。
解决方案:
Given, AB = 5.6cm, AD = 1.4cm, AC = 7.2cm and AE = 1.8cm
AD/AB = 1.4/5.6 = 1/4 and AE/AC = 1.8/7.2 = 1/4
⇒ AD/AB = AE/AC
Hence, by converse of Thales Theorem, DE || BC.
示例3:证明连接三角形任意两个边的中点的线段(图2)与第三边平行。
解决方案:
In △ABC in which D and E are the midpoints of AB and AC respectively.
Since D and E are the midpoints of AB and AC respectively, we have :
AD = DB and AE = EC.
AD/DB = AE/EC (each equal to 1)
Hence, by converse of Thales Theorem, DE || BC