相似三角形的构造

基本的构造技术允许构造垂直平分线，角度平分线等。这些基本技术可用于更复杂的结构。这些结构对于设计建筑物，道路，机器等的设计师来说非常重要。因此，这些技术在现实生活中非常方便。顾名思义，相似的三角形是指外观，角度和边长比相似的三角形。但是，如果给出了一个三角形并被要求制作一个类似的三角形，该如何做呢?是否需要再次构造整个三角形?为此，开发了一些构造技术以简化该过程。

相似三角形

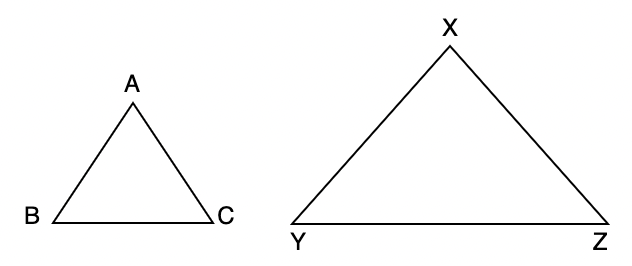
相似的三角形是不相等的三角形，但它们在本质上相似。当两个三角形相似时，必须满足一些条件。

Let’s say we have two triangles which are similar ΔABC and ΔXYZ. The two triangles must follow two conditions: 

1. The corresponding angles of the triangles must be equal 

∠A = ∠X, ∠B = ∠ Y and ∠ C = ∠ Z

2. The corresponding sides of both the triangles must be in same ratio. 

$\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX}$

相似三角形的构造

相似三角形的这种构造涉及两种情况：

1. 要构造的三角形大于原始三角形
2. 要构造的三角形小于原始三角形。

Scale Ratio: We define scale ratio as the ratio of the sides of the triangle constructed with the sides of the original triangle. 

样品结构

让我们通过一些示例来了解这两种情况的构造，

问题1：以比例比=构造类似于三角形ΔPQR的三角形$\frac{3}{4}$

解决方案：

We know that the scale ratio must be $\frac{3}{4}$, that is the sides of the new triangle must be $\frac{3}{4}th$, of the sides of the original triangle. 

Steps of Construction: 

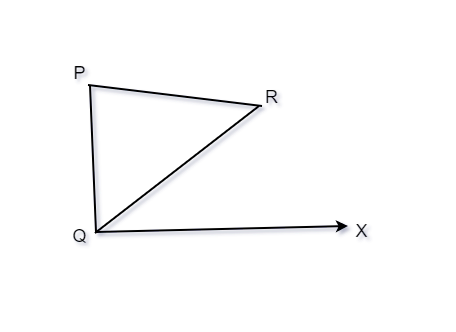
Step 1. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P. 

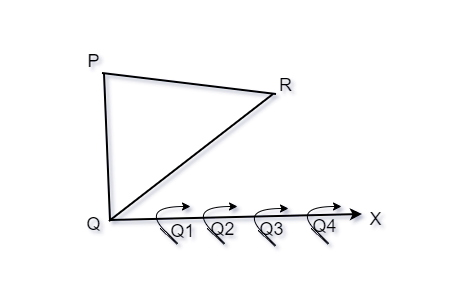
Step 2. On the ray QX, make four points Q₁, Q₂, Q₃ and Q₄ on QX in such a way that QQ₁ = QQ₂ = QQ₃ = QQ₄. Now on this ray locate the 4th point(whichever is greater in the fraction $\frac{3}{4}$

Step 3. Now join Q₄R and draw a line from Q₃ parallel to Q₄R and let it intersect QR at R’.

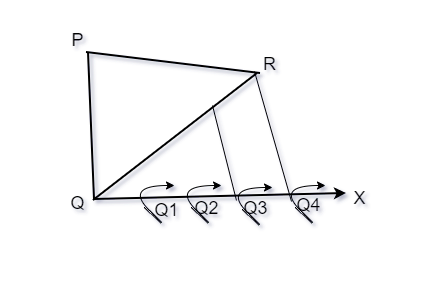
Step 4. Draw a line from R’ which is parallel to the line RP. Let it intersect PQ and P’ 

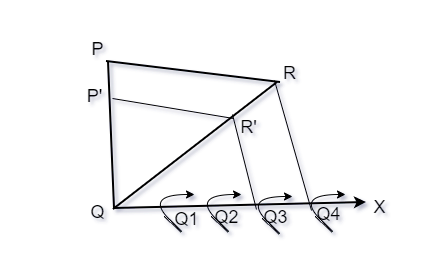
ΔPQ’R’ is our required triangle. 

问题2：以比例比=构造类似于三角形ΔPQR的三角形$\frac{5}{3}$ 。

解决方案：

This is an example of the second case, scale ratio is given by $\frac{5}{3}$. That is the sides of the new triangle must be $\frac{5}{3}rd$, of the sides of the original triangle. The steps in this case are similar to the above case, but with some minor modification. 

Steps for Construction:

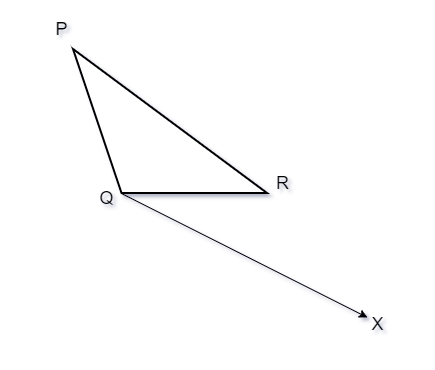
Step 1. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P. 

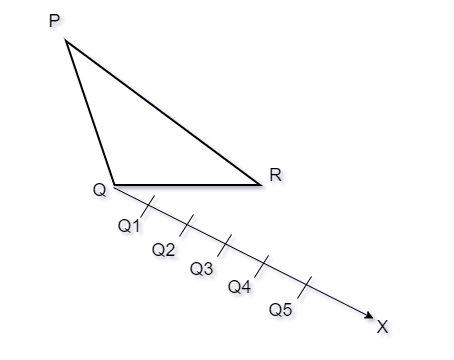
Step 2. On the ray QX, make four points Q₁, Q₂, Q_3, Q_4, Q₅on QX in such a way that QQ₁ = QQ₂ = QQ₃ = QQ₄ = QQ₅. Now on this ray locate the 5th point whichever is greater in the fraction $\frac{5}{3}$ 

Step 3. Join the 3rd point with R and draw a line that is parallel to Q₃R through the 5th point, let it intersect the extended line QR at R’.

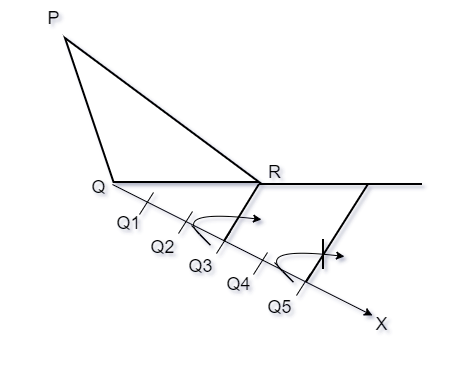
Step 4. Now, we need to draw the line through R’ which parallel to PR, it should intersect the extended line of PQ and P’. 

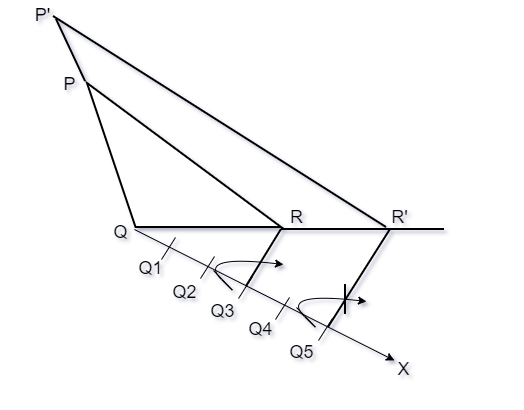
ΔP’QR’ is our required triangle. 

问题3：画一个边长为10cm，11cm和8cm的三角形。然后绘制一个与其比例相似的三角形$\frac{2}{3}$ 。

解决方案：

Steps of the construction: 

Step 1. Draw a triangle of 10cm, 11cm and 8cm. 

We know that the scale ratio must be $\frac{2}{3}rd$, that is the sides of the new triangle must be $\frac{2}{3}rd$, of the sides of the original triangle. 

Step 2. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P. 

Step 2. On the ray QX, make three points Q₁, Q₂, Q₃ on QX in such a way that QQ₁ = QQ₂ = QQ₃. Now on this ray locate the 2nd point(whichever is greater in the fraction $\frac{2}{3}$

Step 3. Now join Q₃R and draw a line from Q₂ parallel to Q₃R and let it intersect QR at R’.

Step 4. Draw a line from R’ which is parallel to the line RP. Let it intersect PQ and P’ 

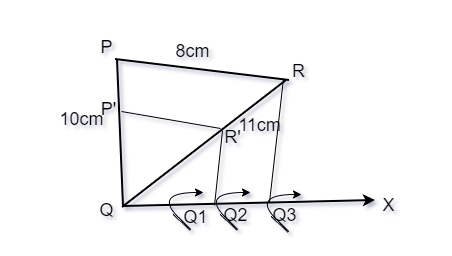
ΔPQ’R’ is our required triangle. 

问题4：在上一个问题的原始三角形中。绘制一个与其比例类似的三角形$\frac{4}{3}$ 。

解决方案：

Steps of the construction: 

Step 1. Draw a triangle of 10cm, 11cm and 8cm. 

We know that the scale ratio must be $\frac{4}{3}rd$, that is the sides of the new triangle must be $\frac{4}{3}rd$, of the sides of the original triangle. 

Step 2. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P. 

Step 3. On the ray QX, make four points Q₁, Q₂, Q_3, Q_4, Q₅on QX in such a way that QQ₁ = QQ₂ = QQ₃ = QQ₄ = QQ₅. Now on this ray locate the 5th point whichever is greater in the fraction $\frac{5}{3}$ 

Step 4. Join the 3rd point with R and draw a line that is parallel to Q₃R through the 5th point, let it intersect the extended line QR at R’.

Step 5. Now, we need to draw the line through R’ which parallel to PR, it should intersect the extended line of PQ and P’. 

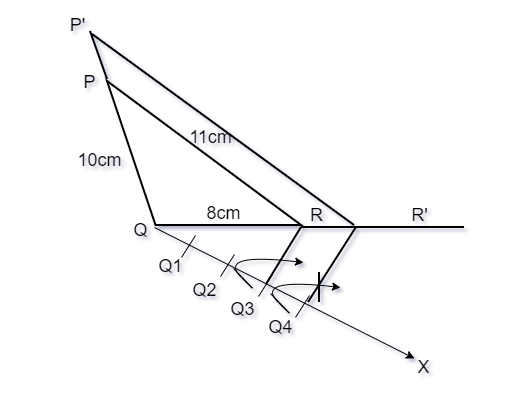
ΔP’QR’ is our required triangle. 

问题5：画一个边长4cm，5cm和6cm的三角形。然后绘制一个与其比例相似的三角形$\frac{2}{3}$ 。

解决方案：

Steps of the construction: 

Step 1. Draw a triangle of 4cm, 5cm and 6cm. 

We know that the scale ratio must be $\frac{2}{3}rd$, that is the sides of the new triangle must be $\frac{2}{3}rd$, of the sides of the original triangle. 

Step 2. Draw a ray QX which makes acute angle with QR on the side that is opposite to the P. 

Step 2. On the ray QX, make three points Q₁, Q₂, Q₃ on QX in such a way that QQ₁ = QQ₂ = QQ₃. Now on this ray locate the 2nd point(whichever is greater in the fraction $\frac{2}{3}$

Step 3. Now join Q₃R and draw a line from Q₂ parallel to Q₃R and let it intersect QR at R’.

Step 4. Draw a line from R’ which is parallel to the line RP. Let it intersect PQ and P’. 

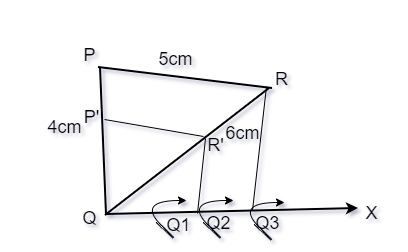
ΔPQ’R’ is our required triangle.