平行四边形的属性

两对相对的边相等的四边形是平行四边形。平行四边形是二维几何形状，其边彼此平行。以下是有关平行四边形的一些简单事实：

1. 平行四边形的边数= 4
2. 平行四边形中的顶点数= 4
3. 面积=基础x高度
4. 周长= 2(相邻边的长度之和)
5. 多边形类型=四边形

以下是平行四边形的表示：

证明：平行四边形

证明1：平行四边形的对边相等。

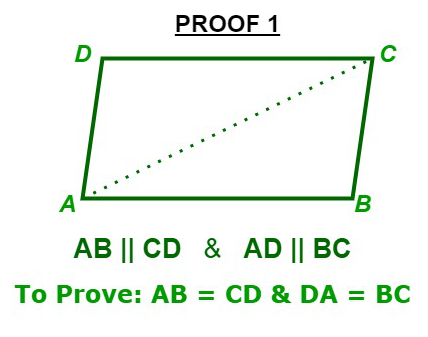
Given: ABCD is a parallelogram
 

To Prove: AB = CD & DA = BC

Firstly, Join AC

As given ABCD is a parallelogram. Therefore, 

AB || DC  &  AD || BC

Now,  AD || BC and AC is intersecting A and C respectively.

$\angle$DAC = $\angle$BCA                   …(i)                  [Alternate Interior Angles]

Now, AB || DC and AC is intersecting A and C respectively.

$\angle$BAC = $\angle$DCA                 …(ii)                      [Alternate Interior Angles]

Now, In $\triangle$ADC & $\triangle$CBA

$\angle$DAC = $\angle$BCA                    [ From (i) ]

AC = AC                                   [ Common Side ]

$\angle$DCA = $\angle$BAC                 [ From (ii) ]

So, by ASA(Angle-Side-Angle) criterion of congurence

$\triangle$ADC  $\cong$ $\triangle$CBA

AB = CD & DA = BC [ Corresponding part of congurent triangles are equal ]

Hence Proved !

证明2：平行四边形的对角相等。

Given: ABCD is a parallelogram

To Prove:  $\angle$A = $\angle$C  and $\angle$B = $\angle$D

As given ABCD is a parallelogram. Therefore, 

AB || DC  &  AD || BC

Now, AB || DC and AD is Intersecting them at A and D respectively.

$\angle$A + $\angle$D = 180$\degree$               …(i)             [ Sum of consecutive interior angles is 180$\degree$]

Now, AD || BC and DC is Intersecting them at D and C respectively.

$\angle$D + $\angle$C = 180$\degree$              …(ii)            [ Sum of consecutive interior angles is 180\degree]

From (i) and (ii) , we get

$\angle$A + $\angle$D = $\angle$D  +  $\angle$C

So,  $\angle$A = $\angle$C

Similarly, $\angle$B = $\angle$D

$\angle$A = $\angle$C and  $\angle$B = $\angle$D

Hence Proved !

证明3：平行四边形的对角线一分为二。

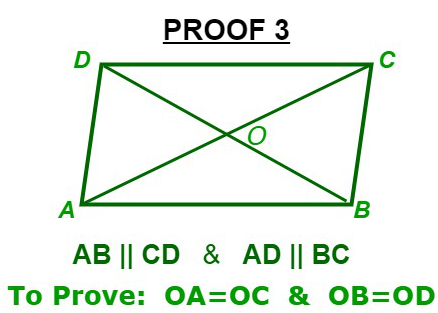
Given: ABCD is a parallelogram

To Prove: OA = OC & OB = OD

As given ABCD is a parallelogram. Therefore,

AB || DC  &  AD || BC

Now, AB || DC and AC is intersecting A and C respectively.

$\angle$BAC = $\angle$DCA                               [ Alternate Interior Angles are equal ]

So, $\angle$BAO = $\angle$DCO

Now,  AB || DC and BD is intersecting B and D respectively.

$\angle$ABD = $\angle$CDB                               [ Alternate Interior Angles are equal ]

So, $\angle$ABO = $\angle$CDO

Now, in  $\triangle$AOB &  $\triangle$COD we have, 

$\angle$BAO = $\angle$DCO                               [ Opposite sides of a parallelogram are equal ]

AB = CD

$\angle$ABO = $\angle$CDO

So, by ASA(Angle-Side-Angle) congurence criterion 

$\triangle$AOB  $\cong$  $\triangle$COD

OA = OC and OB = OD

Hence Proved !