9类NCERT解决方案-第13章表面积和体积–练习13.8

问题1：找出半径为的球体的体积

(i)7厘米(ii)0.63 m(假设π= 22/7)

解决方案：

(i) Given: Radius of sphere, r = 7 cm

By using the formula, volume of sphere = (4/3) πr³

= (4/3)×(22/7)×(7)³

= 4312/3 cm³

Therefore, the volume of the sphere is 4312/3 cm³

(ii) Given: Radius of sphere, r = 0.63 m

By using the formula, volume of sphere = (4/3) πr³

= (4/3)×(22/7)×(0.63)³

= 1.0478 m³

Therefore, the volume of the sphere is 1.05 m³ (approx).

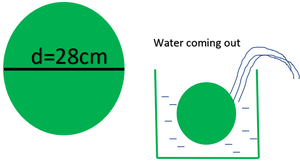
问题2：求出直径为实心的球形球所排出的水量

(i)28厘米(ii)0.21 m(假设π= 22/7)

解决方案：

(i) Given: Diameter = 28 cm

Therefore, the radius, r = 28/2 cm = 14cm

By using the formula, volume of the solid spherical ball = (4/3) πr³

= (4/3)×(22/7)×(14)³

= 34496/3 cm³

Therefore, the volume of the ball is 34496/3 cm³

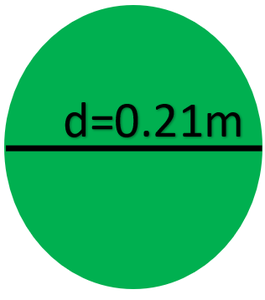
(ii) Given: Diameter = 0.21 m

Therefore, the radius of the ball =0.21/2 m= 0.105 m

By using the formula, volume of the ball = (4/3 )πr³

= (4/3)× (22/7)×(0.105)³ 

= 0.004851 m³

Therefore, the volume of the ball = 0.004851 m³

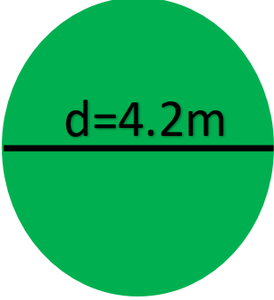
问题3：金属球的直径为4.2厘米。如果金属的密度为8.9 g / cm ³ ，那么球的质量是多少? (假设π = 22/7)

解决方案：

Given: Diameter of a metallic ball = 4.2 cm

Therefore, the radius of the metallic ball, r = 4.2/2 cm = 2.1 cm

By using the formula, volume of the metallic ball = 4/3 πr³

= (4/3)×(22/7)×(2.1)³ 

= 38.808 cm³

Now by using the relationship between, density, mass, and volume,

Density = Mass/Volume

Mass = Density × volume

= (8.9×38.808) g

= 345.3912 g

Therefore, the mass of the ball is 345.39 g (approx.)

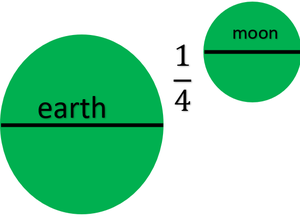
问题4：月亮的直径大约是地球直径的四分之一。月球的体积占地球体积的百分之几?

解决方案：

Let us assume the diameter of the earth as “d”. 

Therefore, the radius of the earth will be d/2

The diameter of the moon will be d/4 

The radius of the moon will be d/8

Finding the volume of the moon.

By using the formula, volume of the moon = (4/3) πr³ 

= (4/3) π (d/8)³ 

= 4/3π(d³/512)

Finding the volume of the earth :

By using the formula, volume of the earth = (4/3) πr³

= (4/3) π (d/2)³ 

= 4/3π(d³/8)

The fraction of the volume of the earth to the volume of the moon

Volume of moon/volume of earth = 4/3π(d³/512)/4/3π(d³/8)

= 1/64

Therefore, the volume of moon is 1/64 ^th of the volume of earth.

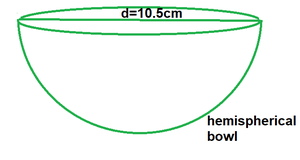
问题5：直径为10.5厘米的半球形碗可以容纳几升牛奶? (假设π = 22/7)

解决方案：

Given: Diameter of hemispherical bowl = 10.5 cm

Therefore, the radius of hemispherical bowl, r = 10.5/2 cm = 5.25 cm

By using the formula, volume of the hemispherical bowl = (2/3) πr³

= (2/3)×(22/7)×(5.25)³ 

= 303.1875 cm³

Therefore, the volume of the hemispherical bowl is 303.1875 cm³

Capacity of the bowl = (303.1875)/1000 L 

= 0.303 liters(approx.)

Therefore, the hemispherical bowl can hold 0.303 liters of milk.

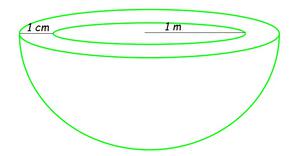
问题6：半球形的水箱由1厘米厚的铁皮制成。如果内半径为1 m，则找到用于制造水箱的铁的体积。 (假设π = 22/7)

解决方案：

Given: Inner Radius of the tank, (r) = 1m

Also, the thickness of hemispherical tank = 0.01m

Therefore, the outer Radius (R) = 1 + 0.01 = 1.01m

By using the formula, volume of the iron used in the tank = (2/3) π(R³– r³)

= (2/3)×(22/7) × (1.01³– 1³) 

= 0.06348 m³

Therefore, the volume of the iron used in the hemispherical tank is 0.06348 m³.

问题7：求出表面积为154 cm ²的球体的体积。 (假设π = 22/7)

解决方案：

Given: Surface area of sphere =154 cm²

Let us assume r to be the radius of a sphere.

By using the formula, Surface area of sphere = 4πr²

4πr² = 154 cm²

r² = (154×7)/(4 ×22)

r = 7/2

Radius r = 7/2 cm

Now,

By using the formula, volume of the sphere = (4/3) πr³

= (4/3)×(22/7)×(7/2)³

= 539/3 cm³

Therefore, the volume of a sphere is 539/3 cm³

问题8：建筑物的圆顶呈半球形。从内部将其粉刷成白色，价格为Rs。 4989.60。如果洗白的成本为每平方米Rs20，请找到

(i)圆顶的内表面积

(ii)圆顶内的空气量

(假设π= 22/7)

解决方案：

(i) Given: Cost of white-washing the dome from inside = Rs 4989.60

Also, Cost of white-washing 1m² area = Rs 20

Therefore, CSA of the inner side of dome = 498.96/2 m²  

= 249.48 m²

(ii) Let us assume the inner radius of the hemispherical dome be r.

CSA of the inner side of dome = 249.48 m²

By using the formula, CSA of a hemisphere = 2πr²

2πr² = 249.48

2×(22/7)×r² = 249.4

r² = (249.48×7)/(2×22)

r² = 39.6

r = 6.3

Hence, the radius r = 6.3 m

Volume of air inside the dome = Volume of hemispherical dome

By using the formula, volume of the hemisphere = 2/3 πr³

= (2/3)×(22/7)×(6.3)³

= 523.908 m³

= 523.9(approx.)

Therefore, the volume of air inside the dome is 523.9 m³.

问题9：半径为r和表面积为S的二十七个固态铁球被熔化，形成了表面积为S’的球。找出

(i)新球体的半径r’，

(ii)S与S’之比。

解决方案：

By using the formula, volume of the solid sphere = (4/3)πr³

Therefore, the volume of twenty-seven solid sphere = 27×(4/3)πr³ = 36 πr³

(i) Given: new solid iron sphere radius = r’

By using the formula, volume of this new sphere = (4/3)π(r’)³

(4/3)π(r’)³ = 36 πr³

(r’)³ = 27r³

r’= 3r

Radius of new sphere = 3r 

(ii) We know that,

Surface area of iron sphere of radius r, S =4πr²

Surface area of iron sphere of radius r’= 4π (r’)²

S/S’ = (4πr²)/( 4π(r’)²)

S/S’ = r²/(3r’)² 

= r²/9r²

= 1/9

Therefore, the ratio of S and S’ is 1: 9.

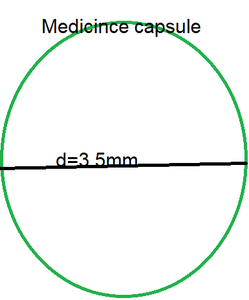
问题10：药物胶囊的直径为3.5毫米。填充此胶囊需要多少药物(以mm ^3计)? (假设π = 22/7)

解决方案：

Given: Diameter of capsule = 3.5 mm

Therefore, the radius of capsule, r = (3.5/2) mm = 1.75mm

By using the formula, volume of spherical capsule = 4/3 πr³

= (4/3)×(22/7)×(1.75)³ 

= 22.458 mm³

Therefore, the volume of the spherical capsule is 22.46 mm³.