偶数和奇数的子序列数

给定一个数组，求和为偶数的子序列的数量和和为奇数的子序列的数量。

例子：

Input: arr[] = {1, 2, 2, 3} 
Output: EvenSum = 7, OddSum = 8 
There are $2^{N}-1$possible subsequences. 
The subsequences with even sum is 
1) {1, 3} Sum = 4 
2) {1, 2, 2, 3} Sum = 8 
3) {1, 2, 3} Sum = 6 (Of index 1) 
4) {1, 2, 3} Sum = 6 (Of index 2) 
5) {2} Sum = 2 (Of index 1) 
6) {2, 2} Sum = 4 
7) {2} Sum = 2 (Of index 2) 
and the rest subsequence is of odd sum.

Input: arr[] = { 2, 2, 2, 2 } 
Output: EvenSum = 15, OddSum = 0  

天真的方法：
一种简单的方法是递归地生成所有可能的子序列，并计算具有偶数和的子序列的数量，然后从总子序列中减去，该数量将是奇数子序列。这种方法的时间复杂度为$O(2^{N})$ .

更好的方法：
更好的方法是使用动态编程。

• 当我们遍历数组时，我们将计算偶数子序列的计数。我们创建了 2 个数组 countODD[N] 和 countEVEN[N]，其中 countODD[i] 表示奇数和在范围内的子序列的数量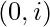$(0, i)$和 countEVEN[i] 表示范围内具有偶数和的子序列的数量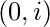$(0, i)$
• 如果我们在位置 i，并且数量是奇数，那么具有偶数和的子序列的总数将是
  • 对于countEVEN[i] ，第 i 个数字不与任何其他子序列配对(即偶数子序列直到$(i-1)$ position) +第 i 个数字与所有其他奇数子序列配对，直到$(i-1)$位置(奇数+奇数=偶数)
  • 对于countODD[i] ，第 i 个数字不与任何其他子序列(即奇数子序列，直到$(i-1)$ position) +第 i 个数字与所有其他偶数子序列配对，直到$(i-1)$位置 (odd+even=odd) +一个只有 1 个元素的子序列，即第 i 个数字本身
• 如果我们在位置 i，并且数量是偶数，那么具有偶数和的子序列的总数将是
  • 对于countEVEN[i] ，第 i 个数字不与任何其他子序列配对(即偶数子序列直到$(i-1)$ position) + 第i 个数字与所有其他偶数子序列配对，直到$(i-1)$位置 (even+even=even) +一个只有 1 个元素的子序列，即第 i 个数字本身
  • 对于countODD[i] ，第 i 个数字不与任何其他子序列配对(即奇数子序列直到$(i-1)$ position) + 第i 个数字与所有其他奇数子序列配对，直到$(i-1)$位置(偶数+奇数=奇数)

下面是上述方法的实现：

C++

// C++ implementation
#include 
using namespace std;
 
// returns the count of odd and
// even subsequences
pair countSum(int arr[], int n)
{
    int result = 0;
 
    // Arrays to store the count of even
    // subsequences and odd subsequences
    int countODD[n + 1], countEVEN[n + 1];
 
    // Initialising countEVEN[0] and countODD[0] to 0
    // since as there is no subsequence before the
    // iteration with even or odd count.
    countODD[0] = 0;
    countEVEN[0] = 0;
 
    // Find sum of all subsequences with even count
    // and odd count storing them as we iterate.
 
    // Here countEVEN[i] denotes count of
    // even subsequences till i
 
    // Here countODD[i] denotes count of
    // odd subsequences till i
 
    for (int i = 1; i <= n; i++) {
 
        // if the number is even
        if (arr[i - 1] % 2 == 0) {
            countEVEN[i] = countEVEN[i - 1]
                           + countEVEN[i - 1] + 1;
 
            countODD[i] = countODD[i - 1]
                          + countODD[i - 1];
        }
        // if the number is odd
        else {
            countEVEN[i] = countEVEN[i - 1]
                           + countODD[i - 1];
 
            countODD[i] = countODD[i - 1]
                          + countEVEN[i - 1] + 1;
        }
    }
 
    return { countEVEN[n], countODD[n] };
}
 
// Driver code
int main()
{
    int arr[] = { 1, 2, 2, 3 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Calling the function
 
    pair ans = countSum(arr, n);
 
    cout << "EvenSum = " << ans.first;
    cout << " OddSum = " << ans.second;
 
    return 0;
}

Java

// Java implementation to find the number
// of Subsequences with Even and Odd Sum
import java.util.*;
import java.lang.*;
 
class GFG
{
    public static int[] countSum(int arr[], int n)
    {
        int result = 0;
 
        // Arrays to store the count of even
        // subsequences and odd subsequences
        int[] countODD = new int[n + 1];
        int[] countEVEN = new int[n + 1];
         
        // Initialising countEVEN[0] and countODD[0] to 0
        // since as there is no subsequence before the
        // iteration with even or odd count.
        countODD[0] = 0;
        countEVEN[0] = 0;
         
        // Find sum of all subsequences with even count
        // and odd count storing them as we iterate.
     
        // Here countEVEN[i] denotes count of
        // even subsequences till i
     
        // Here countODD[i] denotes count of
        // odd subsequences till i
        for (int i = 1; i <= n; i++)
        {
 
            // if the number is even
            if (arr[i - 1] % 2 == 0)
            {
                countEVEN[i] = countEVEN[i - 1] +
                               countEVEN[i - 1] + 1;
     
                countODD[i] = countODD[i - 1] +
                              countODD[i - 1];
            }
             
            // if the number is odd
            else
            {
                countEVEN[i] = countEVEN[i - 1] +
                               countODD[i - 1];
     
                countODD[i] = countODD[i - 1] +
                              countEVEN[i - 1] + 1;
            }
        }
         
        int[] ans = new int[2];
        ans[0] = countEVEN[n];
        ans[1] = countODD[n];
        return ans;
    }
 
    // Driver Code
    public static void main (String[] args)
    {
        int[] arr = new int[]{ 1, 2, 2, 3 };
        int n = 4;
        int[] ans = countSum(arr, n);
        System.out.println("EvenSum = " + ans[0]);
        System.out.println("OddSum = " + ans[1]);
    }
}
 
// This code is contributed by Shivam Sharma

Python3

# Python3 implementation of above approach
 
# Returns the count of odd and
# even subsequences
def countSum(arr, n):
     
    result = 0
 
    # Variables to store the count of even
    # subsequences and odd subsequences
 
    # Initialising count_even and count_odd to 0
    # since as there is no subsequence before the
    # iteration with even or odd count.
    count_odd = 0
    count_even = 0
 
    # Find sum of all subsequences with even count
    # and odd count and storing them as we iterate.
 
    for i in range(n):
 
        # if the number is even
        if arr[i - 1] % 2 == 0:
            count_even = count_even + count_even + 1
            count_odd = count_odd + count_odd
 
        # if the number is odd
        else:
            temp = count_even
            count_even = count_even + count_odd
            count_odd = count_odd + temp + 1
         
    return [count_even, count_odd]
 
# Driver code
arr = [ 1, 2, 2, 3 ]
n = len(arr)
 
# Calling the function
ans = countSum(arr, n)
 
print('EvenSum =', ans[0],
      'OddSum =', ans[1])
 
# This code is contributed
# by Saurabh_shukla

C#

// C# implementation to find the number
// of Subsequences with Even and Odd Sum
using System;
class GFG
{
    public static int[] countSum(int []arr, int n)
    {
 
        // Arrays to store the count of even
        // subsequences and odd subsequences
        int[] countODD = new int[n + 1];
        int[] countEVEN = new int[n + 1];
         
        // Initialising countEVEN[0] and countODD[0] to 0
        // since as there is no subsequence before the
        // iteration with even or odd count.
        countODD[0] = 0;
        countEVEN[0] = 0;
         
        // Find sum of all subsequences with even count
        // and odd count storing them as we iterate.
     
        // Here countEVEN[i] denotes count of
        // even subsequences till i
     
        // Here countODD[i] denotes count of
        // odd subsequences till i
        for (int i = 1; i <= n; i++)
        {
 
            // if the number is even
            if (arr[i - 1] % 2 == 0)
            {
                countEVEN[i] = countEVEN[i - 1] +
                               countEVEN[i - 1] + 1;
     
                countODD[i] = countODD[i - 1] +
                              countODD[i - 1];
            }
             
            // if the number is odd
            else
            {
                countEVEN[i] = countEVEN[i - 1] +
                               countODD[i - 1];
     
                countODD[i] = countODD[i - 1] +
                              countEVEN[i - 1] + 1;
            }
        }
         
        int[] ans = new int[2];
        ans[0] = countEVEN[n];
        ans[1] = countODD[n];
        return ans;
    }
 
    // Driver Code
    public static void Main (String[] args)
    {
        int[] arr = new int[]{ 1, 2, 2, 3 };
        int n = 4;
        int[] ans = countSum(arr, n);
        Console.WriteLine("EvenSum = " + ans[0]);
        Console.WriteLine("OddSum = " + ans[1]);
    }
}
 
// This code is contributed by Rajput-Ji

Javascript

  
// JavaScript implementation to find the number
// of Subsequences with Even and Odd Sum
function countSum(arr, n)
{
    // Arrays to store the count of even
    // subsequences and odd subsequences
    var countODD = Array(n+1).fill(0);
    var countEVEN = Array(n+1).fill(0);
     
    // Initialising countEVEN[0] and countODD[0] to 0
    // since as there is no subsequence before the
    // iteration with even or odd count.
    countODD[0] = 0;
    countEVEN[0] = 0;
     
    // Find sum of all subsequences with even count
    // and odd count storing them as we iterate.
 
    // Here countEVEN[i] denotes count of
    // even subsequences till i
 
    // Here countODD[i] denotes count of
    // odd subsequences till i
    for (var i = 1; i <= n; i++)
    {
        // if the number is even
        if (arr[i - 1] % 2 == 0)
        {
            countEVEN[i] = countEVEN[i - 1] +
                           countEVEN[i - 1] + 1;
 
            countODD[i] = countODD[i - 1] +
                          countODD[i - 1];
        }
         
        // if the number is odd
        else
        {
            countEVEN[i] = countEVEN[i - 1] +
                           countODD[i - 1];
 
            countODD[i] = countODD[i - 1] +
                          countEVEN[i - 1] + 1;
        }
    }
     
    var ans = [0,0];
    ans[0] = countEVEN[n];
    ans[1] = countODD[n];
    return ans;
}
// Driver Code
var arr = [ 1, 2, 2, 3 ];
var n = 4;
var ans = countSum(arr, n);
document.write("EvenSum = " + ans[0]);
document.write(" OddSum = " + ans[1]);
 
 

输出：

EvenSum = 7 OddSum = 8

时间复杂度：O(N) 。
空间复杂度：O(N) ，其中 N 是数组中元素的数量。

有效的方法：
与创建 countEVEN[N] 和 countODD[N] 数组不同，我们只需要 count_even 变量和 count_odd 变量，并像之前一样更改它。
下面是上述方法的实现：

C++

// C++ implementation
#include 
using namespace std;
 
// Returns the count of odd and
// even subsequences
pair countSum(int arr[], int n)
{
    int result = 0;
 
    // Variables to store the count of even
    // subsequences and odd subsequences
    int count_odd, count_even;
 
    // Initialising count_even and count_odd to 0
    // since as there is no subsequence before the
    // iteration with even or odd count.
    count_odd = 0;
    count_even = 0;
 
    // Find sum of all subsequences with even count
    // and odd count and storing them as we iterate.
 
    for (int i = 1; i <= n; i++) {
 
        // if the number is even
        if (arr[i - 1] % 2 == 0) {
            count_even = count_even + count_even + 1;
            count_odd = count_odd + count_odd;
        }
 
        // if the number is odd
        else {
            int temp = count_even;
            count_even = count_even + count_odd;
            count_odd = count_odd + temp + 1;
        }
    }
 
    return { count_even, count_odd };
}
 
// Driver code
int main()
{
    int arr[] = { 1, 2, 2, 3 };
    int n = sizeof(arr) / sizeof(arr[0]);
 
    // Calling the function
 
    pair ans = countSum(arr, n);
 
    cout << "EvenSum = " << ans.first;
    cout << " OddSum = " << ans.second;
 
    return 0;
}

Java

// Java program to get minimum cost to sort
// strings by reversal operation
class GFG
{
 
static class pair
{
    int first, second;
    public pair(int first, int second)
    {
        this.first = first;
        this.second = second;
    }
}
 
// Returns the count of odd and
// even subsequences
static pair countSum(int arr[], int n)
{
    int result = 0;
 
    // Variables to store the count of even
    // subsequences and odd subsequences
    int count_odd, count_even;
 
    // Initialising count_even and count_odd to 0
    // since as there is no subsequence before the
    // iteration with even or odd count.
    count_odd = 0;
    count_even = 0;
 
    // Find sum of all subsequences with even count
    // and odd count and storing them as we iterate.
    for (int i = 1; i <= n; i++)
    {
 
        // if the number is even
        if (arr[i - 1] % 2 == 0)
        {
            count_even = count_even + count_even + 1;
            count_odd = count_odd + count_odd;
        }
 
        // if the number is odd
        else
        {
            int temp = count_even;
            count_even = count_even + count_odd;
            count_odd = count_odd + temp + 1;
        }
    }
    return new pair(count_even, count_odd );
}
 
// Driver code
public static void main(String[] args)
{
    int arr[] = { 1, 2, 2, 3 };
    int n = arr.length;
 
    // Calling the function
 
    pair ans = countSum(arr, n);
 
    System.out.print("EvenSum = " + ans.first);
    System.out.print(" OddSum = " + ans.second);
}
}
 
// This code is contributed by 29AjayKumar

蟒蛇3

# Python3 implementation of above approach
 
# Returns the count of odd and
# even subsequences
def countSum(arr, n):
    result = 0
     
    # Variables to store the count of even
    # subsequences and odd subsequences
    # Initialising count_even and count_odd to 0
    # since as there is no subsequence before the
    # iteration with even or odd count.
    count_odd = 0
    count_even = 0
 
    # Find sum of all subsequences with even count
    # and odd count and storing them as we iterate.
 
    for i in range(1, n + 1):
         
        # if the number is even
        if (arr[i - 1] % 2 == 0):
            count_even = count_even + count_even + 1
            count_odd = count_odd + count_odd
 
        # if the number is odd
        else:
            temp = count_even
            count_even = count_even + count_odd
            count_odd = count_odd + temp + 1
 
    return (count_even, count_odd)
     
# Driver code
arr = [1, 2, 2, 3];
n = len(arr)
 
# Calling the function
count_even, count_odd = countSum(arr, n);
 
print("EvenSum = ", count_even,
      " OddSum = ", count_odd)
       
# This code is contributed
# by ANKITKUMAR34

C＃

// C# program to get minimum cost to sort
// strings by reversal operation
using System;
     
class GFG
{
 
public class pair
{
    public int first, second;
    public pair(int first, int second)
    {
        this.first = first;
        this.second = second;
    }
}
 
// Returns the count of odd and
// even subsequences
static pair countSum(int []arr, int n)
{
    // Variables to store the count of even
    // subsequences and odd subsequences
    int count_odd, count_even;
 
    // Initialising count_even and count_odd to 0
    // since as there is no subsequence before the
    // iteration with even or odd count.
    count_odd = 0;
    count_even = 0;
 
    // Find sum of all subsequences with even count
    // and odd count and storing them as we iterate.
    for (int i = 1; i <= n; i++)
    {
 
        // if the number is even
        if (arr[i - 1] % 2 == 0)
        {
            count_even = count_even + count_even + 1;
            count_odd = count_odd + count_odd;
        }
 
        // if the number is odd
        else
        {
            int temp = count_even;
            count_even = count_even + count_odd;
            count_odd = count_odd + temp + 1;
        }
    }
    return new pair(count_even, count_odd );
}
 
// Driver code
public static void Main(String[] args)
{
    int []arr = { 1, 2, 2, 3 };
    int n = arr.Length;
 
    // Calling the function
 
    pair ans = countSum(arr, n);
 
    Console.Write("EvenSum = " + ans.first);
    Console.Write(" OddSum = " + ans.second);
}
}
 
// This code is contributed by PrinciRaj1992

Javascript

 
// Java program to get minimum cost to sort
// strings by reversal operation
var first, second;
function pair( first,  second)
{
    this.first = first;
    this.second = second;
}
 
// Returns the count of odd and
// even subsequences
function countSum(arr, n)
{
    var result = 0;
 
    // Variables to store the count of even
    // subsequences and odd subsequences
    var count_odd, count_even;
 
    // Initialising count_even and count_odd to 0
    // since as there is no subsequence before the
    // iteration with even or odd count.
    count_odd = 0;
    count_even = 0;
 
    // Find sum of all subsequences with even count
    // and odd count and storing them as we iterate.
    for (var i = 1; i <= n; i++)
    {
 
        // if the number is even
        if (arr[i - 1] % 2 == 0)
        {
            count_even = count_even + count_even + 1;
            count_odd = count_odd + count_odd;
        }
 
        // if the number is odd
        else
        {
            var temp = count_even;
            count_even = count_even + count_odd;
            count_odd = count_odd + temp + 1;
        }
    }
    return new pair(count_even, count_odd );
}
 
// Driver code
var arr = [ 1, 2, 2, 3 ];
var n = arr.length;
 
// Calling the function
 
var ans = countSum(arr, n);
 
document.write("EvenSum = " + ans.first);
document.write(" OddSum = " + ans.second);
 
// This code is contributed by shivanisinghss2110
 

输出：

EvenSum = 7 OddSum = 8

时间复杂度：O(N) 。
空间复杂度： O(1) ，其中 N 是数组中的元素数。

如果您希望与专家一起参加现场课程，请参阅DSA 现场工作专业课程和学生竞争性编程现场课程。