Logistic 回归的优缺点

逻辑回归是一种分类算法，用于寻找事件成功和事件失败的概率。当因变量本质上是二进制（0/1，真/假，是/否）时使用它。它支持通过研究给定标记数据集的关系将数据分类为离散类。它从给定的数据集中学习线性关系，然后以 Sigmoid函数的形式引入非线性。

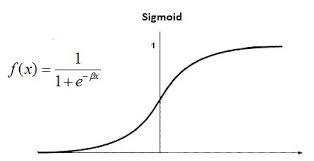
逻辑回归也称为二项式逻辑回归。它基于 sigmoid函数，其中输出是概率，输入可以从 -无穷大到 +无穷大。让我们讨论一下线性回归的一些优点和缺点。

Advantages	Disadvantages
Logistic regression is easier to implement, interpret, and very efficient to train.	If the number of observations is lesser than the number of features, Logistic Regression should not be used, otherwise, it may lead to overfitting.
It makes no assumptions about distributions of classes in feature space.	It constructs linear boundaries.
It can easily extend to multiple classes(multinomial regression) and a natural probabilistic view of class predictions.	The major limitation of Logistic Regression is the assumption of linearity between the dependent variable and the independent variables.
It not only provides a measure of how appropriate a predictor(coefficient size)is, but also its direction of association (positive or negative).	It can only be used to predict discrete functions. Hence, the dependent variable of Logistic Regression is bound to the discrete number set.
It is very fast at classifying unknown records.	Non-linear problems can’t be solved with logistic regression because it has a linear decision surface. Linearly separable data is rarely found in real-world scenarios.
Good accuracy for many simple data sets and it performs well when the dataset is linearly separable.	Logistic Regression requires average or no multicollinearity between independent variables.
It can interpret model coefficients as indicators of feature importance.	It is tough to obtain complex relationships using logistic regression. More powerful and compact algorithms such as Neural Networks can easily outperform this algorithm.
Logistic regression is less inclined to over-fitting but it can overfit in high dimensional datasets.One may consider Regularization (L1 and L2) techniques to avoid over-fittingin these scenarios.	In Linear Regression independent and dependent variables are related linearly. But Logistic Regression needs that independent variables are linearly related to the log odds (log(p/(1-p)).