线性映射
线性映射
设 V 和 W 是域 K 上的向量空间。函数f: V-> W 被称为两个向量 v,u 的线性映射![]() 和一个标量 c \
和一个标量 c \ ![]() 克:
克:
- 如果转换本质上是加法的:
![]()
- 如果它们在标量方面本质上是乘法的。
![]()
零/身份转换
线性变换从向量空间到自身称为线性运算符:
- 零转换:对于转换
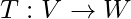 如果满足以下条件,则称为零变换:
如果满足以下条件,则称为零变换:
![]()
- 身份转换:对于转换
如果满足以下条件,则称为身份转换:
![]()
线性变换的性质
令 T: V \rightarrow W 为线性变换,其中 u,v \epsilon V。那么,以下性质为真:
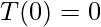
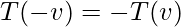
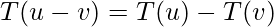
- 如果
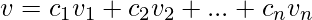 然后,
然后, 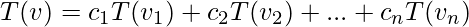
矩阵的线性变换
令 T 为 mxn 矩阵,变换 T: ![]() 是线性变换,如果:
是线性变换,如果:
![]()
零和单位矩阵操作
- 矩阵 mxn 矩阵是一个零矩阵,对应于从 R^n \rightarrow R^m 的零变换。
- 矩阵 nxn 矩阵是单位矩阵
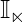 , 对应于从零变换
, 对应于从零变换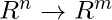 .
.

例子
让我们考虑从 R^{2} \rightarrow R^3 的线性变换,使得:
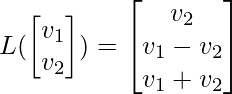
现在,我们将验证它是一个线性变换。为此,我们需要检查线性映射的上述两个条件,首先,我们将检查常数乘法条件:
![]()
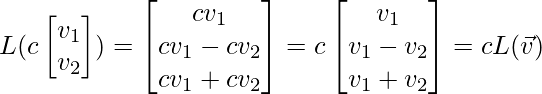
以及以下转换:
![]()
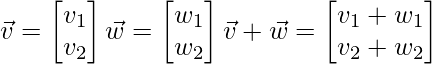
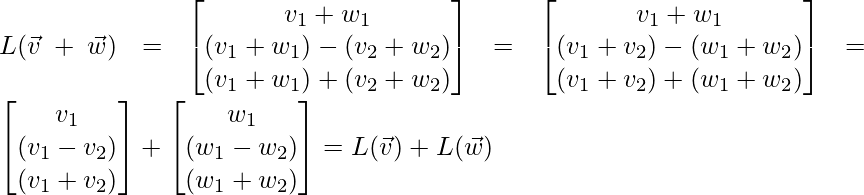
证明上述变换是线性变换。非线性变换的示例包括三角变换、多项式变换。
内核/范围空间:
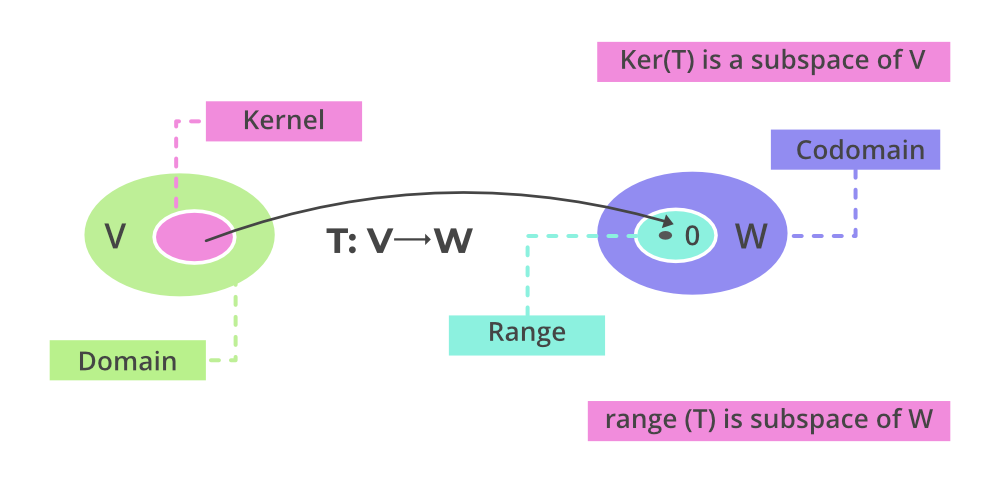
内核空间:
令 T: V \rightarrow W 是线性变换,然后 \forall v \epsilon V 使得:
![]()
是 T 的核空间。也称为 T 的零空间。
- T:V \rightarrow W 的零变换核空间是 W。
- T:V \rightarrow W 的恒等变换的核空间是 {0}。
内核空间的维度称为 nullity 或 null(T)。
范围空间:
令 T: V \rightarrow W 是线性变换,然后 \forall v \epsilon V 使得:
![]()
是 T 的范围空间。对于矩阵的线性变换,范围空间总是非空集,因为:
![]()
范围空间的维度称为秩 (T)。 rank 和 nullity 的总和是域的维度:
![]()
作为旋转的线性变换
当应用于某个向量时,一些变换运算符给出向量的输出,该向量以原始向量的角度θ旋转。
- 线性变换 T: R^2 \rightarrow R^2 由矩阵给出:
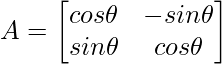 具有将每个向量逆时针围绕原点 wrt 角 \theta 旋转的特性:
具有将每个向量逆时针围绕原点 wrt 角 \theta 旋转的特性:
让 v 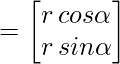
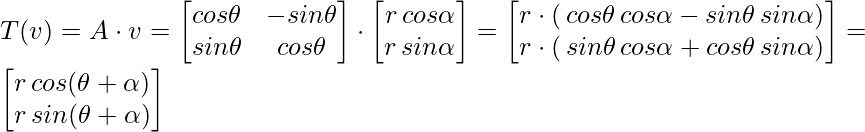
这类似于将原始向量旋转 \theta。
作为投影的线性变换
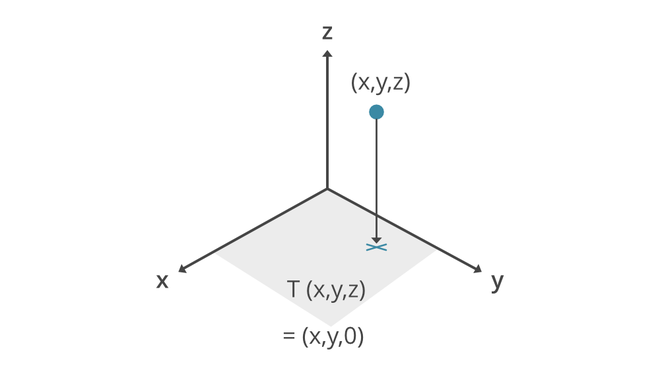
线性变换 T: R^3 \rightarrow R^3 由下式给出:
T = 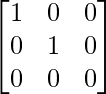
如果向量由 v = (x, y, z) 给出。那么,T\cdot v = (x, y, 0)。即原向量的正交投影。
微分作为线性变换
让 T: ![]() 是微分变换,使得:
是微分变换,使得: ![]() 然后对于两个多项式 p(z),
然后对于两个多项式 p(z), ![]() , 我们有:
, 我们有:
![]()
同样,对于标量 a \epsilon F,我们有:
![]()
上式证明微分是线性变换。
参考:
- 线性变换幻灯片