TCS安置纸| MCQ 8

这是用于能力倾向准备的TCS模型放置论文。这份安置文件将涵盖在TCS招聘活动中提出的才能问题，并且还将严格遵循在TCS面试中提出的问题模式。建议解决以下每个问题，以增加清除TCS面试的机会。

1. 确定序列中缺少的数字：2、5，__，19、37、75?
   a)16
   b)12
   c)10
   d)9

   Answer: d) 9

   Solution:
   2 * 2 + 1 = 5
   5 * 2 – 1 = 9
   9 * 2 + 1 = 19
   19 * 2 – 1 = 37 and so on

2. 矩形分为面积分别为70、36、20和x的四个矩形。 ‘x’的值是多少?
   
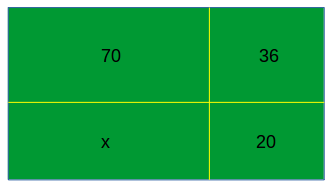
   a)350/7
   b)350/11
   c)350/9
   d)350/13

   Answer: c) 350/9

   Solution:
   Since the areas of the rectangles are in proportion we can say,
   => 70/x = 36/20
   => x = 350/9

3. 如果VXUPLVH编写为SURMISE，那么SHDVD编写为什么?
   a)PEASA
   b)PBASA
   c)PEBSB
   d)以上都不是

   Answer: a) PEASA

   Solution:
   It is a question of coding-decoding where,
   V is written as S (V – 3 = S)
   X is written as U (X – 3 = U)
   and so on.
   Similarly, SHDVD will be written as PEASA

4. Aman欠Bipul 50卢比。他同意从星期一开始连续多个天向Bipul支付，每天支付10卢比或20卢比的单笔票据。阿曼可以通过多种方式偿还比普尔。 (如果至少有一天，则给出了两种不同面额的注释，这两种方法被认为是不同的)
   a)5
   b)6
   c)7
   d)8

   Answer: d) 8

   Solution:
   Aman can pay Bipul in all 10 rupees note in 5 days = 5 * 10 = 50 rupees = 1 way
   Aman can pay Bipul in 3 ten rupee note and 1 twenty rupee note = 4!/(3! * 1!) = 4 ways
   Aman can pay Bipul in 1 ten rupee note and 2 twenty rupee note = 3!/(1! * 2!) = 3 ways
   So in all Aman can pay Bipul in 8 ways.

5. 萨利姆(Salim)以27卢比的价格购买了一定数量的橙色，价格为M的2倍卢比，其中M为整数。他将这些橙子分成相等的两半，一部分以M卢比以13橙的价格出售，以M卢比以14橙的价格出售。他花了整整卢比，没有卢比，但买了最少数量的橘子。他买了多少?
   a)980
   b)9828
   c)1880年
   d)102660

   Answer: b) 9828

   Solution:
   Let Salim buy 2x number of oranges.
   So he buys 27 oranges at a price of 2M.
   He buys 1 orange at a price of 2M/27
   or, x oranges cost him Rs. 2Mx/27
   Now he sells x oranges at the rate of 13 oranges for Rs. M
   So he sells 1 orange at Rs. M/13
   and x oranges at Rs Mx/13
   Same goes for 14 oranges which are Mx/14,
   According to the question, 2Mx/27, Mx/13, Mx/14 are integers
   So, x oranges must be divisible by 27, 13 and 14
   The lcm of 27, 13 and 14 = 4914 or 2x = 9828

6. 在足球比赛中，有16支球队参加，并分为4组。每个小组中的每个团队将互相比赛一次。排名前2的获胜球队将进入下一轮比赛，因此排名前2的前两支球队将参加决赛。那么在那场比赛中将参加多少场最低比赛?
   a)40
   b)14
   c)43
   d)50

   Answer: c) 43

   Solution:
   Total matches to be played = 4C2 = 6 matches.
   So total number of matches played in the first round = 6 * 4 = 24 matches
   Now top two teams from each group progress to the next round. These 8 teams are to be divided into 2 groups.
   Total matches played in the second round = 6 × 2 = 12 matches
   Now 4 teams progress to the next round. Total matches played in the third round = 6 * 1 = 6matches
   From this round, 2 teams progress to the next round. And final will be played between them.
   Total matches = 24 + 12 + 6 + 1 = 43

7. 有12个字母和正好12个信封。每个信封中随机插入一个字母。在不正确的信封中准确插入1个字母的概率是多少?
   a)1
   b)0
   c)10！
   d)这些都不是

   Answer: b) 0

   Solution:
   This is a question of very common sense in which,
   12 letters are to be inserted in 12 envelopes, 1 in each, so if one letter is inserted into a wrong envelope there has to be another letter which is to be inserted into another wrong envelope. So the probability of this is 0.

8. 地面上的中空空间将被填充。填充的总成本为Rs。 20000。每立方米的填充成本为225卢比。填充空心空间所需的3立方米土壤大小是多少倍?
   a)29.62
   b)30.32
   c)88.88
   d)43.64

   Answer: a) 29.62

   Solution:
   The total cost of filling = 20, 000
   Cost of filling 1 cubic meter = Rs. 225
   So cubic meters to be filled = 20, 000/225 = 88.89 meter-cube
   Now we need to find the three times of 88.89 to be filled = 88.89/3 = 29.63
   So the closest match is 29.62

9. 7位数字由所有不同的数字组成。如果将最右边和最左边的数字分别固定为5和6，那么可以找到多少个这样的数字?
   a)120
   b)30240
   c)6720
   d)这些都不是

   Answer: c) 6720

   Solution:
   If the digits at extreme left and right are fixed as 5 and 6, then the number of digits left = 8
   So the in-between 5 places can be filled in 8 * 7 * 6 * 5 * 4 ways
   = 6720 ways

10. 轿车中有五个轮胎(四个公路轮胎和一个备用轮胎)在行驶40,000公里的过程中将被平均使用。每个轮胎的使用公里数为
    a)32000
    b)8000
    c)4000
    d)10000

    Answer: a) 32000

    Solution:
    The total km travelled by the sedan = 40, 000 km
    Since every tire capacity’s = 40, 000/5 = 8000 km each
    So total distance covered by each tire = 8000*4 = 32000 km each will be travelled by each tire after being worn out after every 8000 km.