问题13 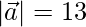 ,
, 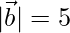 和
和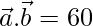 , 找
, 找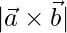
解决方案:
We know that,
=> ![]()
=>![]()
=> ![]()
=> ![]()
=>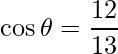
Also,
=>![]()
And ![]()
=> ![]()
=> 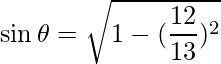
=> 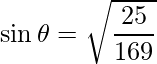
=> 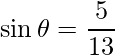
=> 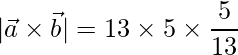
=>![]()
问题14:找到2个向量之间的角度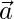 和
和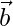 , 如果
, 如果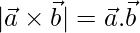
解决方案:
Given ![]()
=>![]()
=>![]() , as
, as ![]() is a unit vector.
is a unit vector.
=> ![]()
=> ![]()
=> ![]()
问题15  ,然后证明
,然后证明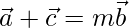 ,其中m是任何标量。
,其中m是任何标量。
解决方案:
Given that ![]()
=> ![]()
=> ![]()
=>![]()
Using distributive property,
=> ![]()
If two vectors are parallel, then their cross-product is 0 vector.
=> ![]() and
and ![]() are parallel vectors.
are parallel vectors.
=> ![]()
Hence proved.
问题16:如果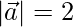 ,
, 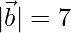 和
和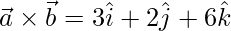 ,找出两者之间的夹角
,找出两者之间的夹角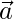 和
和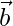
解决方案:
Given that,![]() ,
, ![]() and
and ![]()
We know that,
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> 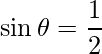
=> ![]()
问题17:如果可以得出什么推论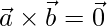 和
和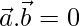
解决方案:
Given, ![]() and
and ![]()
=>![]()
=>![]()
Either of the following conditions is true,
1.![]()
2. ![]()
3. ![]()
4.![]() is parallel to
is parallel to ![]()
=> ![]()
=> ![]()
Either of the following conditions is true,
1. ![]()
2.![]()
3. ![]()
4. ![]() is perpendicular to
is perpendicular to ![]()
Since both these conditions are true, that implies atleast one of the following conditions is true,
1. ![]()
2. ![]()
3. ![]()
问题18  ,
,  和
和 是3个单位向量
是3个单位向量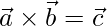 ,
, 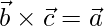 和
和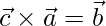 。显示
。显示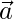 ,
, 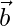 和
和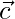 形成单位向量的正交右手三合会。
形成单位向量的正交右手三合会。
解决方案:
Given, ![]() ,
, ![]() and
and ![]()
As,
=>![]()
=> ![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]() .
.
Similarly,
=> ![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]()
=> ![]() is perpendicular to both
is perpendicular to both ![]() and
and ![]()
=> ![]() ,
, ![]() and
and ![]() are mutually perpendicular.
are mutually perpendicular.
As, ![]() ,
, ![]() and
and ![]() are also unit vectors,
are also unit vectors,
=> ![]() ,
, ![]() and
and ![]() form an orthogonal right-handed triad of unit vectors
form an orthogonal right-handed triad of unit vectors
Hence proved.
问题19.找到一个垂直于平面ABC的单位矢量,其中A,B和C的坐标为A(3,-1,2),B(1,-1,3)和C(4,- 3,1)。
解决方案:
Given A(3, -1, 2), B(1, -1, 3) and C(4, -3, 1).
Let,
=> ![]()
=> ![]()
=> ![]()
Plane ABC has two vectors ![]() and
and ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
A vector perpendicular to both ![]() and
and ![]() is given by,
is given by,
=> 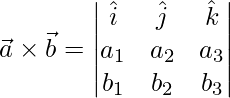
=> 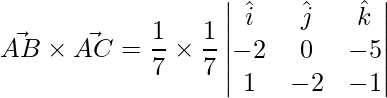
=> ![Rendered by QuickLaTeX.com \vec{AB}\times\vec{AC} = \hat{i}[(0)(-1)-(-2)(-5)] -\hat{j}[(-2)(-1)-(1)(-5)] +\hat{k}[(-2)(-2)-(1)(0)]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2025%20Vector%20or%20Cross%20Product%20%E2%80%93%20Exercise%2025.1%20%7C%20Set%202_122.jpg)
=> ![]()
=>![]()
To find the unit vector,
=> 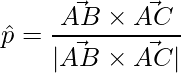
=> 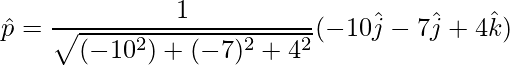
=> 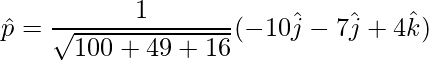
=> 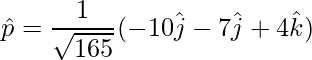
问题20.如果a,b和c是三角形ABC的边BC,CA和AB的长度,则证明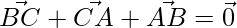 并推断出
并推断出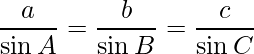
解决方案:
Given that ![]() ,
, ![]() and
and ![]()
From triangle law of vector addition, we have
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=>![]()
=> ![]()
=> 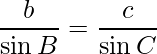
Similarly,
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=> ![]()
=>![]()
=> ![]()
=> ![]()
=> ![]()
=> 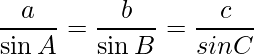
Hence proved.
问题21.如果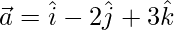 和
和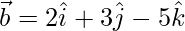 ,然后找到
,然后找到 。验证
。验证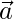 和
和 彼此垂直。
彼此垂直。
解决方案:
Given, ![]() and
and ![]()
=>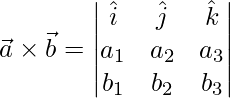
=>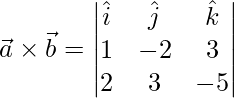
=> ![]()
=>![]()
=> ![]()
Two vectors are perpendicular if their dot product is zero.
=>![]()
=> ![]()
=> ![]()
=> ![]()
Hence proved.
问题22:如果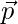 和
和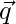 是形成一个角度的单位向量
是形成一个角度的单位向量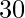 ,找到具有以下特征的平行四边形的面积:
,找到具有以下特征的平行四边形的面积: 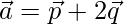 和
和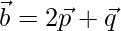 作为其对角线。
作为其对角线。
解决方案:
Given ![]() and
and ![]() forming an angle of
forming an angle of ![]() .
.
Area of a parallelogram having diagonals ![]() and
and ![]() is
is 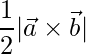
=> ![]()
=> 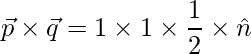
=>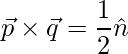
Thus area is,
=> Area = 
=> Area = 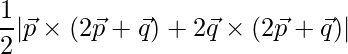
=> Area = 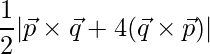
=> Area = 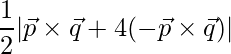
=> Area = 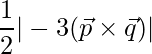
=> Area =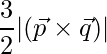
=> Area = 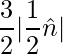
=> Area = 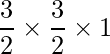
=> Area = ![]() square units
square units
问题23:对于任何两个向量 和
和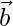 , 证明
, 证明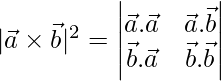
解决方案:
We know that,
=> ![]()
=>![]()
=>![]()
=>![]()
=> ![]()
=> ![]()
=> ![]()
=>![]()
=>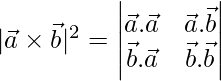
Hence proved.
问题24.定义 并证明
并证明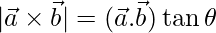 , 在哪里
, 在哪里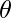 是之间的角度
是之间的角度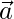 和
和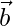
解决方案:
Definition of ![]() : Let
: Let ![]() and
and ![]() be 2 non-zero, non-parallel vectors. Then
be 2 non-zero, non-parallel vectors. Then ![]() , is defined as a vector with the magnitude of
, is defined as a vector with the magnitude of ![]() , and which is perpendicular to both the vectors
, and which is perpendicular to both the vectors ![]() and
and ![]() .
.
We know that,
=> ![]()
=> ![]()
=>![]() ……………..(eq.1)
……………..(eq.1)
And as,
=> ![]()
=>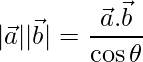
Substituting in (eq.1),
=> 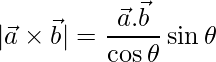
=> ![]()