第 11 类 RD Sharma 解决方案 - 第 25 章抛物线 - 练习 25.1 |设置 2

问题 11. 找出焦点为 (5, 2) 且顶点位于 (3, 2) 的抛物线方程。

解决方案：

Given that, the vertex of the parabola is (3, 2) and the focus of the parabola is (5, 2)

So, the slope of the axis of the parabola = 0

The slope of the directrix is not defined.

Let us assume the directrix intersect the axis at point K (r, s).  

So, (r + 5)/2 = 3, (s + 2)/2 = 2

=> r = 1, s = 2

Hence, the equation of the directrix is x – 1 = 0 or x = 1.

Now, let us assume P (x, y) be any point on the parabola whose focus is S (5, 2).

And the equation of directrix is x =1.

So, the first we draw PM perpendicular to x  = 1.

Then

SP = PM

SP² = PM²

(x – 5)² + (y – 2)² = $\left( \frac{x - 1}{1} \right)^2$

x² + 25 – 10x + y² + 4 – 4y = x² + 1 – 2x

25 – 10x + y² + 4 – 4y – 1 + 2x = 0

=> y² – 4y – 8x + 28 = 0

Hence, the equation of the parabola is y² – 4y – 8x + 28 = 0

问题 12. 均载悬索桥的索以抛物线形式悬挂。水平的 100 m 长的道路由连接在电缆上的垂直电线支撑，最长的电线为 30 m，最短的电线为 6 m。求距离中间 18 m 处连接到道路的支撑线的长度。

解决方案：

Given that the suspension cable forms a parabola with the vertex at (0, 6).

So, let us assume that the equation of the parabola formed by the suspension cable be,  

(x – 0)² = 4a (y – 6)

And it passes through point P (−50, 30) and Q (50, 30).  

So, 2500 = 4a (30 – 6)

=> 4a = 2500/24

By putting the value of 4a in the given equation, we get

x² = (2500/24) (y – 6)

Now, let the coordinates be (18, l) and it lies on the parabola (2).  

So, 18² = (2500/24) (l – 6)

=> 324 = (2500/24) (l – 6)

=> l = 9.11 m

Therefore, 9.11 m is the supporting wire attached to the roadway 18 m from the middle.

问题 13. 找出连接抛物线 y ² = 6x 的顶点到其上横坐标为 24 的点的直线方程。

解决方案：

Let us assume A and B be points on the parabola y² = 6x.

Now, OA, OB be the lines joining the vertex O to the points A and B whose abscissa is 24.  

Now,

=> y² = 6 × 24 

=> y² = 144

=> y = ± 12

So, the coordinates of the points A is (24, 12) and B is (24, –12).

Hence, the equation of lines are 

=> $y - 0 = \pm \frac{12 - 0}{24 - 0}(x - 0)$

=> ±2y = x

问题 14. 求抛物线上 y ² = 8x 焦距为 4 的点的坐标。

解决方案：

Given that, the parabola is y² = 8x 

⇒ y² = 4(2)x

Now, on comparing it with the general equation of parabola y² = 4ax, we will get a = 2.

Let us assume that the required point be (x₁, y₁).

Also, given that focal distance is 4

=> x₁ + a = 4

=> x₁ + 2 = 4

=> x₁ = 2

Now, this point satisfy the equation of parabola,

So, (y₁)² = 8(2) = 16

=> y₁² = 16

=> y₁ = ± 4

Hence, the coordinates of the points are (2, 4) and (2, −4).

问题 15. 求连接抛物线顶点 y ² = 4ax 的线段的长度和抛物线上的一点，线段与 x 轴成 θ 角。

解决方案：

Let us assume that the coordinates of the point on the parabola is B (x₁, y₁) and BO be the line segment in the parabola.

Now, in triangle AOB, 

cos θ = AO/OB and sin θ = AB/OB

=> cos θ = x₁/OB  and sin θ = y₁/OB

x₁ = OB cos θ and y₁ = OB sin θ

Now, the curve is passing through point (x₁, y₁)

So, (y₁)² = 4a(x₁)

=> (OB sin θ)² = 4a (OB cos θ)  

=> (OB)² sin2 θ = 4a OB cos θ

=> OB = 4a cos θ/sin² θ

=> OB = 4a cosec θ cot θ

Therefore, the required length is 4a cosec θ cot θ.

问题 16. 如果点 (0, 4) 和 (0, 2) 分别是抛物线的顶点和焦点，则求抛物线的方程。

解决方案：

Given that the vertex of the parabola is (0, 4) and the focus of the parabola is (0, 2)

From the points we conclude that the vertex and focus lie on y-axis, so y-axis is the axis of the parabola.

Now, if the directrix meets the axis of the parabola at point Z, then AZ = AF = 2.

OZ = OF + AZ + FA 

= 2 + 2 + 2 

= 6

So, the equation of the directrix is y = 6.

i.e., y − 6 = 0

Let us assume P(x, y) be any point in the plane of the focus and directrix. 

And MP be the perpendicular distance from P to the directrix, then P lies on parabola if FP = MP.

$\sqrt{\left( x - 0 \right)^2 + \left( y - 2 \right)^2} = \frac{\left| y - 6 \right|}{1}$

x² + y² – 4y + 4 = y² – 12y + 36

=> x² + 8y = 32

Hence, the equation of the parabola is x² + 8y = 32

问题 17. 如果直线 y = mx + 1 与抛物线 y ² = 4x 相切，则求 m 的值。

解决方案：

Given that the equation of the is y² = 4x.

On substituting the value of y = mx + 1 in the equation of parabola, we get

(mx + 1)² = 4x

⇒ m²x² + 2mx + 1 = 4x

⇒ m²x² + (2m − 4)x + 1 = 0           

As we know that a tangent touches the curve at a point, so the roots of the equation must be equal.

So, D = 0

=> (2m − 4)² − 4m² = 0

=> 4m² −16m + 16 − 4m² = 0

=> m = 1

Therefore, the value of m is 1.

问题 18. 求抛物线 y ² + 6y + 2x + 5 = 0 的顶点和焦点之间的距离。

解决方案：

Given that the equation of the parabola is y² + 6y + 2x + 5 = 0

(y + 3)² + 2x – 4 = 0

(y + 3)² = -2 (x – 2)

Let us assume Y = y + 3 and X = x – 2.

Now we get

Y² = – 2X

On putting 4a = 2, we get

=> a = 1/2

Focus = (X = -1/2, Y = 0) = (x = 3/2, y = – 3)

Vertex = (X = 0, Y = 0) = (x = 2, y = -3)

So, 

Focus = (3/2, -3)

Vertex = (2, -3)

Now, we find the distance between the vertex and the focus is,

D = $\sqrt{\left( \frac{3}{2} - 2 \right)^2 + \left( - 3 + 3 \right)^2}$

= $\sqrt{\left( \frac{1}{2} \right)^2}$

= 1/2 units

Therefore, the required distance is 1/2 units.

问题 19. 求抛物线 x ² − 4x − 8y + 12 = 0 的准线方程。

解决方案：

Given that the equation of the parabola is x² − 4x − 8y + 12 = 0  

(x – 2)² – 4 – 8y + 12 = 0

(x – 2)² = 8 (y – 1) 

Let us assume Y = y − 1 and X = x – 2. 

Now we get

X² = 8Y

Now, on comparing with x² = 4ay, we get

=> a = 2

So, Directrix = Y = −a

=> y − 1 = −a

=> y = −a + 1

=> y = −2 + 1

=> y = −1  

Therefore, the required equation of the directrix is y = -1.

问题 20. 写出焦点 (0, 0) 和准线 x + y − 4 = 0 的抛物线方程。

解决方案：

Given that the focus (0, 0) and directrix x + y − 4 = 0 of the parabola

Now, let us assume P (x, y) be any point on the parabola with the given focus and directrix

So, first we draw PM perpendicular to x + y = 4.

Then, 

SP = PM

SP² = PM²

(x – 0)² + (y – 0)² = 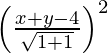$\left( \frac{x + y - 4}{\sqrt{1 + 1}} \right)^2$

x² + y² = 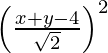$\left( \frac{x + y - 4}{\sqrt{2}} \right)^2$

2x² + 2y² = x² + y² + 16 + 2xy – 8y – 8x

=> x² + y² – 2xy + 8x + 8y – 16 = 0

Hence, the equation of the parabola is x² + y² – 2xy + 8x + 8y – 16 = 0