第 11 类 RD Sharma 解决方案 - 第 25 章抛物线 - 练习 25.1 |设置 1

问题 1. 求抛物线方程：

(i) 焦点是 (3, 0)，准线是 3x + 4y = 1

解决方案：

Given that focus is (3, 0) and the directrix is 3x + 4y = 1

Let us assume that P (x, y) be any point on the parabola.

So, first we draw PM perpendicular to 3x + 4y = 1.

Then,

SP = PM

SP² = PM²

(x – 3)² + (y – 0)² = 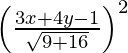$\left( \frac{3x + 4y - 1}{\sqrt{9 + 16}} \right)^2$

(x – 3)² + y² = 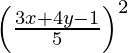$\left( \frac{3x + 4y - 1}{5} \right)^2$

25 (x² + 9 – 6x + y²) = (3x + 4y – 1)²

25x² – 150x + 25y² + 225 = 9x²+ 16y² + 1 + 24xy – 8y – 6x

=> 16x² + 9y² – 24xy – 144x + 8y + 224 = 0

Hence, the equation of the parabola is  16x² + 9y² – 24xy – 144x + 8y + 224 = 0

(ii) 焦点是 (1, 1)，准线是 x + y + 1 = 0

解决方案：

Given that, focus is (1, 1) and the directrix is x + y + 1 = 0

Let us assume P (x, y) be any point on the parabola. 

So, first we draw PM perpendicular to x + y + 1 = 0.

Then, 

SP = PM

SP² = PM²

(x – 1)² + (y – 1)² = $\left| \frac{x + y + 1}{\sqrt{1 + 1}} \right|^2$

(x – 1)² + (y – 1)² = $\left( \frac{x + y + 1}{\sqrt{2}} \right)^2$

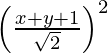
2 (x² + 1 – 2x + y² + 1 – 2y) = x² + y² + 1 + 2xy + 2y + 2x

(2x² + 2 – 4x + 2 y² + 2 – 4y) = x² + y² + 1 + 2xy + 2y + 2x

=> x² + y² – 2xy – 6x – 6y + 3 = 0

Hence, the equation of the parabola is x² + y² – 2xy – 6x – 6y + 3 = 0

(iii) 焦点是 (0, 0)，准线 2x - y - 1 = 0

解决方案：

Given that focus is (0, 0) and the directrix 2x − y − 1 = 0

Let us assume P (x, y) be any point on the parabola. 

So, the first we draw PM perpendicular to 2x − y − 1 = 0.

Then, 

SP = PM

SP² = PM²

(x – 0)² + (y – 0)² = 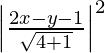$\left| \frac{2x - y - 1}{\sqrt{4 + 1}} \right|^2$

x² + y² = 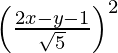$\left( \frac{2x - y - 1}{\sqrt{5}} \right)^2$

5x² + 5 y² = 4x² + y² + 1 – 4xy + 2y – 4x

=> x² + 4y² + 4xy – 2y + 4x – 1 = 0

Hence, the equation of the parabola is x² + 4y² + 4xy – 2y + 4x – 1 = 0

(iv) 焦点是 (2, 3)，准线 x - 4y + 3 = 0。

解决方案：

Given that focus is (2, 3) and the directrix x − 4y + 3 = 0

Let us assume P (x, y) be any point on the parabola. 

So, the first we draw PM perpendicular to x − 4y + 3 = 0.

Then, 

SP = PM

SP² = PM²

(x – 2)² + (y – 3)² = $\left| \frac{x - 4y + 3}{\sqrt{1 + 16}} \right|^2$

(x – 2)² + (y – 3)² = $\left( \frac{x - 4y + 3}{\sqrt{17}} \right)^2$

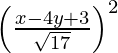
17 (x² + 4 – 4x + y² – 6y + 9) = x² + 16y² + 9 – 8xy – 24y + 6x

17x² – 68x – 102y + 17y² + 13 (17) = x² + 16y² + 9 – 8xy – 24y + 6x

=> 16x² + y² + 8xy – 74x – 78y + 212 = 0

Hence, the equation of the parabola is 16x² + y² + 8xy – 74x – 78y + 212 = 0

问题 2. 求抛物线方程，其焦点是点 (2, 3)，准线是直线 x − 4y + 3 = 0。另外，求它的直角长度。

解决方案：

Given that, focus is (2, 3) and directrix is the line x − 4y + 3 = 0.

Let us assume P (x, y) be any point on the parabola. 

So, first we draw PM perpendicular to x − 4y + 3 = 0.

Then,

SP = PM

SP² = PM²

(x – 2)² + (y – 3)² = 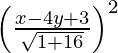$\left( \frac{x - 4y + 3}{\sqrt{1 + 16}} \right)^2$

(x – 2)² + (y – 3)² = $\left( \frac{x - 4y + 3}{\sqrt{17}} \right)^2$

17 (x² + 4 – 4x + y² – 6y + 9) = x² + 16y² + 9 – 8xy – 24y + 6x

17x² – 68x + 17y² – 102y + 9 (17) = x² + 16y² + 9 – 8xy – 24y + 6x

16x² + y² + 8xy – 74x – 78y + 212 = 0

Length of the latus rectum = 2 (Length of the perpendicular from the focus on the directrix)

= $2\left| \frac{2 - 12 + 3}{\sqrt{16 + 1}} \right|$

= $2\left| \frac{- 7}{\sqrt{17}} \right|$

= $2\left( \frac{7}{\sqrt{17}} \right)$

= 4/√17

Hence, the the length of its latus-rectum is 4/√17

问题 3. 求抛物线方程 if

(i) 焦点在 (-6, -6)，顶点在 (-2, 2)

解决方案：

Give that, the focus is at (−6, −6) and the vertex is at (−2, 2)

Let us assume (x₁, y₁) be the coordinates of the point of intersection of the axis and directrix.

So, the slope of the axis of the parabola = $\frac{- 6 - 2}{- 6 + 2}$ = -8/-4 = 2

And the slope of the directrix = -1/2

Let us assume the directrix intersects the axis at point K (r, s), so

(r – 6)/2 = -2, (s – 6)/2 = 2

=> r = 2, s = 10

The equation of the directrix is,

y – 10 = -1/2 (x – 2)

=> 2y + x – 22 = 0

Now, let us assume P (x, y) be any point on the parabola

focus is S (−6, −6). 

And the directrix is 2y + x – 22 = 0.

So, first we draw PM perpendicular to 2x + y + 22 = 0.

Then, 

SP = PM

SP² = PM²

(x + 6)² + (y + 6)² = 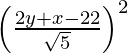$\left( \frac{2y + x - 22}{\sqrt{5}} \right)^2$

5 (x² + 12x + 36 + y² + 12y + 36) = 4y² + x² + 484 + 4xy – 88y – 44x

4x² + y² – 4xy + 104x + 148y – 124 = 0

=> (2x – y)² – 4 (26x + 37y – 31) = 0

Hence, the equation of the parabola is (2x – y)² – 4 (26x + 37y – 31) = 0

(ii) 焦点在 (0, -3)，顶点在 (0, 0)

解决方案：

Given that the focus is at (0, −3) and the vertex is at (0, 0) 

Let us assume (x₁, y₁) be the coordinates of the point of intersection of the axis and directrix.

Thus, the slope of the axis of the parabola cannot be defined.

So, the slope of the directrix = 0

Let us assume the directrix intersect the axis at K (r, s).

(r + 0)/2 = 0, (s – 3)/2 = 0

=> r = 0, s = 3

So, the equation of directrix is y = 3

Let us assume P (x, y) be any point on the parabola 

With focus is S (0, −3) and the directrix is y = 3.

So, first we draw PM perpendicular to y = 3.

Then, 

SP = PM

SP² = PM²

(x – 0)² + (y + 3)² = 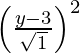$\left( \frac{y - 3}{\sqrt{1}} \right)^2$

x² + y² + 6y + 9 = y² – 6y + 9

=> x² = -12y

Hence, the equation of the parabola is x² = -12y

(iii) 焦点在 (0, -3)，顶点在 (-1, -3)

解决方案：

Given that, focus is at (0, −3) and the vertex is at (−1, −3)

Let us assume (x₁, y₁) be the coordinates of the point of intersection of the axis and directrix.

So, the slope of the axis of the parabola is zero and, the slope of the directrix is 

(r + 0)/2 = -1, (s – 3)/2 = – 3

=> r = – 2, s = – 3

The equation of the directrix is x + 2 = 0.

Let us assume P (x, y) be any point on the parabola whose focus is S (0, −3) and the directrix is x + 2 = 0.

So, first we draw PM perpendicular to x + 2 = 0

Then, 

SP = PM

SP² = PM²

(x – 0)² + (y + 3)² = 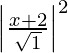$\left| \frac{x + 2}{\sqrt{1}} \right|^2$

x² + y² + 6y + 9 = x² + 4x + 4

=> y² + 6y – 4x + 5 = 0

Hence, the equation of the parabola is y² + 6y – 4x + 5 = 0

(iv) 焦点在 (a, 0)，顶点在 (a', 0)

解决方案：

Given that focus is at (a, 0) and the vertex is at (a’, 0) 

Let us assume (x₁, y₁) be the coordinates of the point of intersection of the axis and directrix.

So, the slope of the axis of the parabola is zero and, the slope of the directrix cannot be defined.

Let us assume the directrix intersect the axis at point K (r, s).  

So, (r + a)/2 = a’, (s + 0)/2 = 0

=> r = 2a’ – a, s = 0

The equation of the directrix is x – 2a’ + a = 0  

Let us assume P (x, y) be any point on the parabola 

with focus is S (a, 0), and the directrix is x – 2a’ + a = 0. 

So, first we draw PM perpendicular to x – 2a’ + a = 0  

Then,

SP = PM

SP² = PM²

(x – a)² + (y – 0)² = 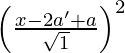$\left( \frac{x - 2a' + a}{\sqrt{1}} \right)^2$

y² = (x – 2a’ + a)² – (x – a)²

y² = x² + 4a’² + a² – 4a’x – 4aa’ + 2ax – x² – a² + 2ax

y² = 4a’² – 4a’x – 4aa’ + 4ax

=> y² = -4 (a’ – a) (x – a’)

Hence, the equation of the parabola is y² = -4 (a’ – a) (x – a’)

(v) 焦点位于 (0, 0)，顶点位于线 x + y = 1 和 x - y = 3 的交点处。

解决方案：

Given that focus is at (0, 0) and vertex is at the intersection of the lines x + y = 1 and x − y = 3. 

Let us assume (x₁, y₁) be the coordinates of the point of intersection of the axis and directrix.

So, the slope of the axis of the parabola = $\frac{- 6 - 2}{- 6 + 2}$ = -8/-4 = 2

And the slope of the directrix = -1/2

Let us assume the directrix intersect the axis at point K (r, s).  

so, (r – 6)/2 = -2, (s – 6)/2 = 2

=> r = 2, s = 10

The equation of the directrix is,

y – 10 = -1/2 (x – 2)

=> 2y + x – 22 = 0

Now, let us assume P (x, y) be any point on the parabola

With focus is S (−6, −6) and the directrix is 2y + x – 22 = 0.

So, first we draw PM perpendicular to 2x + y + 22 = 0.

Then, 

SP = PM

SP² = PM²

(x + 6)² + (y + 6)² = 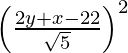$\left( \frac{2y + x - 22}{\sqrt{5}} \right)^2$

5 (x² + 12x + 36 + y² + 12y + 36) = 4y² + x² + 484 + 4xy – 88y – 44x

4x² + y² – 4xy + 104x + 148y – 124 = 0

=> (2x – y)² – 4 (26x + 37y – 31) = 0

Hence, the equation of the parabola is (2x – y)² – 4 (26x + 37y – 31) = 0

问题 4. 求下列抛物线的顶点、焦点、轴、准线和直角：

(i) y ² = 8x

解决方案：

Given that, y² = 8x  

Now, on comparing the given equation with y² = 4ax, we get

=> 4a = 8 

=> a = 2

So, the vertex = (0, 0)

Focus = (a, 0) = (2, 0)

The equation of the directrix is 

x = −a

=> x = −2

Axis = y = 0

Length of the latus rectum = 4a = 4(2) = 8 units

(ii) 4x ² + y = 0

解决方案：

Given that, 

 4x² + y = 0  

=> -y/4 = x²  

Now, on comparing the given equation with x² = -4ay, we get

=> 4a = 1/4 

=> a = 1/16

So, the vertex = (0, 0)

Focus = (0, −a) = (0, -1/16)

Equation of the directrix, y = a

=> y = 1/16

Axis = x = 0

Length of the latus rectum = 4a = 4 (1/16) = 1/4 units

(iii) y ² - 4y - 3x + 1 = 0

解决方案：

Given that, 

y² − 4y − 3x + 1 = 0  

(y – 2)² – 4 – 3x + 1 = 0

(y – 2)² = 3 (x + 1)

(y – 2)² = 3 (x – (-1))

Let us assume Y = y – 2 and X = x + 1.

Then, 

Y² = 3X

Now, on comparing the given equation with Y² = 4aX, we get

=> 4a = 3 

=> a = 3/4

So, the vertex = (X = 0, Y = 0) = (x = -1, y = 2)

Focus = (X = a, Y = 0) = (x + 1 = 3/4, y – 2 = 0) = (x = -1/4, y = 2)

Equation of the directrix: X = −a

i.e. x + 1 = -3/4 

=> x = -7/4

Axis = Y = 0

i.e. y – 2 = 0 

=> y = 2

Length of the latus rectum = 4a = 4 (3/4) = 3 units

(iv) y ² - 4y + 4x = 0

解决方案：

Given that, 

y² − 4y + 4x = 0  

(y – 2)² – 4 + 4x = 0

(y – 2)² = -4 (x – 1)

Let us assume Y = y – 2 and X = x – 1.

Then, 

=> Y² = – 4X

Now, on comparing the given equation with Y² = -4aX, we get

=> 4a = 4 

=> a = 1

So, the vertex = (X = 0, Y = 0) = (x = 1, y = 2)

Focus = (X = −a, Y = 0) = (x – 1 = – 1, y – 2 = 0) = (x = 0, y = 2)

Equation of the directrix: X = a  

i.e. x – 1 = 1 

=> x = 2

Axis = Y = 0

i.e. y – 2 = 0 

=> y = 2

Length of the latus rectum = 4a = 4 (1) = 4 units

(v) y ² + 4x + 4y - 3 = 0

解决方案：

Given that

y² + 4y + 4x −3 = 0  

(y + 2)² – 4 + 4x – 3 = 0

(y + 2)² = – 4 (x – 7/4)

Let us assume Y = y + 2 and X = x – 7/4

Then, Y² = – 4X.

Now, on comparing the given equation with Y² = -4aX 

=> 4a = 4 

=> a = 1

So, the Vertex = (X = 0, Y = 0) = (x = 7/4, y = – 2)

Focus = (X = −a, Y = 0) = (x – 7/4 = – 1, y + 2 = 0) = (x = 3/4, y = – 2)

Equation of the directrix: X = a

i.e. x – 7/4 = 1 

=> x = 11/4

Axis = Y = 0

i.e. y + 2 = 0 

=> y = – 2

Length of the latus rectum = 4a = 4 (1) = 4 units

(vi) y ² = 8x + 8y

解决方案：

Given that

y² = 8x + 8y  

(y – 4)² = 8 (x + 2)

On putting Y = y – 4 and X = x + 2, we get

Y² = 8X

On comparing the given equation with Y² = 4aX, we get

=> 4a = 8 

=> a = 2

So, the vertex = (X = 0, Y = 0) = (x = – 2, y = 4)

Focus = (X = a, Y = 0) = (x + 2 = 2, y – 4 = 0) = (x = 0, y = 4)

Equation of the directrix: X = −a  

i.e. x + 2 = – 2 

=> x + 4 = 0

Axis = Y = 0

i.e. y –  4 = 0 

=> y = 4

Length of the latus rectum = 4a = 4 (2) = 8 units

(vii) 4 (y - 1) ² = - 7 (x - 3)

解决方案：

Given that

4(y − 1)² = − 7 (x − 3)  

(y – 1)² = -7/4 (x – 3)

Let Y = y – 1 and X = x – 3.

Then, 

Y² = -7/4 X  

On comparing the given equation with Y² = – 4aX, we get

=> 4a = 7/4

=> a = 7/16

So, the vertex = (X = 0, Y = 0) = (x = 3, y = 1)  

Focus = (X = −a, Y = 0) = (x – 3 = -7/16, y – 1 = 0) = (x = 41/16, y = 1)

Equation of the directrix: X = a

i.e. x – 3 = 7/16 

=> x = 55/16

Axis = Y = 0

i.e. y – 1 = 0 

=> y = 1  

Length of the latus rectum = 4a = 4 (7/16) = 7/4 units

(viii) y ² = 5x - 4y - 9

解决方案：

Given that,

y² = 5x − 4y − 9  

y² + 4y = 5x – 9

(y + 2)² = 5x – 5 

(y + 2)² = 5 (x – 1)

On putting Y = y + 2 and X = x – 1, we get

Y² = 5X

On comparing the given equation with Y² = 4aX, we get

=> 4a = 5 

=> a = 5/4

So the vertex = (X = 0, Y = 0) = (x = 1, y = -2)

Focus = (X = a, Y = 0) = (x – 1 = 5/4, y + 2 =0) = (x = 9/4, y = -2)

Equation of the directrix: X = −a

i.e. x – 1 = -5/4 

=> x = -1/4

Axis = Y = 0

i.e. y + 2 = 0 

=> y = – 2

Length of the latus rectum = 4a = 4 (5/4) = 5 units

(ix) x ² + y = 6x - 14

解决方案：

Given that

x² = 6x − y − 14  

(x – 3)² = -y – 14 + 9

(x – 3)² = -y – 5 

(x – 3)² = – (y + 5)

Let us assume Y = y + 5 and X = x – 3.

Then, 

X² = – Y

On comparing the given equation with X² = – 4aY, we get

=> 4a = 1 

=> a = 1/4

So, the vertex = (X = 0, Y = 0) = (x = 3, y = – 5)

Focus = (X = 0, Y = −a) = (x – 3 = 0, y + 5 = -1/4) = (x = 3, y = -21/4)

Equation of the directrix: Y = a

i.e. y + 5 = 1/4 

=> y = -19/4

Axis = X = 0

i.e.  x – 3 = 0 

=> x = 3

Length of the latus rectum = 4a = 4 (1/4) = 1 units

问题 5. 对于抛物线，y ² = 4px 找到长度为 8p 的双纵坐标的末端。证明从顶点到端点的线成直角。

解决方案：

Given that the equation of the parabola is y² = 4px.

Let us assume PQ be the double coordinate of length 8p of the parabola and let A be the vertex of parabola.

y² = 4px

Then, 

PR = RQ = 4p  

Let AR = x₁

So, the coordinates of P and Q are (x₁ , 4p) and (x₁, -4p)

Now, P lies on y² = 4px.

So, (4p)² = 4p x₁  

=> x₁ = 4p

So, the coordinates of P is (4p, 4p) and Q is (4p, -4p)

The coordinates of A are (0, 0).  

So, m₁ = Slope of AP = $\frac{4p - 0}{4p - 0}$ = 4p/4p = 1

And, m₂ = Slope of AQ = $\frac{\left( - 4p - 0 \right)}{4p - 0}$ = -4p/4p =  -1

Now,  

m₁ m₂ = – 1

Thus, AP is perpendicular to AQ.

Hence proved.

问题 6. 求抛物线的顶点 x ² = 12y 到直角直角末端的连线形成的三角形面积。

解决方案：

Given that the equation of the parabola is x² = 12y.

Now on comparing the given equation with x² = 4ay, we get

=> 4a = 12

=> a = 3  

So, the coordinates of focus are (0, 3).

Now two points lie on the parabola.

=> x² = 12 (3)

=> x² = 36

=> x = ±6

Therefore, the points are P (6, 3) and Q (-6, 3).

Distance PQ = $\sqrt{(6 - (-6))^2 + (3 - 3)^2}$

= $\sqrt{(6 + 6)^2 + (3 - 3)^2}$

= $\sqrt{(12)^2 + (0)^2}$

= 12

Area = (PQ) (3) (1/2)

= (12) (3) (1/2)

= 18 sq. units

Therefore, the area of the triangle formed by the lines joining the vertex of the given parabola to the ends of its latus rectum is 18 sq. units.

问题 7. 求焦点为 (3, 3) 且准线为 3x − 4y = 2 的抛物线的轴与准线的交点坐标。求直肠宽的长度。

解决方案：

Given that the equation of the directrix is 3x − 4y = 2.  

So, the slope of the directrix = -3/-4 = 3/4

Axis is perpendicular to the directrix.

so, the lope of the axis = -4/3

Now, the focus lies on the axis of the parabola.

So, the equation of the axis is 

=> y – 3 = (-4/3) (x – 3)

=> 3y – 9 = -4x + 12

=> 3y + 4x – 21 = 0

On solving equations (1) and (2), we get

x = 18/5, y = 11/5

So, the intersection point of the axis and directrix is (18/5, 11/5).

Ad the length of the latus rectum = 2 (Length of the perpendicular from the focus on the directrix)  

= $2\left| \frac{3\left( 3 \right) + \left( - 4 \right)3 - 2}{\sqrt{16 + 9}} \right|$

= $2\left| \frac{- 5}{\sqrt{16 + 9}} \right|$

= 2

问题 8. 在抛物线 x ² = 9y 的哪一点上，横坐标是坐标的三倍？

解决方案：

We have,

=> x² = 9y

Now by putting x = 3y in the given equation of the parabola, we get

=> 9y² = 9y

=> 9y (y – 1) = 0

=> y = 0, 1

At y = 0, x = 0.

And also at y = 1, x = 3.

Therefore, at (1, 3), the abscissa is three times that of the coordinate.

问题 9. 求以顶点为原点，轴沿 x 轴，通过 (2, 3) 的抛物线方程。

解决方案：

Let us consider the equation of the required parabola be,

=> y² = 4ax

Since it passes through (2, 3), we get,

=> 9 = 4a (2)

=> 8a = 9

=> a = 9/8

So, the equation is y² = $\frac{4\left( 9 \right)x}{8}$

i.e. 2y² = 9x

Let us assume the equation of the required parabola be y² = -4ax.

Since the above equation passes through (2, 3), we get

=> 9 = – 4a (2) 

=> 8a = -9

=> a = -9/8

Hence, the equation is, 

=> y² = $\frac{- 4\left( - 9 \right)x}{8}$

=> 2y² = 9x  

Hence, in either case, the required equation of the parabola is 2y² = 9x.

问题 10. 求以顶点为原点和准线 y = 2 的抛物线方程。

解决方案：

Given that, vertex is (0, 2) and the directrix is y = 2. 

Let us assume (x₁, y₁) be the coordinates of the point of intersection of the axis and directrix.

=> (x₁, y₁) = (0, 2)

Let us assume the focus be (x₂, y₂).

Now, 

(x₂ + 0)/2 = 0 and (y₂ + 2)/2 = 0

=> x₂ = 0 and y₂ = -2

The coordinates of focus are (0, -2).

First we draw PM perpendicular to y = 2.

Then, we have:

SP = PM

SP² = PM²

(x – 0)² + (y + 2)² = 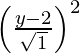$\left(\frac{y-2}{\sqrt{1}} \right)^2$

(x – 0)² + (y + 2)² = (y – 2)²

x² + y² + 4 + 4y = y² + 4 – 4y

x² = -4y – 4y

=> x² = -8y

Hence, the equation of parabola is x² = -8y.