向量和信号之间的类比

向量和信号之间有一个完美的类比。

向量

向量包含大小和方向。矢量的名称用粗体字表示，其大小用浅色字型表示。

示例： V是一个幅值为V的向量。考虑两个向量V ₁和V ₂ ，如下图所示。令V ₁与V ₂的分量由C ₁₂ V _2给出。向量V ₁与向量V ₂的分量可以通过从V ₁的末端到向量V ₂的垂直线获取，如图所示：

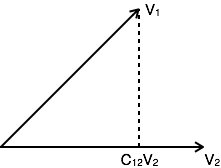
向量V ₁可以用向量V _2表示

V ₁ = C ₁₂ V ₂ + V _e

其中Ve是误差向量。

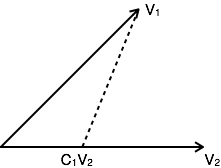
但这不是用V ₂表示向量V ₁的唯一方法。替代的可能性是：

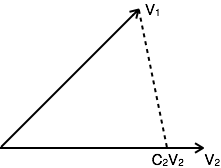
对于大元件值，误差信号最小。如果C ₁₂ = 0，则两个信号被称为正交。

两个向量的点积

V ₁ 。 V ₂ = V _{1·V 2COSθ}

θ= V1和V2之间的角度

V ₁ 。 V ₂ = V ₂ .V ₁

V ₁ alog _n V ₂的分量V ₂ = V ₁ Cosθ= $ V1.V2 \超过V2 $

从图中可以看出，V ₁ alog _n V ₂ = C ₁₂ V _2的分量

$$ V_1.V_2 \超过V_2 = C_12 \，V_2 $$

$$ \ Rightarrow C_ {12} = {V_1.V_2 \超过V_2} $$

信号

正交性的概念可以应用于信号。让我们考虑两个信号f ₁ (t)和f ₂ (t)。与向量类似，您可以根据f ₂ (t)将f ₁ (t)近似为

对于(t ₁ 2 )，f ₁ (t)= C ₁₂ f ₂ (t)+ f _e (t)

$ \ Rightarrow $ f _e (t)= f ₁ (t)– C ₁₂ f ₂ (t)

最小化误差的一种可能方式是在t ₁至t ₂的间隔内积分。

$$ {1 \ over {t_2-t_1}} \ int_ {t_1} ^ {t_2} [f_e(t)] dt $$

$$ {1 \ over {t_2-t_1}} \ int_ {t_1} ^ {t_2} [f_1(t)-C_ {12} f_2(t)] dt $$

但是，此步骤也不会将错误降低到可观的程度。这可以通过采用误差平方函数来纠正。

$ \ varepsilon = {1 \ over {t_2-t_1}} \ int_ {t_1} ^ {t_2} [f_e(t)] ^ 2 dt $

$ \ Rightarrow {1 \ over {t_2-t_1}} \ int_ {t_1} ^ {t_2} [f_e(t)-C_ {12} f_2] ^ 2 dt $

其中ε是误差信号的均方值。将误差最小化的C ₁₂值，您需要计算$ {d \ varepsilon \ over dC_ {12}} = 0 $

$ \ Rightarrow {d \ over dC_ {12}} [{1 \ over t_2-t_1} \ int_ {t_1} ^ {t_2} [f_1(t)-C_ {12} f_2(t)] ^ 2 dt] = 0 $

$ \ Rightarrow {1 \ over {t_2-t_1}} \ int_ {t_1} ^ {t_2} [{d \ over dC_ {12}} f_ {1} ^ 2(t)-{d \ over dC_ {12} } 2f_1(t)C_ {12} f_2(t)+ {d \ over dC_ {12}} f_ {2} ^ {2}(t)C_ {12} ^ 2] dt = 0 $

没有C12项的项的导数为零。

$ \ Rightarrow \ int_ {t_1} ^ {t_2}-2f_1(t)f_2(t)dt + 2C_ {12} \ int_ {t_1} ^ {t_2} [f_ {2} ^ {2}(t)] dt = 0 $

如果$ C_ {12} = {{\ int_ {t_1} ^ {t_2} f_1(t)f_2(t)dt} \ over {\ int_ {t_1} ^ {t_2} f_ {2} ^ {2}(t )dt}} $分量为零，则称两个信号正交。

将C ₁₂ = 0以获得正交条件。

0 = $ {{\ int_ {t_1} ^ {t_2} f_1(t)f_2(t)dt} \ over {\ int_ {t_1} ^ {t_2} f_ {2} ^ {2}(t)dt}} $

$$ \ int_ {t_1} ^ {t_2} f_1(t)f_2(t)dt = 0 $$

正交向量空间

正交向量的完整集合称为正交向量空间。考虑如下所示的三维向量空间：

考虑在点(X ₁ ，Y ₁ ，Z ₁ )上的向量A。考虑分别沿X，Y，Z轴方向的三个单位矢量(V _X ，V _Y ，V _Z )。由于这些单位向量是相互正交的，因此满足

$$ V_X。 V_X = V_Y。 V_Y = V_Z。 V_Z = 1 $$

$$ V_X。 V_Y = V_Y。 V_Z = V_Z。 V_X = 0 $$

您可以将以上条件写为

$$ V_a。 V_b = \ left \ {\ begin {array} {ll} 1＆\ quad a = b \\ 0＆\ quad a \ neq b \ end {array} \ right。 $$

向量A可以用其分量和单位向量表示为

$ A = X_1 V_X + Y_1 V_Y + Z_1 V_Z …….(1)$

该三维空间中的任何矢量都只能用这三个单位矢量来表示。

如果考虑n维空间，则该空间中的任何向量A都可以表示为

$ A = X_1 V_X + Y_1 V_Y + Z_1 V_Z + … + N_1V_N …..(2)$

由于单位矢量的大小对于任何矢量A都是统一的

沿x轴的A分量= AV _X

A沿Y轴的分量= AV _Y

A沿Z轴的分量= AV _Z

同样，对于n维空间，A沿某些G轴的分量

$ = A.VG ……(3)$

将方程式2代入方程式3。

$ \ Rightarrow CG =(X_1 V_X + Y_1 V_Y + Z_1 V_Z + … + G_1 V_G … + N_1V_N)V_G $

$ = X_1 V_X V_G + Y_1 V_Y V_G + Z_1 V_Z V_G + … + G_1V_G V_G … + N_1V_N V_G $

$ = G_1 \，\，\，\，\，\ text {因为} V_G V_G = 1 $

$如果V_G V_G \ neq 1 \，\，\ text {ie} V_G V_G = k $

$ AV_G = G_1V_G V_G = G_1K $

$ G_1 = {(AV_G)\ over K} $

正交信号空间

让我们考虑在t ₁至t ₂的间隔内的n个相互正交的函数x ₁ (t)，x ₂ (t)… x _n (t)的集合。由于这些函数彼此正交，所以任何两个信号x _j (t)，x _k (t)必须满足正交性条件。即

$$ \ int_ {t_1} ^ {t_2} x_j(t)x_k(t)dt = 0 \，\，\，\ text {where} \，j \ neq k $$

$$ \ text {Let} \ int_ {t_1} ^ {t_2} x_ {k} ^ {2}(t)dt = k_k $$

设函数f(t)，可以通过沿相互正交的信号相加分量，用该正交信号空间近似

$ \，\，\，f(t)= C_1x_1(t)+ C_2x_2(t)+ … + C_nx_n(t)+ f_e(t)$

$ \ quad \ quad = \ Sigma_ {r = 1} ^ {n} C_rx_r(t)$

$ \，\，\，f(t)= f(t)-\ Sigma_ {r = 1} ^ n C_rx_r(t)$

平均平方误差$ \ varepsilon = {1 \ t_2-t_2} \ int_ {t_1} ^ {t_2} [f_e(t)] ^ 2 dt $

$$ = {1 \ over t_2-t_2} \ int_ {t_1} ^ {t_2} [f [t]-\ sum_ {r = 1} ^ {n} C_rx_r(t)] ^ 2 dt $$

可以找到使均方误差最小的分量

$$ {d \ varepsilon \ over dC_1} = {d \ varepsilon \ over dC_2} = … = {d \ varepsilon \ over dC_k} = 0 $$

让我们考虑$ {d \ varepsilon \ over dC_k} = 0 $

$$ {d \ over dC_k} [{1 \ over t_2-t_1} \ int_ {t_1} ^ {t_2} [f(t)-\ Sigma_ {r = 1} ^ n C_rx_r(t)] ^ 2 dt] = 0 $$

所有不包含C _k的项均为零。即，总而言之，r = k项保留，所有其他项为零。

$$ \ int_ {t_1} ^ {t_2}-2 f(t)x_k(t)dt + 2C_k \ int_ {t_1} ^ {t_2} [x_k ^ 2(t)] dt = 0 $$

$$ \ Rightarrow C_k = {{\ int_ {t_1} ^ {t_2} f(t)x_k(t)dt} \ over {int_ {t_1} ^ {t_2} x_k ^ 2(t)dt}} $$

$$ \ Rightarrow \ int_ {t_1} ^ {t_2} f(t)x_k(t)dt = C_kK_k $$

均方误差

误差函数f _e (t)的平方的平均值称为均方误差。用ε(ε)表示。

。

$ \ varepsilon = {1 \ t_2-t_1} \ int_ {t_1} ^ {t_2} [f_e(t)] ^ 2dt $

$ \，\，\，\，== {1 \ t t_2-t_1} \ int_ {t_1} ^ {t_2} [f_e(t)-\ Sigma_ {r = 1} ^ n C_rx_r(t)] ^ 2 dt $

$ \，\，\，\，= {1 \ t t_2-t_1} [\ int_ {t_1} ^ {t_2} [f_e ^ 2(t)] dt + \ Sigma_ {r = 1} ^ {n} C_r ^ 2 \ int_ {t_1} ^ {t_2} x_r ^ 2(t)dt-2 \ Sigma_ {r = 1} ^ {n} C_r \ int_ {t_1} ^ {t_2} x_r(t)f(t)dt $

您知道$ C_ {r} ^ {2} \ int_ {t_1} ^ {t_2} x_r ^ 2(t)dt = C_r \ int_ {t_1} ^ {t_2} x_r(t)f(d)dt = C_r ^ 2 K_r $

$ \ varepsilon = {1 \ t_2-t_1} [\ int_ {t_1} ^ {t_2} [f ^ 2(t)] dt + \ Sigma_ {r = 1} ^ {n} C_r ^ 2 K_r-2 \ Sigma_ {r = 1} ^ {n} C_r ^ 2 K_r] $

$ \，\，\，\，= {1 \ t_2-t_1} [\ int_ {t_1} ^ {t_2} [f ^ 2(t)] dt-\ Sigma_ {r = 1} ^ {n} C_r ^ 2 K_r] $

$ \，\因此\ varepsilon = {1 \ t_2-t_1} [\ int_ {t_1} ^ {t_2} [f ^ 2(t)] dt +(C_1 ^ 2 K_1 + C_2 ^ 2 K_2 + … + C_n ^ 2 K_n)] $

上式用于评估均方误差。

封闭和完整的正交函数集

让我们考虑在t ₁至t ₂的间隔内的一组n个相互正交的函数x ₁ (t)，x ₂ (t)… x _n (t)。当不存在满足条件$ \ int_ {t_1} ^ {t_2} f(t)x_k(t)dt = 0 $的函数f(t)时，这称为封闭完整集。

如果此函数满足公式$ \ int_ {t_1} ^ {t_2} f(t)x_k(t)dt = 0 \，\，\ text {for} \，k = 1,2，.. $，则f (t)被认为与正交集的每个函数正交。没有f(t)，该集合是不完整的。当包含f(t)时，它将变为闭合并完成设置。

通过沿相互正交的信号相加分量，可以用该正交集来近似f(t)

$$ f(t)= C_1 x_1(t)+ C_2 x_2(t)+ … + C_n x_n(t)+ f_e(t)$$

如果无穷级数$ C_1 x_1(t)+ C_2 x_2(t)+ … + C_n x_n(t)$收敛到f(t)，则均方误差为零。

复函数中的正交性

如果f ₁ (t)和f ₂ (t)是两个复数函数，则f ₁ (t)可以用f ₂ (t)表示为

$ f_1(t)= C_ {12} f_2(t)\，\，\，\，\，\，\，\，$ ..，误差可忽略不计

其中$ C_ {12} = {{\ int_ {t_1} ^ {t_2} f_1(t)f_2 ^ *(t)dt} \ over {\ int_ {t_1} ^ {t_2} | f_2(t)| ^ 2 dt}} $

其中$ f_2 ^ *(t)$ = f ₂ (t)的复共轭。

如果f ₁ (t)和f ₂ (t)正交，则C ₁₂ = 0

$$ {\ int_ {t_1} ^ {t_2} f_1(t)f_2 ^ *(t)dt \ over \ int_ {t_1} ^ {t_2} | f_2(t)| ^ 2 dt} = 0 $$

$$ \ Rightarrow \ int_ {t_1} ^ {t_2} f_1(t)f_2 ^ *(dt)= 0 $$

上式表示复函数中的正交性条件。