光的衍射
干涉、折射、反射和衍射都是光在空气中传播时发生的过程的例子。光与障碍物接触时会发生衍射。当光流过一个大小与光的波长相当的小开口时,光圈另一侧的波前模拟波。
当光通过宽度(w)在光的波长数量级的单缝时,我们可以看到单缝衍射。屏幕的衍射图案将在距离狭缝 L >> w 处。强度与角度成正比。
什么是衍射?
The bending of light around corners such that it spreads out and illuminates regions, where a shadow is expected, is known as diffraction.
一般来说,很难区分衍射和干涉,因为它们都是同时发生的。光的衍射是我们在天空中看到的银线的原因。当阳光穿过或撞击云层时,天空中会出现一条银线。
当 Young 的双缝实验用一个窄缝代替时,就会出现一个中央有明亮区域的宽图案。中心两侧有交替的暗区和亮区。当您远离中心时,强度会降低。本文深入讨论了光的单缝衍射。
单缝衍射
我们可能会在单缝衍射实验中看到光的弯曲现象或衍射,这会导致来自相干光源的光与自身发生干涉,并在屏幕上形成称为衍射图案的独特图案。当光源小到足以与光的波长相媲美时,就会发生衍射。这种影响可以在下图中看到。大孔径的扩散很小,几乎无法察觉。
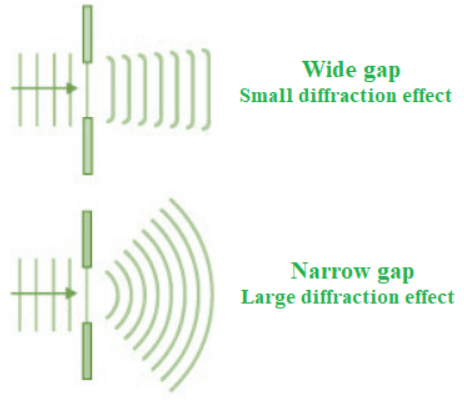
单缝衍射
Formula for Single Slit Diffraction
We’ll denote the slit width a << D, and the distance between the slit and the screen is D.
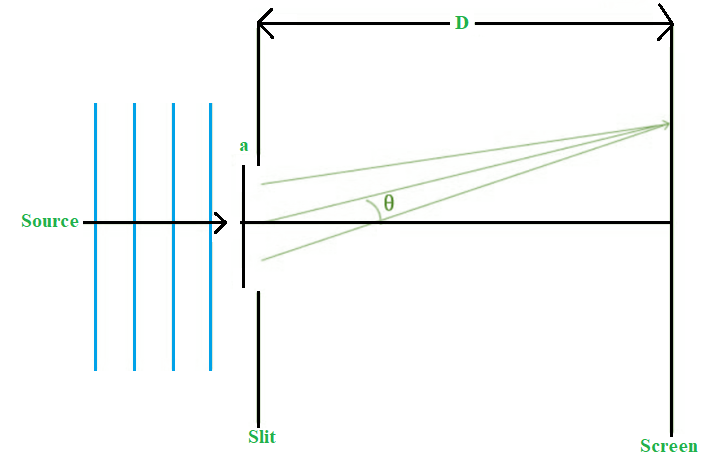
The angular location of any point on the screen will be determined by measuring from the slit centre, which splits the slit by a ⁄ 2 lengths. To explain the pattern, we’ll look at the state of black fringes first. Let us also split the slit into equal-width zones a ⁄ 2. Let’s take a look at a pair of rays that come from a ⁄ 2 distances apart, as illustrated below.

The top two rays indicate the following route difference:
Δ L = (a ⁄ 2) sinθ
Note: Remember that this is only a viable computation if D is really large.
Any number of ray pairs that start at a distance of a ⁄ 2 from one another, such as the bottom two rays in the diagram, can be considered. Any arbitrary pair of rays separated by a ⁄ 2 can be taken into account. In a minute, we’ll discover how important this method is. The path difference must create destructive interference for a dark fringe; the path difference must be out of phase by λ ⁄ 2. (λ represents the wavelength)
For the first fringe,
Δ L = λ ⁄ 2 = a ⁄ 2 sinθ
λ = a sinθ
There is another beam at a distance of a ⁄ 2 that can create destructive interference for a ray coming from any point in the slit. As each ray originating from a point has a counterpart that produces destructive interference, there is destructive interference at θ = sin−1(λ ⁄ a). As a result, a dark fringe is created.
We may divide the slit into four equal portions of a ⁄ 4 and use the same rationale for the next fringe. As a result, for the second minima:
λ ⁄ 2 = a ⁄ 4 sinθ
2λ = a sinθ
Similarly, we may divide the slit into 2n parts for the nth fringe and utilise the following condition:
λ ⁄ 2 = a ⁄ 2n sinθ
n λ = a sinθ
中央最大值
最大值位于最小值之间,中心最大值的宽度等于屏幕两侧一阶最小值之间的距离。
由 y 确定的最小值的位置(从屏幕中心测量)是:
tanθ ≈ θ ≈ y ⁄ D
对于小 θ,
sinθ ≈ θ
⇒ λ = a sinθ ≈ a θ
角宽,
θ = y/D = λa
中央最大值,
y = λ D a
中心最大值的宽度只是这个数量的两倍。
中心最大值的宽度= 2λ D a
中心最大值角宽度= 2θ = 2λ a
示例问题
问题1:阶段之间有什么区别?
回答:
The difference between any two waves or particles with the same frequency and originating from the same place is known as phase difference. It’s measured in radians or degrees.
问题2:相长干涉必须满足什么条件?
回答:
The path difference must be an integral multiple of the wavelength in order for constructive interference to occur.
问题3:产生有害干扰的要求是什么?
回答:
The path difference must equal an odd integral multiple of half-wavelength for destructive interference to occur.
问题 4:什么是时间连贯性,它是什么意思?
回答:
The connection between the field at one place and the field at the same point at a later time is known as temporal coherence.
问题 5:什么是康普顿效应,它是如何工作的?
回答:
When X-rays and gamma rays are dispersed, the Compton effect occurs, which causes the wavelength of the radiation to rise.