绘画围栏算法

给定具有n个杆和k种颜色的围栏，请找出对围栏进行涂漆的方法，以使最多2个相邻的柱具有相同的颜色。由于答案可能很大，因此以10 ^ 9 + 7为模。
例子：

Input : n = 2 k = 4
Output : 16
We have 4 colors and 2 posts.
Ways when both posts have same color : 4 
Ways when both posts have diff color :
4(choices for 1st post) * 3(choices for 
2nd post) = 12

Input : n = 3 k = 2
Output : 6

下图描述了用2种颜色绘制3个帖子的6种可能方法：

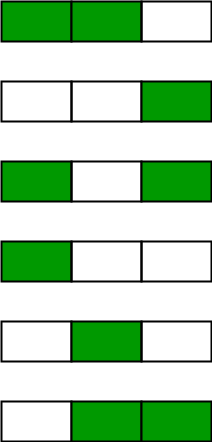
考虑以下图像，其中c，c’和c”分别是桩i，i-1和i -2的颜色。

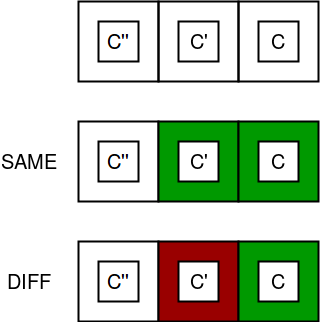
根据问题的约束，c = c’= c”是不可能同时发生的，因此c’！= c或c”！= c或两者兼而有之。 c’！= c有k – 1个可能性，而c”！= c有k – 1个可能性。

diff = no of ways when color of last
        two posts is different
 same = no of ways when color of last 
        two posts is same
 total ways = diff + sum

for n = 1
    diff = k, same = 0
    total = k

for n = 2
    diff = k * (k-1) //k choices for
           first post, k-1 for next
    same = k //k choices for common 
           color of two posts
    total = k +  k * (k-1)

for n = 3
    diff = k * (k-1)* (k-1) 
           //(k-1) choices for the first place 
        // k choices for the second place
        //(k-1) choices for the third place
    same = k * (k-1) * 2
        // 2 is multiplied because consider two color R and B
        // R R B or B R R 
        // B B R or R B B  
           c'' != c, (k-1) choices for it

Hence we deduce that,
total[i] = same[i] + diff[i]
same[i]  = diff[i-1]
diff[i]  = (diff[i-1] + diff[i-2]) * (k-1)
         = total[i-1] * (k-1)

下面是该问题的实现：

C++

// C++ program for Painting Fence Algorithm
// optimised version
 
#include 
using namespace std;
 
// Returns count of ways to color k posts
long countWays(int n, int k)
{
    long dp[n + 1];
    memset(dp, 0, sizeof(dp));
    long long mod = 1000000007;
 
    dp[1] = k;
    dp[2] = k * k;
 
    for (int i = 3; i <= n; i++) {
        dp[i] = ((k - 1) * (dp[i - 1] + dp[i - 2])) % mod;
    }
 
    return dp[n];
}
 
// Driver code
int main()
{
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

Java

// Java program for Painting Fence Algorithm
import java.util.*;
 
class GfG {
 
    // Returns count of ways to color k posts
    // using k colors
    static long countWays(int n, int k)
    {
        // To store results for subproblems
        long dp[] = new long[n + 1];
        Arrays.fill(dp, 0);
        int mod = 1000000007;
 
        // There are k ways to color first post
        dp[1] = k;
 
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        int same = 0, diff = k;
 
        // Fill for 2 posts onwards
        for (int i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
 
            // We always have k-1 choices for next post
            diff = (int)(dp[i - 1] * (k - 1));
            diff = diff % mod;
 
            // Total choices till i.
            dp[i] = (same + diff) % mod;
        }
 
        return dp[n];
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}
 
// This code contributed by Rajput-Ji

Python3

# Python3 program for Painting Fence Algorithm
# optimised version
 
# Returns count of ways to color k posts
def countWays(n, k):
     
    dp = [0] * (n + 1)
    total = k
    mod = 1000000007
     
    dp[1] = k
    dp[2] = k * k   
     
    for i in range(3,n+1):
        dp[i] = ((k - 1) * (dp[i - 1] + dp[i - 2])) % mod
         
    return dp[n]
   
# Driver code
n = 3
k = 2
print(countWays(n, k))
  
# This code is contributed by shubhamsingh10

C#

// C# program for Painting Fence Algorithm
using System;
public class GFG
{
 
  // Returns count of ways to color k posts
  // using k colors
  static long countWays(int n, int k)
  {
 
    // To store results for subproblems
    long[] dp = new long[n + 1];
    Array.Fill(dp, 0);
    int mod = 1000000007;
 
    // There are k ways to color first post
    dp[1] = k;
 
    // There are 0 ways for single post to
    // violate (same color_ and k ways to
    // not violate (different color)
    int same = 0, diff = k;
 
    // Fill for 2 posts onwards
    for (int i = 2; i <= n; i++)
    {
 
      // Current same is same as previous diff
      same = diff;
 
      // We always have k-1 choices for next post
      diff = (int)(dp[i - 1] * (k - 1));
      diff = diff % mod;
 
      // Total choices till i.
      dp[i] = (same + diff) % mod;
    }
 
    return dp[n];
  }
 
  // Driver code
  static public void Main ()
  {
    int n = 3, k = 2;
    Console.WriteLine(countWays(n, k));
  }
}
 
// This code is contributed by avanitrachhadiya2155

输出：

6

空间优化：
我们可以优化上述解决方案，以使用一个变量而不是一个表。
下面是该问题的实现：

C++

// C++ program for Painting Fence Algorithm
#include 
using namespace std;
 
// Returns count of ways to color k posts
// using k colors
long countWays(int n, int k)
{
    // There are k ways to color first post
    long total = k;
    int mod = 1000000007;
 
    // There are 0 ways for single post to
    // violate (same color_ and k ways to
    // not violate (different color)
    int same = 0, diff = k;
 
    // Fill for 2 posts onwards
    for (int i = 2; i <= n; i++) {
        // Current same is same as previous diff
        same = diff;
 
        // We always have k-1 choices for next post
        diff = total * (k - 1);
        diff = diff % mod;
 
        // Total choices till i.
        total = (same + diff) % mod;
    }
 
    return total;
}
 
// Driver code
int main()
{
    int n = 3, k = 2;
    cout << countWays(n, k) << endl;
    return 0;
}

Java

// Java program for Painting Fence Algorithm
class GFG {
 
    // Returns count of ways to color k posts
    // using k colors
    static long countWays(int n, int k)
    {
        // There are k ways to color first post
        long total = k;
        int mod = 1000000007;
 
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        int same = 0, diff = k;
 
        // Fill for 2 posts onwards
        for (int i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
 
            // We always have k-1 choices for next post
            diff = (int)total * (k - 1);
            diff = diff % mod;
 
            // Total choices till i.
            total = (same + diff) % mod;
        }
        return total;
    }
 
    // Driver code
    public static void main(String[] args)
    {
        int n = 3, k = 2;
        System.out.println(countWays(n, k));
    }
}
 
// This code is contributed by Mukul Singh

Python3

# Python3 program for Painting
# Fence Algorithm
 
# Returns count of ways to color
# k posts using k colors
def countWays(n, k) :
 
    # There are k ways to color first post
    total = k
    mod = 1000000007
 
    # There are 0 ways for single post to
    # violate (same color_ and k ways to
    # not violate (different color)
    same, diff = 0, k
 
    # Fill for 2 posts onwards
    for i in range(2, n + 1) :
         
        # Current same is same as
        # previous diff
        same = diff
 
        # We always have k-1 choices
        # for next post
        diff = total * (k - 1)
        diff = diff % mod
 
        # Total choices till i.
        total = (same + diff) % mod
     
    return total
 
# Driver code
if __name__ == "__main__" :
 
    n, k = 3, 2
    print(countWays(n, k))
 
# This code is contributed by Ryuga

C＃

// C# program for Painting Fence Algorithm
using System;
 
class GFG {
    // Returns count of ways to color k posts
    // using k colors
    static long countWays(int n, int k)
    {
        // There are k ways to color first post
        long total = k;
        int mod = 1000000007;
 
        // There are 0 ways for single post to
        // violate (same color_ and k ways to
        // not violate (different color)
        long same = 0, diff = k;
 
        // Fill for 2 posts onwards
        for (int i = 2; i <= n; i++) {
            // Current same is same as previous diff
            same = diff;
 
            // We always have k-1 choices for next post
            diff = total * (k - 1);
            diff = diff % mod;
 
            // Total choices till i.
            total = (same + diff) % mod;
        }
 
        return total;
    }
 
    // Driver code
    static void Main()
    {
        int n = 3, k = 2;
        Console.Write(countWays(n, k));
    }
}
 
// This code is contributed by DrRoot_

输出：

6