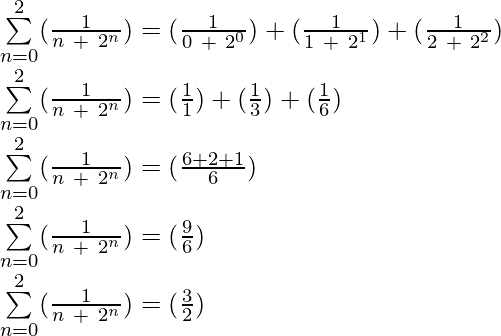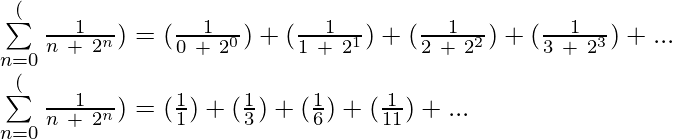序列和系列

在数学中，序列是数字的集合或列表，它们之间具有逻辑/顺序或模式。例如，1、5、9、13，…是在每个连续的下一个项之间相差4的序列，并且每个项可以以1 + 4 *(n – 1)的形式表示，其中n是该项的第n个项顺序。该序列可分为3类：

1. 算术序列
2. 几何序列
3. 调和序列

算术序列

每个连续项具有相同差且该差可以为正，负甚至为零的序列称为算术序列。

例子：

1) 0, 2, 4, 6, …   in this sequence each and every consecutive term has a difference of 2 between them and nth term of sequence can be represented as 2 * ( n – 1 ).

2) 0, 5, 10, 15, …  is another example of arithmetic sequence with a difference of 5 between each consecutive number and nth term of sequence can be represented as 5 * ( n – 1 ).

几何序列

每个连续项具有相同比率的序列称为几何序列。

例子：

1) 1, 5, 25, 125 … in this sequence, each consecutive term have a ratio of 5 with the term before it and nth term of sequence can be represented as 5 ^{( n – 1 )}.

2) 1, -2, 4, -8, 16, … in this sequence each consecutive term have a ratio of -2 with the term before it and nth term of sequence can be represented as ( -2 )^{( n – 1 )}.

调和序列

每个项的倒数形成算术序列的序列称为谐波序列。

例子：

(1/5), (1/10), (1/15), (1/20),… in this sequence the reciprocal of each term that is 5, 10, 15, 20, … forms an arithmetic sequence with a difference of 5 between each consecutive term.

什么是求和符号?

求和表示法是一种简单的查找序列之和的方法。求和表示法也称为sigma表示法。西格玛(Sigma)是指希腊字母西格玛(Σ)。序列的极限如图1所示，其中下限是序列的开始索引，上限是序列的结束索引。如图1所示，下限为1，上限为4，因此这意味着我们需要第一，第二，第三和第四项的总和，即(2 * 1)+(2 * 2)+(2 * 3)+(2 * 4)= 2 + 4 + 6 + 8 = 20。

汇总符号：

$\huge \sum\limits_{n=1}^4 (2*n)$

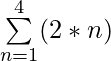
算术序列的求和符号

算术序列的和表示形式为Σ(a + b * n)，其中a是序列的第一项，b是序列的任何两个连续项之间的公共差，因此该序列的第n个项将是形式(a +(b * n))。

例子：

Let the arithmetic sequence be 0, 2, 4, 6, … so for making the summation notation we need to find the values of ‘a’ and ‘b’ where ‘a’ is the first term which is 0 so a = 0 and b is the common difference between any 2 consecutive terms which is 2 in this case, so b = 2.Therefore summation notion of sequence would be Σ (0 + (2 * n)) where the lower limit is 0 and the upper limit is ∞ as the first term of the sequence is given as 0 and ending is not defined.

算术求和符号：

$\huge \sum\limits_{n=0}^\infin (0\ +\ 2*n)$

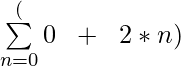
几何序列的求和符号

几何序列的和表示形式为Σ(a * b ⁿ )，其中a是序列的第一项，b是序列的任何两个连续项之间的公比，因此该序列的第n个项将是形式(a * b ⁿ )。

例子：

Let the geometric sequence be 2, 10, 50, 250, … so for making the summation notation we need to find the values of ‘a’ and ‘b’ where ‘a’ is the first term which is 2 so a = 2 and b is the common ratio between any 2 consecutive terms which is 5 in this case, so b = 5.Therefore summation notion of sequence would be Σ (2 * 5 ⁿ) where the lower limit is 0 and the upper limit is ∞ as the first term of the sequence is given as 0 and ending is not defined.

几何求和符号：

$\huge \sum\limits_{n=0}^\infin (2\ *\ 5^n)$

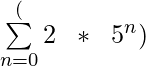
调和序列的加法表示法

调和序列的和表示形式为Σ(1 /(a + b * n))，其中a是序列的第一项的倒数，b是序列的任何两个连续项的倒数之间的公共差，因此，序列的第n个项的形式为(1 /(a + b * n))。

例子：

Let the arithmetic sequence be 1/2, 1/4, 1/6, … so for making the summation notation we need to find the values of ‘a’ and ‘b’ where ‘a’ is the reciprocal first term which is 2 so a = 2 and b is the common difference between the reciprocal of any 2 consecutive terms which is 2 in this case, so b = 2.Therefore summation notion of sequence would be Σ (1/( 0 + 2 * n)) where the lower limit is 1 and the upper limit is ∞ as the first term of the sequence is given as 1/2 and ending is not defined. 

谐波求和符号：

$\huge \sum\limits_{n=0}^\infin (\frac{1}{0\ +\ 2^n})$

例子

示例1：找到序列的前4个项：a _n = 2 * x ⁿ + 1且n> 0?

解决方案：

As we should take care to replace n ( and not x ) with the first 4 natural numbers as n is not equal to 0.

a₁ = 2 * x¹ + 1 

a₂ = 2 * x² + 1

a₃ = 2 * x³ + 1 

a₄ = 2 * x⁴ + 1

示例2：找到序列的前6个项：a _n = $\frac{1}{n\ +\ 2}$并且n≥0?

解决方案：

We have to replace n by the first 6 while numbers (0, 1, 2, 3, 4, 5).

a_{0 =} $\frac{1}{0\ +\ 2} = \frac{1}{\ 2}$

a_{1 =} $\frac{1}{1\ +\ 2} = \frac{1}{\ 3}$

a_{2 =} $\frac{1}{2\ +\ 2} = \frac{1}{\ 4}$

a_{3 =} $\frac{1}{3\ +\ 2} = \frac{1}{\ 5}$

a_{4 =} $\frac{1}{4\ +\ 2} = \frac{1}{\ 6}$

a_{5 =} $\frac{1}{5\ +\ 2} = \frac{1}{\ 7}$

示例3：评估$\sum\limits_{n=1}^k (2*n)$对于k = 2和k = 4?

解决方案：

For k = 2

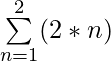$\sum\limits_{n=1}^2 (2*n)$ = (2 * 1) + (2 * 2) = 2 + 4 = 6 

For k = 4

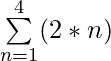$\sum\limits_{n=1}^4 (2*n)$ = (2 * 1) + (2 * 2) + (2 * 3) + (2 * 4) = 2 + 4 + 6 + 8 = 20 

示例4：评估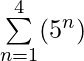$\sum\limits_{n=1}^4 (5^n)$ ?

解决方案：

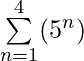$\sum\limits_{n=1}^4 (5^n)$ = (5¹) + (5²) + (5³) + (5⁴) = 5 + 25 + 125 + 625 = 780

示例5：评估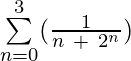$\sum\limits_{n=0}^3 (\frac{1}{n\ +\ 2^n})$ ?

解决方案：

$\sum\limits_{n=0}^2 (\frac{1}{n\ +\ 2^n})= (\frac{1}{0\ +\ 2^0})+(\frac{1}{1\ +\ 2^1})+(\frac{1}{2\ +\ 2^2})\\ \sum\limits_{n=0}^2 (\frac{1}{n\ +\ 2^n})=(\frac{1}{1})+(\frac{1}{3})+(\frac{1}{6})\\ \sum\limits_{n=0}^2 (\frac{1}{n\ +\ 2^n})=(\frac{6+2+1}{6})\\ \sum\limits_{n=0}^2 (\frac{1}{n\ +\ 2^n})=(\frac{9}{6})\\ \sum\limits_{n=0}^2 (\frac{1}{n\ +\ 2^n})=(\frac{3}{2})\\$

示例6：以扩展形式编写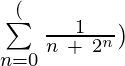： $\sum\limits_{n=0}^\infin (\frac{1}{n\ +\ 2^n})$最多4个学期?

解决方案：

$\sum\limits_{n=0}^\infin (\frac{1}{n\ +\ 2^n}) = (\frac{1}{0\ +\ 2^0}) + (\frac{1}{1\ +\ 2^1})+(\frac{1}{2\ +\ 2^2})+(\frac{1}{3\ +\ 2^3})+...\\ \sum\limits_{n=0}^\infin (\frac{1}{n\ +\ 2^n}) = (\frac{1}{1}) + (\frac{1}{3})+(\frac{1}{6})+(\frac{1}{11})+...$