第11类RD Sharma解决方案–第24章圈子–练习24.3

问题1.找到圆的方程，圆的端点的直径为(2，-3)和(-2，4)。找到它的半径和中心。

解决方案：

Given that the end points of the diameter are (2, -3) and (-2, 4).

So, the equation of the circle is

(x – 2)(x + 2) + (y + 3)(y – 4) = 0

x² – 4 + y² – y – 12 = 0

x² + y² – y – 16 = 0        ……(1)

From eq(1), we get

2g = 0, 2f = -1           

g = 0, f = -1/2 

The center of the circle is(0, 1/2) 

And 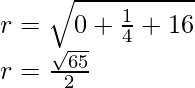$r=\sqrt{0+\frac{1}{4}+16}\\ r=\frac{\sqrt{65}}{2}$

问题2。找到圆的方程，其端点为圆的中心x ² + y ² + 6x – 14y – 1 = 0和x ² + y ² – 4x + 10y – 2 = 0。

解决方案：

Given equations are

x² + y² + 6x – 14y – 1 = 0

It can also written as

(x + 3)² + (y – 7)² = 59  ……(i)

x² + y² – 4x + 10y – 2y – 1 = 0

It can also written as

(x – 2)² + (y + 5)² = 31  ……(ii)

So, from eq(i) and (ii)

the centres of the circles are (-3, 7) and (2,-5)

Now the equation of the circle is  

(x – x1)(x – x2) + (y – y1)(y – y2) = 0

(x + 3)(x – 2) + (y – 7)(y + 5) = 0

x² + 3x – 2x – 6 + y² – 7y + 5y – 35 = 0

x² + y² + x – 2y – 41 = 0

问题3.正方形的边为x = 6，x = 9，y = 3和y =6。找到在正方形对角线上绘制的圆的方程式作为其直径。

解决方案：

Let us considered AB, BC, CD, and DA are the sides of the square ABCD be resented by the given equations  

y = 3, x = 6, y = 6 and x = 9 

So, the coordinates are

A(6, 3), B(9, 3), C(9, 6) and D(6, 6)

So, the equation of the circle with diagonal AC

(x – 6)(x – 9) + (4 – 3)(4 – 6) = 0

x² – 6x – 9x + 54 + y² – 3y – 6y + 18 = 0

x² + y² – 15x – 9y + 72 = 0

And the equation of the circle with diagonal BD as diameter is  

(x – 9)(x – 6) + (y – 3)(y – 6) = 0

x² – 9x – 6x + 54 + y² – 3y – 6y + 18 = 0

x² + y² – 15x – 9y + 72 = 0

x² + y² – 15 – 9y + 72 = 0

问题4.找到外接矩形的圆的方程，该矩形的边为x – 2y = 4、3x + y = 22，x – 3y = 14和3x + y = 62。

解决方案：

The given equations of the sides of the rectangle are

x – 3y = 4       ———– (i)

3x + y = 22    ———–(ii)

x – 3y = 14     ———–(iii)

3x + y = 62    ———-(iv)

Let us assume A, B, C, and D are the points intersection of the lines (i), (ii), (iii), and (iv)

So, A(7, 1), B(8, -2), C(20, 2) and D(19, 5)

AC will be the diameter of the circle

Hence, the equation of circle is

(x – 7)(x – 20) + (y – 1)(y – 2) = 0

x² + y² – 27x – 3y + 142 = 0

问题5。找到通过原点和线3x + 4y = 12与坐标轴相交的点的圆的方程。

解决方案：

Given equation of line is 3x + 4y = 12

So, it will meet the axis at A(0, 3) and B(4, 0)

Since the circle passes through origin A and B

So, AB is a diameter

Hence, the equation of circle is  

(x – 0)(x – 4) + (y – 3)(y – 0) = 0

x² + y² – 4x – 3y = 0

问题6：找到穿过原点并从x和y轴分别截取截距a和b的圆的方程。

解决方案：

It is given that the circle is passes through origin and cut intercept a and b on  

x-axis and y-axis

So, the coordinates of circle A(0, b) and B(a, 0)

Here, AB is the diameter of the circle

Hence, the equation of the circle is  

(x – a)(x – 0) + (y – 0)(y – b) = 0

x² + y² ± ax ± by = 0

问题7.找到直径为连接(-4，3)和(12，-1)的线段的圆的方程。还要找到它在y轴上所作的截距。

解决方案：

Given that the line segment A(-4, 3) and B(12, -1) is joining a diameter

So, the equation of circle in diameter form is,

(x + 4)(x – 12) + (y – 3)(y + 1) = 0

x² – 8x – 48 + y² – 2y – 3 = 0

x² – 8x – 2y + y² – 51 = 0 ……(1)

To find y-intercept, put x = 0 in eq(1), we get

y² – 2y – 51 = 0

$y=\frac{2±\sqrt{208}}{2}$

So, y intercepts are 1 ± 4√13

问题8.两点A和B的横坐标是等式x ² + 2ax – b ² = 0的根，它们的坐标是等式x ² + 2px – q ² = 0的根。以AB为直径的圆。另外，找到其半径。

解决方案：

The given equations are

x² + 2ax – b² = 0 ……..(i)

x² + 2px – q² = 0 ………(ii)

Now root of eq(i)

$x=\frac{-2a±\sqrt{4a^2+4b^2}}{2}=-a±\sqrt{a^2+b^2}$

and roots of eq(ii)

$x=\frac{-2p±\sqrt{4p^2+4q^2}}{2}=-p±\sqrt{p^2+q^2}$

So, the coordinates of A = ($-a+\sqrt{a^2+b^2},-p\sqrt{p^2+q^2}$)

and B = ($-a-\sqrt{a^2+b^2},-p-\sqrt{p^2+q^2}$)

So, the equation of circle is  

x² + y² + 2ax + 2py – (a² + b² + p² + q²) + a² + p² = 0

x² + y² + 2ax + 2py – (b² + q²) = 0

Hence, the radius is

$r=\sqrt{g^2+f^2-c}\\ =\sqrt{a^2+p^2-(b^2+q^2)}\\ =\sqrt{a^2+b^2+p^2+q^2}$

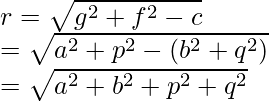
问题9. ABCD是一个以AB和AD为轴的边为a的正方形，证明外接该正方形的圆的方程为x ² + y ² – a(x + y)= 0。

解决方案：

Given that, ABCD is a square whose side is a.

Also, given that AD and AD are axes, so point of intersection is (0, 0)

Also, the other point on the diagonal of the square will have coordinates (a, a).

It is given that equation of the circle circumscribe the square.

So, (0, 0) and (a, a) will be the end points of the diameter of the circle.

So, the equation of the circle is 

(x – 0)(x – a) + (y – 0)(y – a) = 0

x² – ax + y² – ay = 0

x² + y² – a(x + y) = 0

问题10。2x – y + 6 = 0线与^{A和B处的圆x 2} + y ² – 2y – 9 = 0相遇。找到AB上圆的方程式作为直径。

解决方案：

The given equations of line and circle are

2x – y + 6 = 0        ……(i)

x² + y² – 2y – 9 = 0   …….(ii)

The point of intersection of eq (i) and (ii) is

x² + (2x + 6)² – 2(2x + 6) – 9 = 0

x² + 4x² + 24x + 36 – 4x – 12 – 9 = 0

5x² + 20x + 15 = 0

(x + 3)(x + 1) = 0                  

⇒ x = (-3, -1)

and  y = (0, 4)

So, point A(-3, 0) and B(-1, 4)

Here, AB is a diameter, so the equation of circle is

(x + 3)(x + 1) + (y – 0)(y – 4) = 0

x² + y² + 4x – 4y + 3 = 0

问题11。找到与由线x = 0，y = 0和lx + my = 1形成的三角形外接的圆的方程。

解决方案：

The given equations of lines are

x = 0   …….(i)

y = 0     …….(ii)

lx + my = 1   …….(iii)

The line eq(iii) cuts the axis at

A(0, 1/m) and B(1/l, 0)

Now, AB will be the diameter of circle,

So, the equation of circle will be,

(x – 1/l)(x – 0) + (y – 0)(y – 1/m) = 0

x² + y² – x/l – y/m = 0

问题12。从y = x和y = -x线中找到经过√2单位相等和弦的原点和切线的圆的方程。

解决方案：

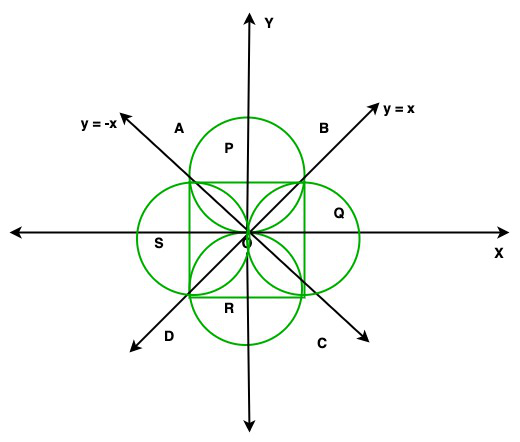
Let the angles between y = x and y = -x is π/2

So, the angle between OB and OA = π/2

Hence, AB, BC, CD and AD are diameter of circles.

so, ∠BOQ = π/4

sin∠BOQ = BQ/OB

sin π/4 = BQ/√2

1/√2 = BQ/√2

BQ = 1

So, the radius of circle(OQ) = 1 

And the coordinates of B is (1, 1)

Similarly, coordinates of A(-1, 1), C(1, -1), D(-1, -1)

Now the equation of circle with diameter AB is  

(x + 1)(x – 1) + (y – 1)(y – 1) = 0

x² – 2x + 1 + y² – 1 = 0

x² + y² – 2x = 0

The equation of circle with diameter BC is

(x – 1)(x – 1) + (y – 1)(y + 1) = 0

x² – 2x + 1 + y² – 1 = 0

x² + y² – 2x = 0

The equation of circle with diameter CD is  

(x + 1)(x – 1) + (y + 1)(y + 1) = 0

x² – 1 + y² + 2y + 1 = 0

x² + y² + 2y = 0

And the equation of circle with diameter AD is

(x + 1)(x + 1) + (y – 1)(y + 1) = 0

x² + 2x + 1 + y² – 1 = 0

x² + y² + 2x = 0