在数学中,我们知道函数是输入和输出之间的关系。在给定间隔的整个范围内,函数可以是递增,递减或恒定的,并且它们在给定间隔内是连续且可微的。现在,什么是间隔:因此,间隔被称为实线上的连续或连接的零件或部分。这种增加或减少的函数通常用于衍生物的应用中。因此,如果您想发现给定的函数在给定的时间间隔内正在增加或减少,则可以在导数的帮助下轻松找到它。
什么是递增,递减和常数函数?
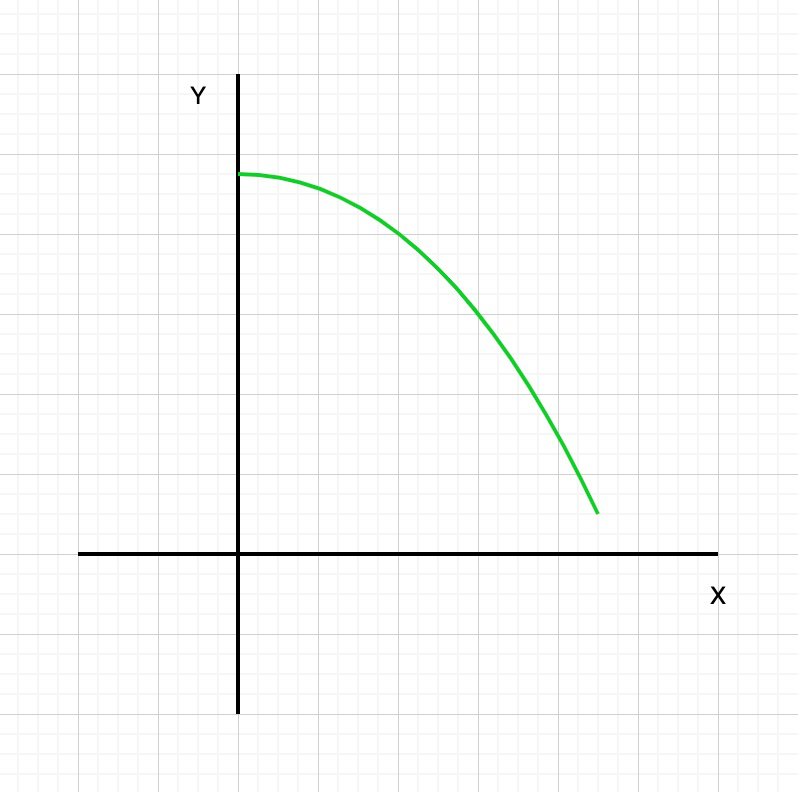
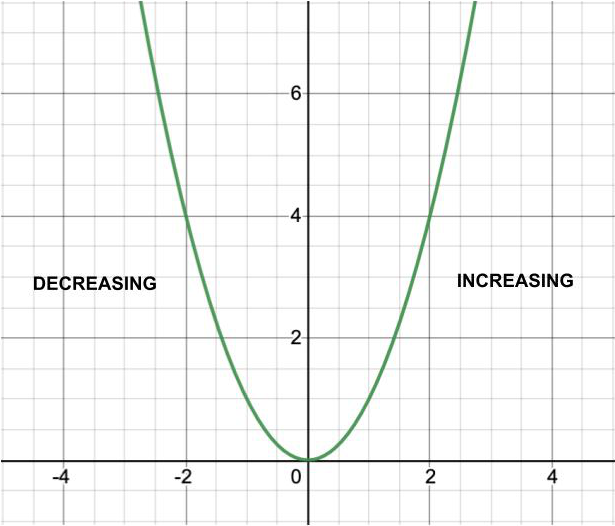
增加函数:当函数在给定间隔内增加时,这种函数类型称为增加函数。换句话说,当函数f(x)增大时,f(x)的值将随着x的增大而增大。或者,让我们认为我是一个存在于实值函数f的域中的区间。然后,将函数f在I增加,如果X1 递减函数:当函数在给定的间隔内递减时,这种类型的函数称为递减函数。换句话说,当函数f(x)是 减小,则f(x)的值随x的增加而减小。或者,让我们认为我是一个存在于实值函数f的域中的区间。然后 或者,就导数而言,当该点的导数为负时,函数将减小。递减函数的图形表示为: 常数函数:当函数在给定的间隔内既不增加也不减少时,则这种类型的函数称为常数函数。换句话说,当函数f(x)恒定时,f(x)的值不会随着x的增加而改变。 或者,让我们认为我是一个存在于实值函数f的域中的区间。如果f(x)= c∀x∈I,则函数f在I上是常数。在此,c是常数。或者,就导数而言,当导数为零时,函数是恒定的(即既不增加也不减少)。常数函数的图形表示为: Example: In this example, we will investigate the graph of f(x) = x2. Table: As we can see that when x < 0, the value of f(x) is decreasing as the graph moves to the right. In other words, the “height” of the graph is getting smaller. This is also confirmed by looking at the table of values. When x < 0, as x increases, f(x) decreases. Therefore, f(x) is decreasing on the interval from negative infinity to 0. When x > 0, the opposite is happening. When x > 0, the value of f(x) is increasing as the graph moves to the right. In other words, the “height” of the graph is getting bigger. This is also confirmed by looking at the table of values. When x > 0, as x increases, f(x) increases. Therefore, f(x) is increasing on the interval from 0 to infinity. 间隔增加和减少的属性 一些有用的代数性质: Theorem: Let us considered f be a function which is continuous on the interval[p, q] and differentiable on the open interval (p, q), Then Or A function y = f(x) is increasing on the interval (p, q) if and only if the first derivative of the function is positive for all x in the interval p < x < q. Similarly, a function y = f(x) is decreasing on the interval (p, q) if and only if the first derivative of the function is negative for all x in the interval p < x < q. 给定一个函数f(x),我们可以使用微分和代数来确定其递增和递减的间隔。 步骤1:找到该衍生物中,f’(x)时,该函数的。 步骤2:找出f’(x)的零点。请记住,零是f’(x)= 0的x的值。设置f’(x)= 0并求解x。 步骤3:确定间隔。间隔在f(x)的端点与f’(x)的零的端点之间。如果未给出f(x)的间隔,则假定f(x)在间隔(-∞,∞)上。 步骤4:确定函数在每个间隔上是增加还是减少。给定间隔(a,c),选择一个值b,a
Example 1: If g(x) = (x – 5)2, find the intervals where g(x) is increasing and decreasing. Step 1: Find the derivative of the function. Using the chain rule, g'(x) = 2(5 – x) Step 2: Find the zeros of the derivative function. In other words, find the values of for which g(x) equals zero. You can do this by setting g(x) = 0 and using algebra to solve for x. From the definitions above, we know the function is constant at points where the derivative is zero. g'(x) = 0 = 2(5 – x) 0 = 5 – x x = 5 Step 3: Use the zeros to determine intervals. Since x = 5 is the only zero for g'(x), there are just 2 intervals: from negative infinity to 5, and from 5 to negative infinity. These can be denoted in inequality notation: -∞ < x < 5 5 < x < ∞ Or in interval notation: (-∞, 5) (5, ∞) Remember, the endpoints are NOT inclusive because g(x) is neither increasing nor decreasing at the endpoints. Step 4: Determine if the function is increasing or decreasing in each interval. For the first interval, ((-∞, 5), we’ll choose b = 0. -∞ < x < 5 g'(b) = g'(0) = 2(5-0) = 10 10 > 0 POSITIVE For the second interval, (5, ∞), we’ll choose b = 6. 5 < 6 < ∞ g'(b) = g'(6) = 2(5-6) = -2 -2 < 0 NEGATIVE Therefore, g(x) is increasing on (-∞, 5) and decreasing on (5, ∞). We can verify our results visually. In the graph below, you can clearly see that f(x) = (x – 5)2 is increasing on the interval (5, ∞) and decreasing on the interval (-∞, 5). We can visually verify our result by investigating the graph of g(x). Looking at the graph, g(x) is indeed increasing in the interval from negative infinity to 5 and decreasing in the interval from 5 to infinity. Example 2: Find the intervals in -20 < x < 20 where g(x) is increasing and decreasing given g'(x) = x2 – 100. If the derivative is given, we can skip the first step and go straight to finding the zeroes. g'(x)= 0 = x2 – 100 x2 = 100 Intervals: (-20, -10), (-10, 10), (10, 20) For (-20, -10), we’ll choose b = -12. -20 < -12 < -10 g'(-12) = 44 > 0 For (-10, 10), we’ll choose b = 0. -10 < 0 < 10 g(0) = -100 < 0 For (10, 20), we’ll choose b = 12. 10 < 12 < 20 g(12) = 44 > 0 Hence, for -20 < x < 20, g(x) is increasing on (-20, -10) and (10, 20) and decreasing on (-10, 10). We can find g(x) by integrating the given g'(x). Thus, 问题1.给定函数g(x)= 3x 2 – 12,找到-3 解决方案: Given function: g(x) = 3x2 – 12 Differentiate w.r.t. x, we get g'(x) = 6x For increasing and decreasing Put g'(x) = 0 g'(x) = 6x = 0 So, x = 0 Intervals: (-3, 0), (0, 3) At x = -2, g'(-2) = -12 < 0 At x = 2, g'(2) = 12 > 0 So, for -3 < x < 3, g(x) is decreasing on (-3, 0) and increasing on (0, 3). 问题2.给定f(x)的导数,f’(x)= -10x 2 + 40x,找出f(x)递增和递减的区间。 解决方案: Given: f'(x) = -10x2 + 40x For increasing and decreasing Put f'(x) = 0 f'(x) = -10x2 + 40x = 0 So, x = 4, 0 Intervals: (−∞, 0), (0, 4), (4, ∞) So, at x = -1, f'(-1) = -50 < 0 at x = 1, f'(1) = 30 > 0 at x = 5, f'(5) = -50 < 0 So, f(x) is increasing on (0, 4) and decreasing on (−∞, 0), (4, ∞) 问题3.给定函数g(x)= 5x 2 – 20x + 100,找到g(x)递增和递减的间隔。 解决方案: Given: g(x) = 5x2 – 20x + 100 Differentiate w.r.t. x, we get g'(x) = 10x – 20 For increasing and decreasing Put g'(x) = 0 g'(x) = 10x – 20 = 0 x = 2 Intervals: (−∞, 2), (2, ∞) At, x = 1, g'(1) = -10 < 0 At x = 3, g'(3) = 10 > 0 So, g(x) is decreasing on (-∞, 2) and increasing on (2, ∞) 问题4.给定函数s(x)= 6x 3 – x 2 ,找到0 解决方案: Given: s(x) = 6x3 – x2 Differentiate w.r.t. x, we get s'(x) = 18x2 – 2x For increasing and decreasing Put s'(x) = 0 s'(x) = 18x2 – 2x = 0 x = 1/9, -1/9 Intervals: (0, 1/9) Here, -1/9 is not in the given interval, 0 < x < 10 So, g'(1/10) = -0.02 < 0 Hence, for 0 < x < 10, g(x) is decreasing on (0, 1/9) 问题5.给定g’(x)= 7x 2 – 8,求出g(x)递增和递减的间隔。 解决方案: Given: g'(x) = 7x2 – 8 For increasing and decreasing Put g'(x) = 0 g'(x) = 7x2 – 8 = 0 x = Intervals: So, At x = -10, g'(-10) = 692 > 0 At x = 0, g'(0) = -8 < 0 At x = 10, g'(10) = 692 < 0 Hence, g(x) is increasing on 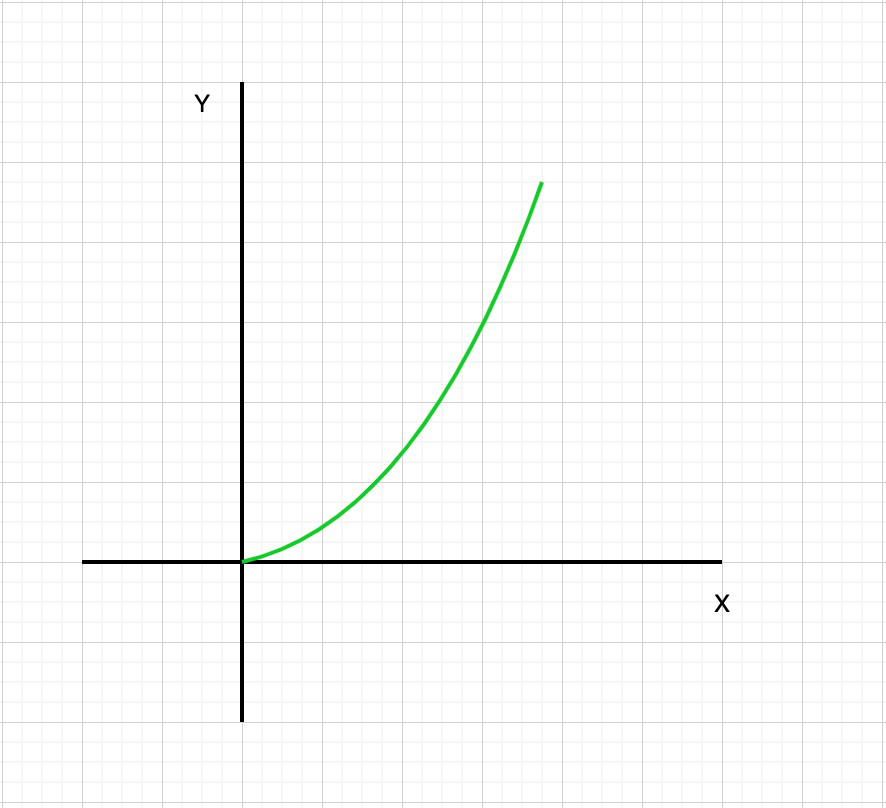
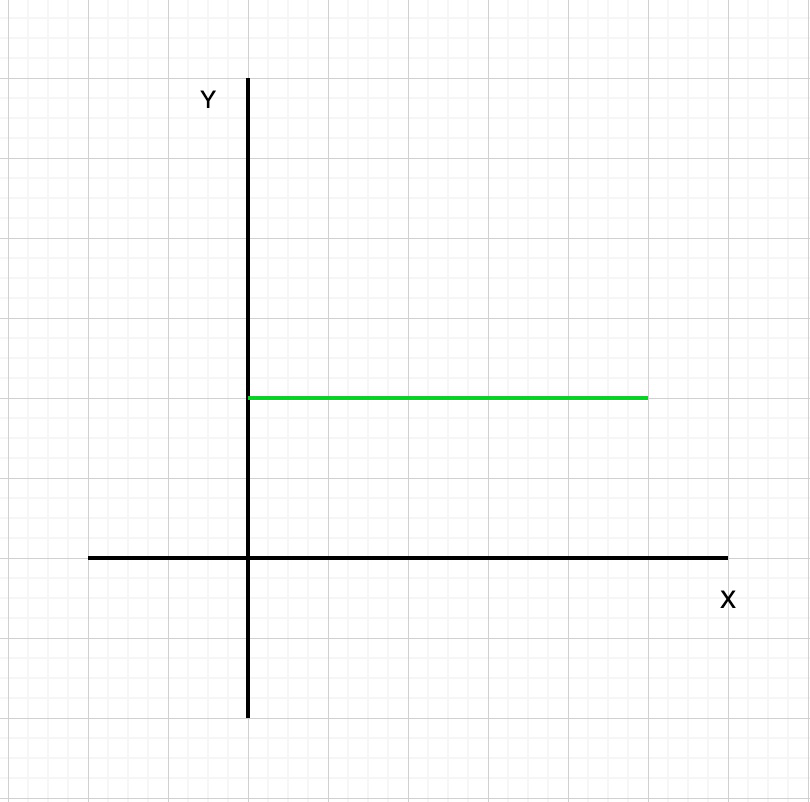
x
f(x)
-4
16
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
4
16
查找间隔增大和减小
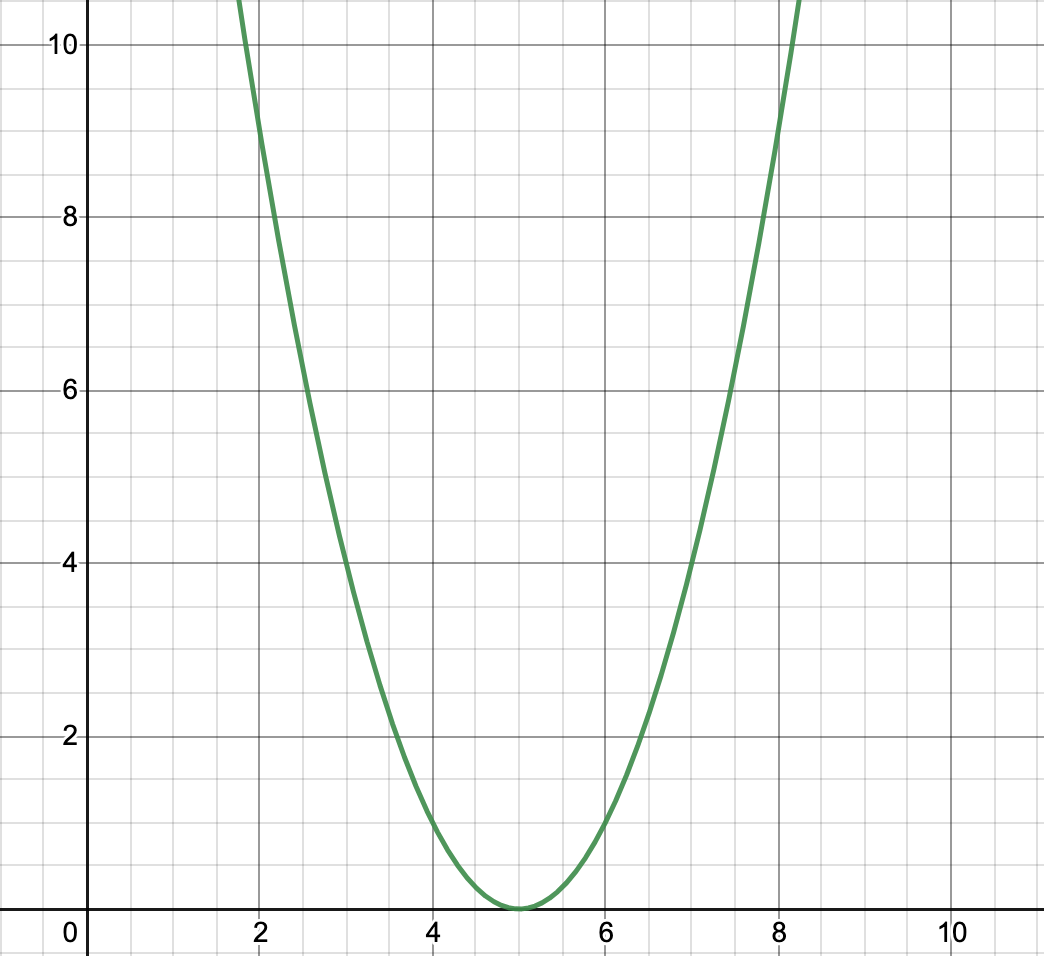
![]()
![]() . Looking at the graph, g(x) is indeed increasing in the interval from -20 to -10 and the interval from 10 to 20 and decreasing in the interval from -10 to 10.
. Looking at the graph, g(x) is indeed increasing in the interval from -20 to -10 and the interval from 10 to 20 and decreasing in the interval from -10 to 10. 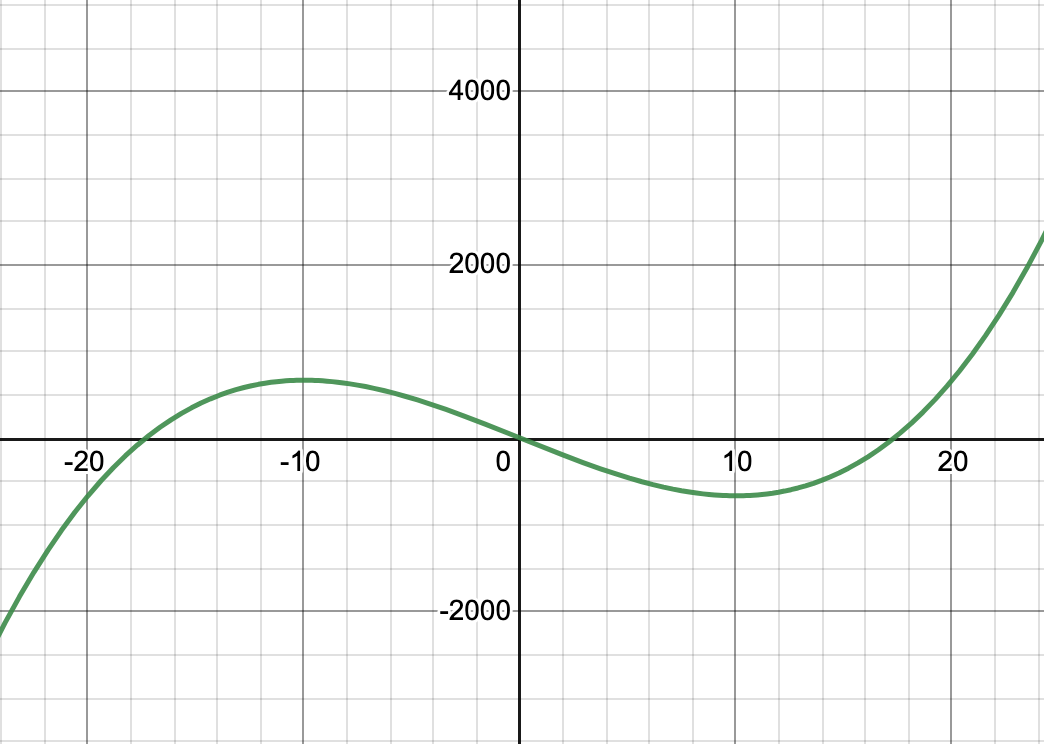
样本问题
![]()
![]()
![]() and
and ![]() , and decreasing on
, and decreasing on ![]()