第12类RD Sharma解决方案–第18章，最大值和最小值–练习18.5 |套装2

问题16.大窗户的形状是矩形，上面有一个等边三角形。如果窗口的周长为12米，请找到将产生窗口最大面积的矩形的尺寸。

解决方案：

According to the question

Let us assume l be the length of the rectangle and b be the breadth of the rectangle

The perimeter of the window = 12 m

⇒ (l + 2b) + (l + l) = 12

⇒ 3l + 2b = 12     ……(i)

Mow we find the area of the window (A) = Area of the rectangle + Area of the equilateral △

A = l (12 – 3l / 2) + √3/4 l²

On differentiating w.r.t. l, we get

dA/dl = 6 – 3l + (√3/2)l = 6 – √3(√3 – 1/2)l

For maxima and minima,

Put dA/dl = 0

⇒ 6 – √3(√3 – 1/2)l = 0

⇒ l = 6/{√3(√3 – 1/2) } = 12- (6 – √3)

Now, d²A/dl² = -√3(√3 – 1/2) = -3 + √3/2

So, l = 12/(6 – √3) is the point of local maxima

So, When l = 12/(6 – √3), the area of the window is maximum

From eq(i), we get

b = (12 – 3l)/2 = [12 – 3{12/(6 – √3)}]/2 = (24 – 6√3)/(6 – √3)

问题17：证明可以在半径为R的球体内切出的最大容积圆柱体的高度为2R /√3。另外，找到最大音量。

解决方案：

According to the question

R be the radius of the sphere 

So, let us assume that r and h be the radius and the height of the cylinder 

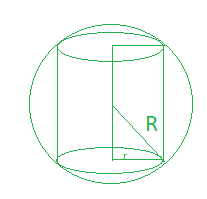
So, according to the image

h = 2 √(R² – r²)

Now we find the volume of the cylinder is 

V = πr²h = 2πr²√(R² – r²)

On differentiating w.r.t. r, we get

dV/dr = 4πr √(R² – r²) + $\frac{2πr^2(-2r)}{2\sqrt{R^2-r^2}}$

= 4πr √(R² – r²) – $\frac{2πr^3}{2\sqrt{R^2-r^2}}$

= $\frac{4πr(R^2-r^2)-2πr^3}{\sqrt{R^2-r^2}}$

= $\frac{4πrR^2-6πr^3}{\sqrt{R^2-r^2}}$

For maxima and minima,

Put dV/dr = 0  

4πrR² – 6πr³ = 0

r² = 2R²/3

Now, again differentiating w.r.t. r, we get

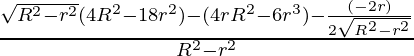
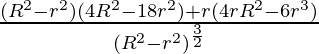
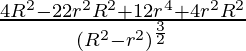
d²V/dr² = $\frac{\sqrt{R^2-r^2}(4πR^2-18πr^2)-(4πrR^2-6πr^3)-\frac{(-2r)}{2\sqrt{R^2-r^2}}}{R^2-r^2}$

= $\frac{(R^2-r^2)(4πR^2-18πr^2)+r(4πrR^2-6πr^3)}{(R^2-r^2)^\frac{3}{2}}$

= $\frac{4πR^2-22πr^2R^2+12πr^4+4πr^2R^2}{(R^2-r^2)^\frac{3}{2}}$

So, at r² = 2R²/3, d²V/dr² < 0

Hence, the volume is the maximum when r² = 2R²/3

so, the height of the cylinder = 2√(R² – 2R²/3) = 2√(R²/3) = 2R/√3

Hence proved

问题18：在半径为r的半圆中刻有一个矩形，其矩形的边之一为半圆的直径。找到矩形的尺寸，以便其最大面积。同时找到该面积。

解决方案：

Let us assume EFGH be a rectangle inscribed in a semi-circle. So, r be the radius of the semicircle.

And l and b are the length and width of rectangle.

Now In △OHE, 

HE² = OE² – OH²

HE = b = $\sqrt{r^2-(\frac{l}{2})^2}$  …..(i)

Now we find the area of the EFGH rectangle

A = lb = l × $\sqrt{r^2-(\frac{l}{2})^2}$

A = 1/2 l √(4r² – l²)

On differentiating w.r.t. l, we get

dA/dl = 1/2 \sqrt{4r^2-l^2}-\frac{l^2}{\sqrt{4r^2-l^2}}

= 1/2 \frac{4r^2-l^2-l^2}{\sqrt{4r^2-l^2}}

= $\frac{2r^2-l^2}{\sqrt{4r^2-l^2}}$

For maxima and minima,

Put dA/dl = 0

⇒ $\frac{2r^2-l^2}{\sqrt{4r^2-l^2}} = 0$

⇒ l = ±√2r

As we know that l can’t be negative so l ≠ -√2r

So, when l = √2r, d²A/dl² < 0 

Hence, the area of the rectangle is maximum when l = √2r

Now put the value of l = √2r in eq(i), we get

$b=\sqrt{r^2-(\frac{l}{2})^2}=\frac{r}{√2}$

Now we find the area of rectangle = lb 

= √2r × r/√2   

= r²

问题19.证明当高度为基部半径的√2倍时，给定容量的圆锥形帐篷所需的帆布量最少。

解决方案：

Let us assume that the radius and height of the cone is r and h.

So, the volume of the cone is 

V = 1/3 πr²h  

h = 3V/r²  ……(i)

And the surface area of the cone is 

A = πrl 

Here, l is the slant height = √(r² + h²)

= πr√(r² + h²)

= $πr\sqrt{r^2+\frac{9V^2}{π^2r^4}}=1/r.\sqrt{π^2r^6+9V^2}$

On differentiating w.r.t. r, we get

dA/dr = 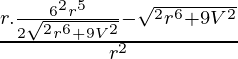$\frac{r.\frac{6π^2r^5}{2\sqrt{π^2r^6+9V^2}}-\sqrt{π^2r^6+9V^2}}{r^2}$

= $\frac{2π^2r^6-9V^2}{r^2\sqrt{π^2r^6+9V^2}}$

For maxima and minima,

Put dA/dr = 0 

2π²r⁶ = 9V² 

r⁶ = 9V²/2π²

When, r⁶ = 9V²/2π², d²S/dr² > 0

Hence, the surface area of the cone is the least when r⁶ = 6V²/2π²

Now put r⁶ = 9V²/2π² in eq(i), we get

h = 3V/πr² = 3/πr²(2π²r⁶/9)^1/2 = (3/πr²)(√2πr³/3) = √2r

Hence Proved

问题20：证明在给定球体中可以接切的最大体积的圆锥体的高度等于球体直径的2/3。

解决方案：

Let us assume R be the radius of the sphere

So, from the figure, we get OD = x and AO = OB = R

BD = √(R² – x²) and AD = (R + x)

Now, 

The volume of the cone is 

V = 1/3 πr²h

= 1/3 πBD² × AD

= 1/3 π (R² – x²) × (R + x)

On differentiating w.r.t. x, we get

dV/dx = π/3 [-2x (R + x) + R² – x²]

= π/3 [R² – 2xR – 3x²]

For maximum and minimum

Put dv/dx = 0

⇒ π/3 [R²– 2xR – 3x²] = 0

⇒ π/3 [(R – 3x) (R + x)] = 0

⇒ R  – 3x = 0 or x = -R

Here, x = -R is not possible because -r will make the altitude 0

⇒ x = R/3            

Now,

d²V/dx² = π/3[-2R – 6x]

So, when x = R/3, d²v/dx² = π/3[-2R – 2R] = -4πR/3 < 0

So, x = R/3 is the point of local maxima.

Hence, the volume is maximum when x = R/3

So, the altitude AD = (R + x) = (R + R/3) = 4R/3 = 2/3d

Here, d is the diameter of sphere.

问题21：证明给定体积和最小曲面的右圆锥体的半垂直角为cot ^-1 (√2)。

解决方案：

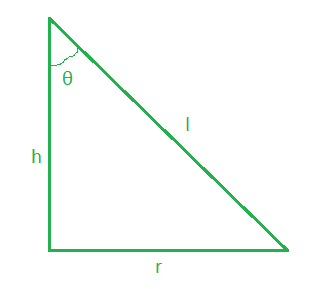
Let us assume h, r and θ be the height, radius and semi vertical angle of the right-angled triangle.

So, the volume of the cone (V) = 1/3 πr²h

⇒ h = 3V/πr²

Slant height of the cone (l) = √(r² + h²)

l = $\frac{\sqrt{π^2r^6+9V^2}}{πr^2}$

And the curved surface area of the cone is 

A = πrl

A = πr$\frac{\sqrt{π^2r^6+9V^2}}{πr^2}$

A = $\frac{\sqrt{π^2r^6+9V^2}}{r}$

On differentiating w.r.t. r, we get

dA/dr = 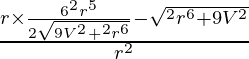$\frac{r \times \frac{6π^2r^5}{2\sqrt{9V^2 +π^2r^6 }}-\sqrt{π^2r^6+9V^2}}{r^2}$ 

= $\frac{2\pi^2r^6-9V^2}{r^2\sqrt{9V^2+\pi^2r^6}}$

For maximum and minimum

Put dA/dr = 0

$\frac{2\pi^2r^6-9V^2}{r^2\sqrt{9V^2+\pi^2r^6}}$ = 0

⇒ 2π²r⁶ – 9V² = 0

⇒ V² = 2π²r⁶/9

⇒ V = √2π²r⁶/9

⇒ V = πr³√2/3

0r 

r = (3V/π√2)^1/3

h/r = √2

cotθ = √2

Semi-vertical angle, θ = cot^-1√2

Also, when r < (3V/π√2)^1/3, dA/dr < 0

When r > (3V/π√2)^1/3, dA/dr > 0

Hence, the curved surface for r = (3V/π√2)^1/3 is least.

问题22半径为a的圆内切有一个垂直角为2θ的等腰三角形。证明当θ=π/ 6时三角形的面积最大。

解决方案：

Let us considered ABC is an isosceles triangle such that AB = AC

and the vertical angle∠BAC = 2θ

Radius of the circle = a

Now, draw AM perpendicular to BC.

From the figure we conclude that in △ABC is an isosceles triangle 

the circumcentre of the circle lies on the perpendicular from A to BC and 

O be the circumcentre of the circle

So, ∠BOC = 2 × 2θ = 4θ

and ∠COM = 2θ   [Since △OMB and △OMC are congruent triangles]

OA = OB = OC =a       [Radius of the circle]

In △OMC,

CM = asin2θ and OM = acos2θ

BC = 2CM  [Perpendicular from the centre bisects the chord]

BC = 2asin2θ                             …..(i)

In △ABC,

AM = AO + OM

AM = a + acos2θ                          …..(ii)

Now the area of △ABC is,

A = 1/2 × BC × AM

= 1/2 × 2asin2θ × (a + acos2θ)   ……(iii)

On differentiating w.r.t. θ, we get

dA/dθ = a²(2cos2θ + 1/2 × 4cos4θ)

dA/dθ = 2a² (cos2θ + cos4θ)

Again differentiating w.r.t. θ, we get

d²A/dθ² = 2a²(-2sin2θ – 4sin4θ)

For maximum and minimum

Put dA/dθ = 0

2a²(cos2θ + cos4θ) = 0

cos2θ + cos4θ = 0

cos2θ + 2cos²2θ – 1 = 0

(2cos2θ – 1)(2cos2θ + 1) = 0

cos2θ = 1/2 or cos2θ = -1

2θ = π/3 or 2θ = π

θ = π/6 or θ = π/2

When θ = π/2, it will not form a triangle.

When θ = π/6, d²A/dθ² < 0

Hence, the area of the triangle is maximum when θ = π/6

问题23。找到周长36厘米的矩形的尺寸，当绕其一侧旋转时，该矩形将扫出尽可能大的体积。

解决方案：

Let us assume l, b, and V be the length, breadth, and volume of the rectangle.

The perimeter of the rectangle is 36cm

2(l + b) = 36

l + b = 18

l = 18 – b ……(i)

The volume of the cylinder that revolve about the breadth, 

V = πl²b

V = π(18 – b )²b

V = π(324 + b² – 36b)b

V = π(324b + b³ – 36b²)

On differentiating w.r.t. b, we get

dV/db = π(324 + 3b² – 72b)

Again differentiating w.r.t. b, we get

d²V/db² = π(6b – 72)

For maximum and minimum

Put dV/db = 0

 π(324b + b³ – 36b²) = 0

(b – 6)(b – 18) = 0

b = 6, 18

When b = 6, d²V/db² = -36π < 0

When b = 18, d²V/db² = 36π > 0

So, at b = 6 is the maxima

Hence, the volume is maximum when b = 6

Now put the value of b in eq(i), we get

l = 18 – 6

l = 12

Hence, the dimension of rectangle are 12 cm and 6 cm.

问题24.证明可以在半径为12 cm的球体中内接的最大体积圆锥的高度为16 cm。

解决方案：

Let us assume r and h be the radius of the base of cone and height of the cone.

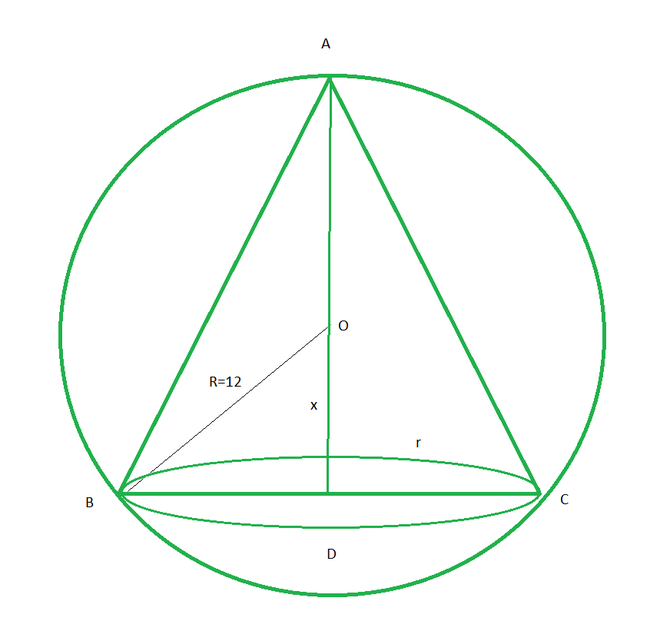
From the figure OD = x, and R = 12, BD = r

In △BOD,   

BD = √(R² – x²)

= √(144 – x²)

= (144 – x²)

and AD = AO + OD 

= R + x = 12 + x

The volume of cone is 

V = 1/3 πr²h

= 1/3 π BD² × AD

= 1/3 π(144 – x²)(12 + x)

= 1/3 π(1728 + 144x – 12x² – x³)

On differentiating w.r.t. x, we get

dV/dx = 1/3π (144 – 24x – 3x²)

For maximum and minimum

Put dV/dx = 0

⇒ 1/3 π(144 – 24x – 3x²) = 0

⇒ x = -12, 4

Here x = -12 is not possible

So, x = 4

Now, 

d²V/dx² = π/3(-24 – 6x)

At x = 4, d²v/dx² = -2π(4 + x) = -2π × 8 = -16π < 0

So, x = 4 is point of local maxima.

Hence, the height of cone of maximum volume = R + x

= 12 + 4 = 16 cm

问题25.一个封闭的圆柱体的容积为2156 cm ³ 。底面的半径是多少，以使其总表面积最小?

解决方案：

Given that the volume of the closed cylinder (V) = 2156 cm³

Let us assume r and h be the radius and the height of the cylinder. 

So, the volume of the cylinder is 

V= πr²h = 2156              …..(i)

and the total surface area is 

A = 2πrh + 2πr²

A = 2πr (h + r)        …..(ii)

So, from eq (i) and (ii)

A = (2156 × 2)/r + 2πr²

On differentiating w.r.t. r, we get

dA/dr = – 4312/4π + 4πr

For maximum and minimum

Put dA/dr = 0

⇒ (-4312 + 4πr³)/r² = 0

⇒ r³ = 4312/4π

⇒ r = 7

At r = 7, d²s/dr² = (8624/r3 + 4π) > 0 

So, r = 7 is the point of local minima

Hence, the total surf surface area of closed cylinder will be minimum when r = 7 cm.

问题26.证明可以在半径为5√3cm的球体内切入的圆柱的最大体积为500πcm ³ 。

解决方案：

Let r and h be the radius and height of the cylinder.

Given that R be the radius of the sphere = 5√3 

So, from the figure LM = h, OL = x

So, h = 2x

Now, In △AOL, 

AL = √(AO² – OL²)

= √(75 – x²)

As we know that the volume of cylinder is 

V = πr²h

= πAL² × ML

= π(75 – x²) × 2x

On differentiating w.r.t. x, we get

 dV/dx = π[150 – 6x²]

For maximum and minimum

Put dV/dx = 0 

⇒ π[150 – 6x²] = 0

⇒ x = 5 cm

Also, d²v/dx² = -12πx

At x = 5, d²v/dx² = -60πx < 0

So, x = 5 is point of local maxima.

Hence, the volume is maximum when x = 5

So, the maximum volume of cylinder is 

= π(75 – 25) × 10 = 500π cm³

^{问题27.证明在x 2}和y ² = r ^2的所有正数x和y中，当x = y = r /√2时，总和x + y最大。

解决方案：

Let us considered the two positive numbers are x and y with

x²+y² = r²     ……(i)

Let S be the sum of two positive numbers

S = x + y   …..(ii)

= x + √(r² – x²)       [From eq(ii)]

On differentiating w.r.t. x, we get

dS/dx = 1 –  x/√(r² – x²)

For maximum and minimum

Put dS/dx = 0

⇒ 1 – x/√(r² – x²) = 0

⇒ x = √(r² – x²)

⇒ 2x² = r²

⇒ x = r/√2, -r/√2

According to the question x and y are the positive numbers 

So, x ≠ -r/√2  

 Now, d²S/dx² = 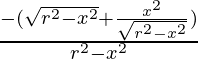$\frac{-(\sqrt{r^2-x^2}+\frac{x^2}{\sqrt{r^2-x^2}})}{{r^2-x^2}}$

 At, x = r/√2, d²S/dx²= $[\frac{\frac{r}{√2}+\frac{\frac{r^2}{2}}{\frac{r}{√2}}}{\frac{r^2}{2}}]$ < 0

So, x = r/√2 is point of local maxima.

Hence, the sum is largest when x = y = r/√2

问题28.确定曲线x ² = 4y上最接近点(0，5)的点。

解决方案：

The given equation of parabola is

x² = 4y  …….(i)

Let us considered P(x, y) be the nearest point of the given parabola from the point A (0, 5)

Let Q be the square of the distance of P from A

Q = x² + (y – 5)²        …..(ii)

Q = 4y + (y – 5)²

On differentiating w.r.t. y, we get

⇒ dQ/dy = 4 + 2(y – 5)

For maximum and minimum

Put dQ/dy = 0 

⇒ 4 + 2(y – 5) = 0

⇒ 2y = 6

⇒ y = 3

From eq(i), we get

x² = 12

x = 2√3

⇒ P = (2√3, 3) and p’ = (-2√3, 3)

Now, 

d²Q/dy² = 2 > 0

So, P and P’ are the point of local minima.

Hence, the nearest points are P(2√3, 3) and P”(2√3, 3).

问题29.在曲线y ² = 4x上找到最接近点(2，-8)的点。

解决方案：

The given equation of the curve is 

y² = 4x ….(1)

Let us assume P(x, y) be a point on the given curve and 

Q be the square of the distance between A(2,-8) and P.

So, Q = (x – 2)² + (y + 8)²   …….(ii)

= (y²/4 – 2)² + (y + 8)²

On differentiating w.r.t. y, we get

dQ/dy = 2(y²/4 – 2) × y/2 + 2(y + 8)

= (y³ – 8y)/4 + 2y + 16

= y³/4 + 16

For maximum and minimum

Put dQ/dy = 0 

⇒ y³/4 + 16 = 0

⇒ y = -4

Now,

d²Q/dy² = 3y²/4

At y = -4, d²S/dy² = 12 > 0

Ao, y = -4 is the point of local minima

Now put the value of y in eq(i), we get

x = y²/4 = 4

Hence, the point is(4, -4) which is nearest to (2, -8).

问题30.在曲线x ² = 8y上找到最接近点(2，4)的点。

解决方案：

The given equation of the curve is 

 x² = 8y   ….(1)

Let P(x, y) be a point on the given curve, and 

Q be the square of the distance between P and A(2, 4). 

Q = (x – 2)² + (y – 4)²   ……..(ii)

= (x – 2)² + (x²/8 – 4)²

On differentiating w.r.t. x, we get

dQ/dx = 2(x – 2) + 2(x²/8 – 4) × 2x/8

= 2(x – 2) + (x² – 32)x/16

Also, d²Q/dx² = 2 + 1/16[x² – 32 + 2x²]

= 2 + 1/16[3x² – 32]

For maxima and minima,

dQ/dx = 0

⇒ 2(x – 2) + x(x² – 32)/16 = 0

⇒ 32x – 64 + x³ -32x = 0

⇒ x³ – 64 = 0

⇒ x = 4

At x = 4, d²Q/dx² = 2 + 1/16[16 × 3 – 32] = 2 + 1 = 3 > 0

So, x = 4 is point of local minima

Now put the value of x in eq(1), we get

y = x²/8 = 2

So, the P(4, 2) is the nearest point to (2, 4)