使用一阶导数检验,找到以下函数的局部最大值或局部最小值的点。此外,视情况而定,找到局部最大值或局部最小值:
问题1. f(x)=(x – 5) 4
解决方案:
Given function
f(x) = (x – 5)4
Now, differentiate the given function w.r.t. x
f ‘(x) = 4(x-5)3
Now, for local maxima and minima
Put f ‘(x) = 0
⇒ 4(x – 5)3 = 0
⇒ x – 5 = 0
⇒ x = 5
So, at x = 5, f'(x) changes from negative to positive. Hence, x = 5 is the point of local minima
So, the minimum value is f(5) = (5 – 5)4 = 0
问题2。f(x)= x 3 – 3x
解决方案:
Given function
f(x) = x3– 3x
Now, differentiate the given function w.r.t. x
f ‘(x) = 3x2– 3
Now, for local maxima and minima
Put f ‘(x) = 0
⇒ 3x2– 3 = 0
⇒ x = ±1
Now, again differentiating f'(x) function w.r.t. x
f “(x) = 6x
Put x = 1 in f”(x)
f “(1)= 6 > 0
So, x = 1 is point of local minima
Put x = -1 in f”(x)
f “(-1)= -6 < 0
So, x = -1 is point of local maxima
So, the minimum value is f(1) = x3– 3x = 13 – 3 = -2
and the maximum value is f(-1) = x3– 3x = (-1)3 – 3(-1) = 2
问题3。f(x)= x 3 (x – 1) 2
解决方案:
Given function
f(x) = x3(x – 1)2
Now, differentiate the given function w.r.t. x
f ‘(x) = 3x2 (x- 1)2 + 2x3(x- 1)
= (x – 1) (3x2(x – 1) + 2x3)
= (x – 1) (3x3 – 3x2 + 2x3)
= (x – 1) (5x3 – 3x2)
= x2(x – 1) (5x – 3)
Now, for all maxima and minima,
Put f ‘(x) = 0
= x2(x – 1) (5x- 3) = 0
x = 0, 1, 3/5
So, at x = 3/5, f'(x) changes from negative to positive. Hence, x = 3/5 is a point of minima
So, the minimum value is f(3/5) = (3/5)3(3/5 – 1)2 = 108/3125
At x = 1, f'(x) changes from positive to negative. Hence, x = 1 is point of maxima.
So, the maximum value is f(1) = (1)3(1 – 1)2 = 0
问题4. f(x)=(x – 1)(x + 2) 2
解决方案:
Given function
f(x) = (x – 1)(x + 2)2
Now, differentiate the given function w.r.t. x
f ‘(x) = (x + 2)2 + 2(x – 1)(x + 2)
= (x+ 2) (x+ 2 + 2x – 2)
=(x + 2) (3x)
Now, for all maxima and minima,
Put f ‘(x) = 0
⇒ (x + 2) (3x) = 0
x = 0,-2
So, at x = -2, f(x) changes from positive to negative. Hence, x = -2 is a point of Maxima
So, the maximum value is f(-2) = (-2 – 1)(-2 + 2)2 = 0
At x = 0, f ‘(x) changes from negative to positive. Hence, x = 0 is point of Minima.
So, the minimum value is f(0) = (0 – 1)(0 + 2)2 = -4
问题5. f(x)=(x – 1) 3 (x + 1) 2
解决方案:
Given function
f(x) = (x – 1)3 (x + 1)2
Now, differentiate the given function w.r.t. x
f ‘(x) = 3(x – 1)2 (x + 1)2 + 2(x – 1)3 (x + 1)
= (x – 1)2 (x + 1) {3(x + 1) + 2(x – 1)}
= (x – 1)2 (x + 1) (5x + 1)
Now, for local maxima and minima,
Put f ‘(x) = 0
⇒ (x – 1)2 (x + 1) (5x + 1) = 0
⇒ x = 1, -1, -1/5
So, at x = -1, f ‘(x) changes from positive to negative. Hence, x = -1 is point of maxima
So, the maximum value is f(-1) = (-1 – 1)3 (-1 + 1)2 = 0
At x = -1/5, f ‘(x) changes from negative to positive so x= -1/5 is point of minima
So, the minimum value is f(-1/5) = (-1/5 – 1)3 (-1/5 + 1)2 = -3456/3125
问题6. f(x)= x 3 – 6x 2 + 9x +15
解决方案:
Given function
f(x) = x3 – 6x2 + 9x + 15
Now, differentiate the given function w.r.t. x
f ‘(x) = 3x2 – 12x + 9
= 3 (x2 – 4x + 3)
= 3 (x – 3) (x – 1)
Now, for local maxima and minima,
Put f ‘(x) = 0
⇒ 3 (x – 3) (x – 1) – 0
⇒ x = 3, 1
At x = 1, f'(x) changes from positive to negative. Hence, x = 1 is point of local maxima
So, the maximum value is f(1) = (1)3 – 6(1)2 + 9(1) + 15 = 19
At x = 3, f'(x) changes from negative to positive. Hence, x = 3 is point of local minima
So, the minimum value is f(x) = (3)3 – 6(3)2 + 9(3) + 15 = 15
问题7. f(x)= sin2x,0
解决方案:
Given function
f(x) = sin2x, 0 < x, π
Now, differentiate the given function w.r.t. x
f'(x) = 2 cos 2x
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 2x = 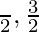
⇒ x = 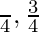
At x = π/4, f'(x) changes from positive to negative. Hence, x = π/4, Is point of local maxima
So, the maximum value is f(π/4) = sin2(π/4) = 1
At x = 3π/4, f'(x) changes from negative to positive. Hence, x = 3π/4 is point of local minima,
So, the minimum value is f(3π/4) = sin2(3π/4) = -1
问题8. f(x)= sin x – cos x,0
解决方案:
Given function
f(x) = sin x – cos x, 0 < x < 2π
Now, differentiate the given function w.r.t. x
f'(x)= cos x + sin x
Now, for local maxima and minima,
Put f'(x) =0
cos x = -sin x
tan x = -1
x = 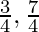 ∈ (0, 2π)
∈ (0, 2π)
Now again differentiate the given function w.r.t. x
f”(x) = -sin x + cos x
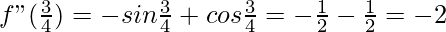 <0
<0
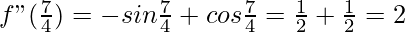 >0
>0
Therefore, by second derivative test, 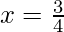 is a point of local maxima
is a point of local maxima
Hence, the maximum value is 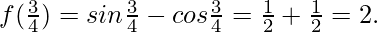
However, 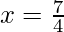 is a point of local minima
is a point of local minima
Hence, the minimum value is 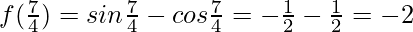
问题9. f(x)= cos x,0
解决方案:
Given function
f(x) = cos x, 0< x < π
Now, differentiate the given function w.r.t. x
f'(x) = – sin x
Now, for local maxima and minima,
Put f ‘(x) – 0
⇒ – sin x = 0
⇒ x = 0, and π
But, these two points lies outside the interval (0, π)
So, no local maxima and minima will exist in the interval (0, π).
问题10。f(x)= sin 2x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = sin2x – x
Now, differentiate the given function w.r.t. x
f ‘(x) = 2 cos 2x – 1
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 2cos 2x – 1 = 0
⇒ cos 2x = 1/2 = cos π/3
⇒ 2x = π/3, -π/3
⇒ x = 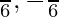
At x = -π/6, f'(x) changes from negative to positive. Hence, x = π/6 is point of local minima.
So, the minimum value is 
At x = π/6, f'(x) changes from positive to negative. Hence, x = π/6 is point of local maxima
The maximum value is 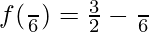
问题11. f(x)= 2sin x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = 2sin x – x, -π/2≤ x ≤ π/2
Now, differentiate the given function w.r.t. x
f ‘(x) = 2cos x – 1 = 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ cos x = 1/2 = cos π/3
⇒ x = -π/3, π/3
So, at x = -π/3, f'(x) changes from negative to positive. Hence, x = -π/3 is point of local minima
So, the minimum value is f(-π/3) = 2sin(-π/3) – (-π/3) = -√3 – π/3
At x = π/3, f'(x) changes from positive to negative. Hence, x = π/3 is point of local minima
The maximum value is f(π/3) = 2sin(π/3) – (π/3) = √3 – π/3
问题12. f(x)= x 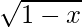 ,x> 0
,x> 0
解决方案:
Given function
f(x) = x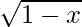 , x > 0
, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 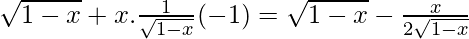
= 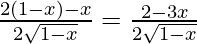
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 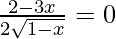
⇒ 2 – 3x = 0
⇒ x = 2/3
f “(x) = ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3x)(\frac{-1}{2\sqrt{1-x}})}{1-x}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2018%20Maxima%20and%20Minima%20%E2%80%93%20Exercise%2018.2_17.jpg)
=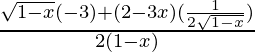
= 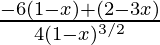
= (3x – 4)/4(1 – x)2
f “(2/3) = 
= 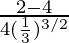
= 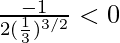
Therefore, x = 2/3 is a point of local maxima and the local maximum value of f at x = 2/3 is
f(2/3) = 2/3(√1/3) = (2√3)/9
问题13. f(x)= x 3 (2x – 1) 3
解决方案:
Given function
f(x) = x3(2x – 1)3
Now, differentiate the given function w.r.t. x
f'(x) = 3x2(2x – 1)2 + 6x3(2x – 1)2
= 3x2(2x – 1)2(2x – 1 + 2x)
= 3x2(4x – 1)
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 3x2(4x – 1) = 0
⇒ x = 0, 1/4
At x = 1/4, f'(x) changes from negative to positive. Hence, x = 1/4 is the point of local minima,
So, the minimum value is f(1/4)= (1/4)3(2(1/4) – 1)3= -1/512
问题14. f(x)= x / 2 + 2 / x,x> 0
解决方案:
Given function
f(x) = x/2 + 2/x, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 1/2 – 2/x2, x > 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 1/2 – 2/x2 = 0
⇒ x2 – 4 = 0
⇒ x = 2, -2
At x = 2, f'(x) changes from negative to positive. Hence, x = 2 is point of local minima
So, the local minimum value is f(2) = 2/2 + 2/2 = 2
问题15. f(x)= 1 /(x 2 + 2)
解决方案:
Given function
f(x) = 1/(x2 + 2)
Now, differentiate the given function w.r.t. x
f'(x) = -(2x)/(x2 + 2)2
Now, for local maxima and minima,
Put f'(x) = 0 f'(x) = 0
f'(x) = -(2x)/(x2 + 2)2 = 0
⇒ x = 0
At x = 0–, f'(x) > 0
At x = 0+, f'(x) < 0
Therefore, local minimum and maximum value of f(0) = 1/2
解决方案:
Given function
f(x) = sin2x, 0 < x, π
Now, differentiate the given function w.r.t. x
f'(x) = 2 cos 2x
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 2x = ![]()
⇒ x = ![]()
At x = π/4, f'(x) changes from positive to negative. Hence, x = π/4, Is point of local maxima
So, the maximum value is f(π/4) = sin2(π/4) = 1
At x = 3π/4, f'(x) changes from negative to positive. Hence, x = 3π/4 is point of local minima,
So, the minimum value is f(3π/4) = sin2(3π/4) = -1
问题8. f(x)= sin x – cos x,0
解决方案:
Given function
f(x) = sin x – cos x, 0 < x < 2π
Now, differentiate the given function w.r.t. x
f'(x)= cos x + sin x
Now, for local maxima and minima,
Put f'(x) =0
cos x = -sin x
tan x = -1
x = 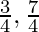 ∈ (0, 2π)
∈ (0, 2π)
Now again differentiate the given function w.r.t. x
f”(x) = -sin x + cos x
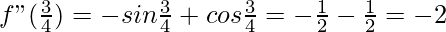 <0
<0
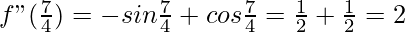 >0
>0
Therefore, by second derivative test, 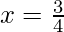 is a point of local maxima
is a point of local maxima
Hence, the maximum value is 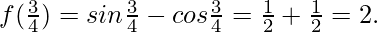
However, 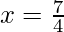 is a point of local minima
is a point of local minima
Hence, the minimum value is 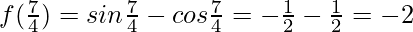
问题9. f(x)= cos x,0
解决方案:
Given function
f(x) = cos x, 0< x < π
Now, differentiate the given function w.r.t. x
f'(x) = – sin x
Now, for local maxima and minima,
Put f ‘(x) – 0
⇒ – sin x = 0
⇒ x = 0, and π
But, these two points lies outside the interval (0, π)
So, no local maxima and minima will exist in the interval (0, π).
问题10。f(x)= sin 2x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = sin2x – x
Now, differentiate the given function w.r.t. x
f ‘(x) = 2 cos 2x – 1
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 2cos 2x – 1 = 0
⇒ cos 2x = 1/2 = cos π/3
⇒ 2x = π/3, -π/3
⇒ x = 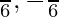
At x = -π/6, f'(x) changes from negative to positive. Hence, x = π/6 is point of local minima.
So, the minimum value is 
At x = π/6, f'(x) changes from positive to negative. Hence, x = π/6 is point of local maxima
The maximum value is 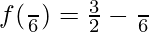
问题11. f(x)= 2sin x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = 2sin x – x, -π/2≤ x ≤ π/2
Now, differentiate the given function w.r.t. x
f ‘(x) = 2cos x – 1 = 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ cos x = 1/2 = cos π/3
⇒ x = -π/3, π/3
So, at x = -π/3, f'(x) changes from negative to positive. Hence, x = -π/3 is point of local minima
So, the minimum value is f(-π/3) = 2sin(-π/3) – (-π/3) = -√3 – π/3
At x = π/3, f'(x) changes from positive to negative. Hence, x = π/3 is point of local minima
The maximum value is f(π/3) = 2sin(π/3) – (π/3) = √3 – π/3
问题12. f(x)= x 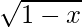 ,x> 0
,x> 0
解决方案:
Given function
f(x) = x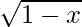 , x > 0
, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 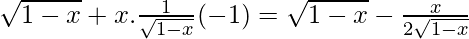
= 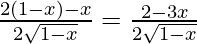
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 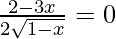
⇒ 2 – 3x = 0
⇒ x = 2/3
f “(x) = ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3x)(\frac{-1}{2\sqrt{1-x}})}{1-x}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2018%20Maxima%20and%20Minima%20%E2%80%93%20Exercise%2018.2_17.jpg)
=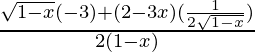
= 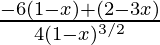
= (3x – 4)/4(1 – x)2
f “(2/3) = 
= 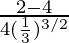
= 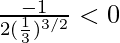
Therefore, x = 2/3 is a point of local maxima and the local maximum value of f at x = 2/3 is
f(2/3) = 2/3(√1/3) = (2√3)/9
问题13. f(x)= x 3 (2x – 1) 3
解决方案:
Given function
f(x) = x3(2x – 1)3
Now, differentiate the given function w.r.t. x
f'(x) = 3x2(2x – 1)2 + 6x3(2x – 1)2
= 3x2(2x – 1)2(2x – 1 + 2x)
= 3x2(4x – 1)
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 3x2(4x – 1) = 0
⇒ x = 0, 1/4
At x = 1/4, f'(x) changes from negative to positive. Hence, x = 1/4 is the point of local minima,
So, the minimum value is f(1/4)= (1/4)3(2(1/4) – 1)3= -1/512
问题14. f(x)= x / 2 + 2 / x,x> 0
解决方案:
Given function
f(x) = x/2 + 2/x, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 1/2 – 2/x2, x > 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 1/2 – 2/x2 = 0
⇒ x2 – 4 = 0
⇒ x = 2, -2
At x = 2, f'(x) changes from negative to positive. Hence, x = 2 is point of local minima
So, the local minimum value is f(2) = 2/2 + 2/2 = 2
问题15. f(x)= 1 /(x 2 + 2)
解决方案:
Given function
f(x) = 1/(x2 + 2)
Now, differentiate the given function w.r.t. x
f'(x) = -(2x)/(x2 + 2)2
Now, for local maxima and minima,
Put f'(x) = 0 f'(x) = 0
f'(x) = -(2x)/(x2 + 2)2 = 0
⇒ x = 0
At x = 0–, f'(x) > 0
At x = 0+, f'(x) < 0
Therefore, local minimum and maximum value of f(0) = 1/2
解决方案:
Given function
f(x) = sin x – cos x, 0 < x < 2π
Now, differentiate the given function w.r.t. x
f'(x)= cos x + sin x
Now, for local maxima and minima,
Put f'(x) =0
cos x = -sin x
tan x = -1
x = ![]() ∈ (0, 2π)
∈ (0, 2π)
Now again differentiate the given function w.r.t. x
f”(x) = -sin x + cos x
![]() <0
<0
![]() >0
>0
Therefore, by second derivative test, ![]() is a point of local maxima
is a point of local maxima
Hence, the maximum value is ![]()
However, ![]() is a point of local minima
is a point of local minima
Hence, the minimum value is ![]()
问题9. f(x)= cos x,0
解决方案:
Given function
f(x) = cos x, 0< x < π
Now, differentiate the given function w.r.t. x
f'(x) = – sin x
Now, for local maxima and minima,
Put f ‘(x) – 0
⇒ – sin x = 0
⇒ x = 0, and π
But, these two points lies outside the interval (0, π)
So, no local maxima and minima will exist in the interval (0, π).
问题10。f(x)= sin 2x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = sin2x – x
Now, differentiate the given function w.r.t. x
f ‘(x) = 2 cos 2x – 1
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 2cos 2x – 1 = 0
⇒ cos 2x = 1/2 = cos π/3
⇒ 2x = π/3, -π/3
⇒ x = 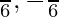
At x = -π/6, f'(x) changes from negative to positive. Hence, x = π/6 is point of local minima.
So, the minimum value is 
At x = π/6, f'(x) changes from positive to negative. Hence, x = π/6 is point of local maxima
The maximum value is 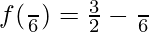
问题11. f(x)= 2sin x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = 2sin x – x, -π/2≤ x ≤ π/2
Now, differentiate the given function w.r.t. x
f ‘(x) = 2cos x – 1 = 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ cos x = 1/2 = cos π/3
⇒ x = -π/3, π/3
So, at x = -π/3, f'(x) changes from negative to positive. Hence, x = -π/3 is point of local minima
So, the minimum value is f(-π/3) = 2sin(-π/3) – (-π/3) = -√3 – π/3
At x = π/3, f'(x) changes from positive to negative. Hence, x = π/3 is point of local minima
The maximum value is f(π/3) = 2sin(π/3) – (π/3) = √3 – π/3
问题12. f(x)= x 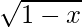 ,x> 0
,x> 0
解决方案:
Given function
f(x) = x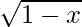 , x > 0
, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 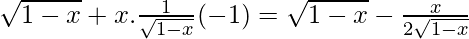
= 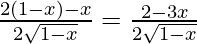
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 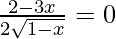
⇒ 2 – 3x = 0
⇒ x = 2/3
f “(x) = ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{\sqrt{1-x}(-3)-(2-3x)(\frac{-1}{2\sqrt{1-x}})}{1-x}]](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2012%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2018%20Maxima%20and%20Minima%20%E2%80%93%20Exercise%2018.2_17.jpg)
=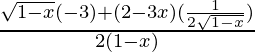
= 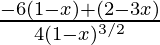
= (3x – 4)/4(1 – x)2
f “(2/3) = 
= 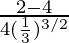
= 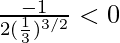
Therefore, x = 2/3 is a point of local maxima and the local maximum value of f at x = 2/3 is
f(2/3) = 2/3(√1/3) = (2√3)/9
问题13. f(x)= x 3 (2x – 1) 3
解决方案:
Given function
f(x) = x3(2x – 1)3
Now, differentiate the given function w.r.t. x
f'(x) = 3x2(2x – 1)2 + 6x3(2x – 1)2
= 3x2(2x – 1)2(2x – 1 + 2x)
= 3x2(4x – 1)
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 3x2(4x – 1) = 0
⇒ x = 0, 1/4
At x = 1/4, f'(x) changes from negative to positive. Hence, x = 1/4 is the point of local minima,
So, the minimum value is f(1/4)= (1/4)3(2(1/4) – 1)3= -1/512
问题14. f(x)= x / 2 + 2 / x,x> 0
解决方案:
Given function
f(x) = x/2 + 2/x, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 1/2 – 2/x2, x > 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 1/2 – 2/x2 = 0
⇒ x2 – 4 = 0
⇒ x = 2, -2
At x = 2, f'(x) changes from negative to positive. Hence, x = 2 is point of local minima
So, the local minimum value is f(2) = 2/2 + 2/2 = 2
问题15. f(x)= 1 /(x 2 + 2)
解决方案:
Given function
f(x) = 1/(x2 + 2)
Now, differentiate the given function w.r.t. x
f'(x) = -(2x)/(x2 + 2)2
Now, for local maxima and minima,
Put f'(x) = 0 f'(x) = 0
f'(x) = -(2x)/(x2 + 2)2 = 0
⇒ x = 0
At x = 0–, f'(x) > 0
At x = 0+, f'(x) < 0
Therefore, local minimum and maximum value of f(0) = 1/2
解决方案:
Given function
f(x) = cos x, 0< x < π
Now, differentiate the given function w.r.t. x
f'(x) = – sin x
Now, for local maxima and minima,
Put f ‘(x) – 0
⇒ – sin x = 0
⇒ x = 0, and π
But, these two points lies outside the interval (0, π)
So, no local maxima and minima will exist in the interval (0, π).
问题10。f(x)= sin 2x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = sin2x – x
Now, differentiate the given function w.r.t. x
f ‘(x) = 2 cos 2x – 1
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 2cos 2x – 1 = 0
⇒ cos 2x = 1/2 = cos π/3
⇒ 2x = π/3, -π/3
⇒ x = ![]()
At x = -π/6, f'(x) changes from negative to positive. Hence, x = π/6 is point of local minima.
So, the minimum value is ![]()
At x = π/6, f'(x) changes from positive to negative. Hence, x = π/6 is point of local maxima
The maximum value is ![]()
问题11. f(x)= 2sin x – x,-π/ 2≤x≤π/ 2
解决方案:
Given function
f(x) = 2sin x – x, -π/2≤ x ≤ π/2
Now, differentiate the given function w.r.t. x
f ‘(x) = 2cos x – 1 = 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ cos x = 1/2 = cos π/3
⇒ x = -π/3, π/3
So, at x = -π/3, f'(x) changes from negative to positive. Hence, x = -π/3 is point of local minima
So, the minimum value is f(-π/3) = 2sin(-π/3) – (-π/3) = -√3 – π/3
At x = π/3, f'(x) changes from positive to negative. Hence, x = π/3 is point of local minima
The maximum value is f(π/3) = 2sin(π/3) – (π/3) = √3 – π/3
问题12. f(x)= x 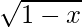 ,x> 0
,x> 0
解决方案:
Given function
f(x) = x![]() , x > 0
, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = ![]()
= ![]()
Now, for local maxima and minima,
Put f'(x) = 0
⇒ ![]()
⇒ 2 – 3x = 0
⇒ x = 2/3
f “(x) = ![]()
=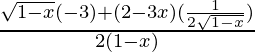
= ![]()
= (3x – 4)/4(1 – x)2
f “(2/3) = 
= ![]()
= ![]()
Therefore, x = 2/3 is a point of local maxima and the local maximum value of f at x = 2/3 is
f(2/3) = 2/3(√1/3) = (2√3)/9
问题13. f(x)= x 3 (2x – 1) 3
解决方案:
Given function
f(x) = x3(2x – 1)3
Now, differentiate the given function w.r.t. x
f'(x) = 3x2(2x – 1)2 + 6x3(2x – 1)2
= 3x2(2x – 1)2(2x – 1 + 2x)
= 3x2(4x – 1)
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 3x2(4x – 1) = 0
⇒ x = 0, 1/4
At x = 1/4, f'(x) changes from negative to positive. Hence, x = 1/4 is the point of local minima,
So, the minimum value is f(1/4)= (1/4)3(2(1/4) – 1)3= -1/512
问题14. f(x)= x / 2 + 2 / x,x> 0
解决方案:
Given function
f(x) = x/2 + 2/x, x > 0
Now, differentiate the given function w.r.t. x
f'(x) = 1/2 – 2/x2, x > 0
Now, for local maxima and minima,
Put f'(x) = 0
⇒ 1/2 – 2/x2 = 0
⇒ x2 – 4 = 0
⇒ x = 2, -2
At x = 2, f'(x) changes from negative to positive. Hence, x = 2 is point of local minima
So, the local minimum value is f(2) = 2/2 + 2/2 = 2
问题15. f(x)= 1 /(x 2 + 2)
解决方案:
Given function
f(x) = 1/(x2 + 2)
Now, differentiate the given function w.r.t. x
f'(x) = -(2x)/(x2 + 2)2
Now, for local maxima and minima,
Put f'(x) = 0 f'(x) = 0
f'(x) = -(2x)/(x2 + 2)2 = 0
⇒ x = 0
At x = 0–, f'(x) > 0
At x = 0+, f'(x) < 0
Therefore, local minimum and maximum value of f(0) = 1/2