圆内刻形状–解决问题

在几何，有特定的分类，其中的形状的其他形状内发现的，例如，三角形内的圆，圆内四边形等形状被称为内接与外接。内部形状称为“内切形状”，而外部形状称为“外切形状”。假设圆以任何其他形状(多边形)内切，则多边形的边缘(全部与圆接触)是圆的切线。

刻在一个圆上的直角三角形

如果将三角形插入到一个圆中，使得该三角形的边之一为圆的直径，则该三角形为直角三角形。

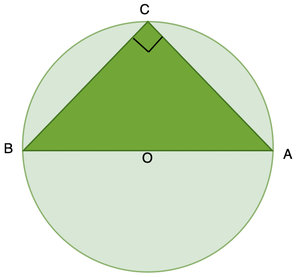
这也称为Thales定理。

证明：

The below diagram has the OC line segment added to it. 

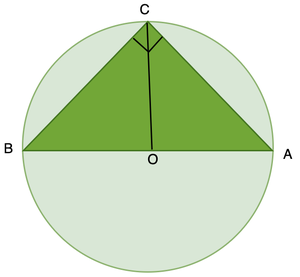
Since segments OB, OC, and OA are all radii of the same circle, they are all congruent. Therefore, both triangles COB and COA are isosceles triangles. Angles B and BCO are congruent since they are opposite congruent sides of the isosceles triangle COB. Similarly, angles A and ACO are congruent because they are opposite congruent sides of the triangle COA.

The sum of the measures of the three angles in a triangle is 180 degrees and so,

m(∠A) + m(∠B) + m(∠C) = 180

Using the angle equivalences from the previous paragraph

m(∠C) = m(∠BCO) + m(∠ACO)

           = m(∠CBO) + m(∠CAO)

= m(∠B) + m(∠A)

Substituting this into the previous formula we find

2m(∠A) + 2m(∠B) = 180

and so m(∠A) + m(∠B) = 90. Since the measures of the three angles of triangle ABC add to 180 this means that m(∠C) = 90° and so triangle ABC is a right triangle as desired.

问题：三角形ΔABC刻在圆O中，侧面AC穿过圆的中心。找到圆的直径。

回答：

 We know that the triangle inscribed by a chord that passes through the centre of the circle is a right triangle. 

Given, BC = 16 and AB = 12. 

Hypotenuse theorem can be applied here, 

$AC^{2}= AB^{2} + BC^{2} \\ = AC^{2} = 12^2 + 16^2 \\ = AC = \sqrt{12^2 + 16^2} \\ = AC = \sqrt{144 + 256}\\ = AC = \sqrt{400} \\ = AC = 20$

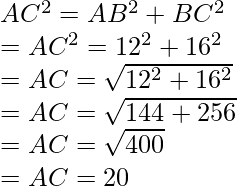
The diameter of the circle is 20. 

内切圆角

定义圆中的内切角的方式是使其两个侧面/光线充当圆的弦，并且该角度的顶点位于圆的圆周上。

当添加另一个顶点位于其中心的角度并且光线与前一个角度的末端相交时，该中心角度所对向的角度将变为该角度所对向的角度的两倍。

循环四边形

当四边形被刻在圆上时，四边形的所有顶点都将接触圆的圆周。循环四边形具有某些属性。

属性：循环四边形的对角始终相加为180°。或可以说，自然界中对角是互补的。

∠A+∠C= 180°

∠B +∠D = 180°

加上所有角度后，, A +∠B+∠C+∠D= 180 + 180 = 360°

问题1：在下图中，找到另一个角度。

回答：

Since both the angles inscribed are from the same arc, the angles must be equal. 

So, the other angle is also 75^o

问题2：在下图中，找到次电弧AC的长度。

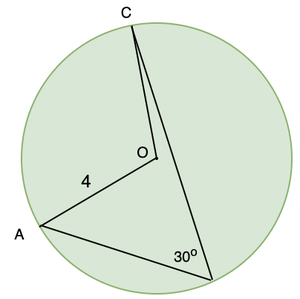
回答：

 By the theorem studied earlier, we know that the angle inscribed on the circle by an arc is half of the angle inscribed at the centre by that same arc. Therefore, ∠AOC = 60°. 

Now we have the angle inscribed at the centre and the radius of the circle is 4cm(given). 

The length of the arc can be found out by

 $angle\text{ (in radians)} = \frac{arc}{radius} \\ arc = angle \times radius \\$

30° is given as $\frac{\pi}{6}$ in radian. 

So, plugging the values in the above formula. 

$arc = \frac{\pi}{6} \times 4 \\ = \frac{4\pi}{6}\\ = \frac{4 \times 3.14}{6}\\ = \frac{12.56}{6} \\ = 2.0943$

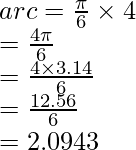
So, the length of the arc is 2.0943. 

问题3：在给定的图中，CD是等于圆半径的弦，AB是如图所示的直径，弦AC和BD延伸到圆之外以在E处相遇。证明∠AEB= 60°

回答：

To Prove: ∠AEB = 60°

Construction: Join OC, OD and BC with dotted lines.

Proof: △COD is an equilateral triangle since all three sides are equal to the radius of the circle.

So, ∠COD= 60° and ∠CBD = 30° (half of the angle subtended at the centre)

In △ACB, ∠ACB = 90°

∠BCE= 180-90 (as AE is a straight line) = 90°

In △BCE, ∠BEC + 90+ 30 = 180°

∠BEC = 60°

Therefore, ∠AEB = 60°