以下是位姿[{a,b,c,d,e},≤]的Hasse图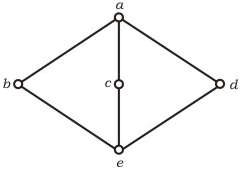
姿势是
(一)不是晶格
(B)晶格但不是分布晶格
(C)分布格但不是布尔代数
(D)布尔代数答案: (B)
解释:
It is a lattice but not a distributive lattice.
Table for Join Operation of above Hesse diagram
V |a b c d e
________________
a |a a a a a
b |a b a a b
c |a a c a c
d |a a a d d
e |a b c d e
Table for Meet Operation of above Hesse diagram
^ |a b c d e
_______________
a |a b c d e
b |b b e e e
c |c e c e e
d |d e e d e
e |e e e e e
Therefore for any two element p, q in the lattice (A,<=)
p <= p V q ; p^q <= p
This satisfies for all element (a,b,c,d,e).
which has 'a' as unique least upper bound and 'e' as unique
greatest lower bound.
The given lattice doesn't obey distributive law, so it is
not distributive lattice,
Note that for b,c,d we have distributive law
b^(cVd) = (b^c) V (b^d). From the diagram / tables given above
we can verify as follows,
(i) L.H.S. = b ^ (c V d) = b ^ a = b
(ii) R.H.S. = (b^c) V (b^d) = e v e = e
b != e which contradict the distributive law.
Hence it is not distributive lattice.
so, option (B) is correct. 这个问题的测验