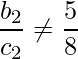代数方程组的解数

一个或多个变量的两个数学表达式相同的说法称为方程。线性方程是所有相关变量的幂均相等的方程。线性方程的次数始终为1。一对线性方程组的同时求解是一对变量“ x”和“ y”的值，它们满足指定方程组中的所有方程。

对两个变量的线性方程组

可以以ax + by + c = 0的形式放置的方程式，其中两个变量x和y称为线性方程式，其中a，b和c是实数，而a和b都不都是零。 (或在a和b都不为零且a ² + b ² ≠0的情况下应满足此条件)。

e.g.: Consider a pair of linear equations in two variables be 3x + 2y = 6,

Substitute x = 2 and y = 0 in the left-hand side (LHS) as:

⇒ LHS = 3(2) + 2(0) 

           = 6 + 0 

           = 6 = RHS

Therefore, x = 2 and y = 0 is a solution of the equation 2x + 3y = 6.

Now, if x = 1 and y = 1 is substituted in the equation 2x + 3y = 6, then:

LHS = 3(1) + 2(1) 

       = 3 + 2 

       = 5 ≠ RHS

Therefore, x = 1 and y = 1 is not a solution of the equation.

Algebraically, this indicates that the point (2, 0) lies on the line representing the equation 3x + 2y = 6, and the point (1, 1) does not lie on it.

Thus, every solution that satisfies the equation is a point on the line representing it.

像这样的两个线性方程，具有两个变量x和y。这样的方程称为两个变量中的一对线性方程。

代数上，两个变量x和y的线性方程组的一般形式为：

a ₁ x + b ₁ y + c ₁ = 0且

a ₂ x + b ₂ y + c ₂ = 0

其中a ₁ ，b ₁ ，c ₁ ，a ₂ ，b ₂ ，c ₂都是实数( ∈R )，a ₁ ² + b ₁ ² ≠0，a ₂ ² + b ₂ ² ≠0。

两个变量中的线性方程对可能有不同的情况

三种不同类型的线有三种不同的情况：相交线，平行线和重合线，用于确定两个变量中的一对线性方程。

• The lines may intersect each other at a single point. 

As a result, the pair of equations has a unique solution (consistent pair of equations).

e.g.: 2x – 4y = 0 and 6x + 8y – 40 = 0

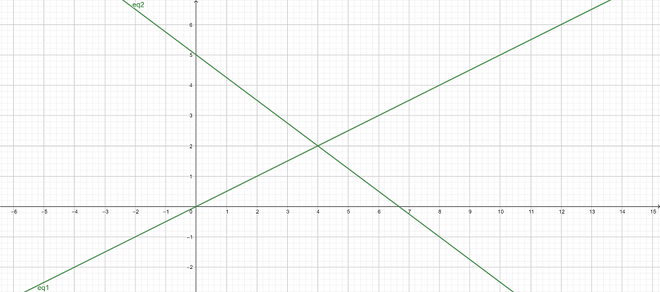
Intersecting lines: 2x – 4y = 0 and 6x + 8y – 40 = 0

• The lines may be parallel to each other. 

As a result, the equations have no solution (inconsistent pair of equations).

e.g.: 2x + 4y – 8 = 0 and 4x + 8y – 24 = 0

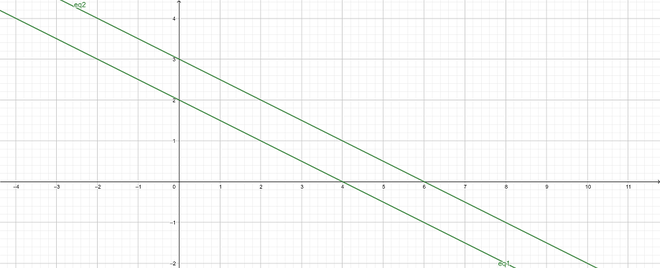
Parallel lines: 2x + 4y – 8 = 0 and 4x + 8y – 24 = 0

• The lines may be coincident. 

As a result, the equations have infinitely many solutions (dependent or consistent pair of equations)

e.g.: 4x + 6y – 18 = 0 and 8x + 12y – 36 = 0

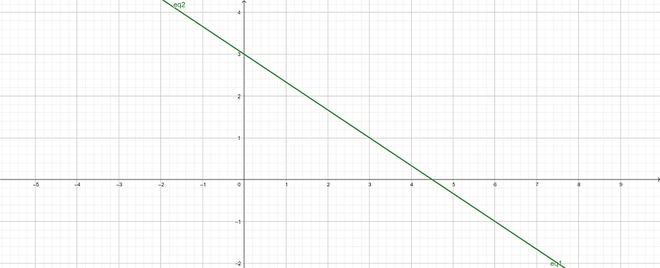
Intersecting lines: 4x + 6y – 18 = 0 and 8x + 12y – 36 = 0

现在，让我们假设这对方程为：a ₁ x + b ₁ y + c ₁ = 0和a ₂ x + b ₂ y + c ₂ = 0现在，它们的对应于比较比率的图形和代数解释为：

Comparing ratios	Graphical  Representation	Algebraic Interpretation
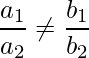$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$	Intersecting  Lines	Exactly one  Solution (unique)
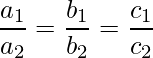$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} = \dfrac{c_1}{c_2}$	Coincident Lines	Infinitely many solutions
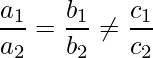$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$	Parallel  Lines	No solution

样本问题

问题1：找出图形表示并指定以下线性方程对的解数：8x – 4y + 10 = 0和4x – 2y + 9 = 0。

解决方案：

For the given pair of linear equations:

a₁ = 8, b₁ = -4, c₁ = 10 and 

a₂ = 4, b₂ = -2, c₂ = 9

Therefore,

a₁ / a₂ = 8 / 4 = 2

b₁ / b₂ = -4 / -2 = 2 and 

c₁ / c₂ = 10 / 9

This implies that:

$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$

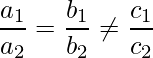
Hence, the given pairs of linear equations have no solution and the lines are parallel and never intersect each other.

问题2：确定以下线性方程对的解数：6x + 2y = 4和7x – 3y = 13。

For the given pair of linear equations:

a₁ = 6, b₁ = 2, c₁ = -4 and 

a₂ = 7, b₂ = -3, c₂ = -13

Therefore,

a₁ / a₂ = 6 / 7 

b₁ / b₂ = 2 / -3 and 

c₁ / c₂ = -4 / -13

This implies that:

$\frac{a_1}{a_2} \neq \frac{b_1}{b_2}$

Hence, the given pairs of linear equations have a unique solution and the lines intersect each other at exactly one point.

问题3：确定以下线性方程对的图形表示形式和解的数量：6x – 5y = 11; – 12x + 10y = –22。

For the given pair of linear equations:

a₁ = 6, b₁ = -5, c₁ = -11 and 

a₂ = -12, b₂ = 10, c₂ = 22

Therefore,

a₁ / a₂ = 6 / -12 = -1 / 2

b₁ / b₂ = -5 / 10 = -1 / 2 and 

c₁ / c₂ = -11 / 22

This implies that:

$\frac{a_1}{a_2} = \frac{b_1}{b_2} = \frac{c_1}{c_2}$

Hence, the given pairs of linear equations have infinite many solutions and the lines are coincident.

问题4：在以下单词问题中制作一对线性方程，并以图形方式找到其解。

一班有20名学生。如果男孩的数量比女孩的数量多6，请在班级中找到男孩和女孩的数量。

解决方案：

Consider, the number of girls be x and the number of boys be y.

Therefore, according to the given conditions:

x + y = 20                                                                                                                     ……(1)

x – y = 6                                                                                                                       ……(2)

In order, to construct the graph the solutions of the given equation is needed to be determined.  

For equation (1): x + y = 20, the solutions are:

x	y
0	20
20	0

For equation (2): x – y = 6, So, the solutions are:

x	y
0	-6
6	0

Thus, plotting the above points for equation (1) and (2) as:

Now, from the graph it can be concluded that the given lines intersect each other at point (13, 7).

Hence, the number of girls are 7 and number of boys are 13 in a class.

问题5：确定两个变量中的其他线性方程，使其形成：

(i)与6x + 7y – 8 = 0的线相交。

(ii)与线4x-5y-8 = 0平行的线。

解决方案：

(i)

In order to make a pair of lines intersect, they must satisfy the given conditions:

$\dfrac{a_1}{a_2} \neq \dfrac{b_1}{b_2}$

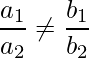
On rearranging the above expression as:

$\frac{a_1}{b_1} \neq \frac{a_2}{b_2}$

Therefore, in the equation the ratio should not be 6/7.

So, another equation can be 5x – 9y + 9 = 0

where the ratio is 5 / -9 and 

$\dfrac{6}{7} \neq \dfrac{5}{-9}$

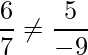
(ii)

In order to make a pair of lines parallel, they should satisfy the given conditions:

$\dfrac{a_1}{a_2} = \dfrac{b_1}{b_2} \neq \dfrac{c_1}{c_2}$

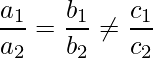
On rearranging the above expression as:

$\dfrac{a_1}{b_1} = \dfrac{a_2}{b_2}$

$\dfrac{b_1}{c_1} \neq \dfrac{b_2}{c_2}$

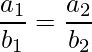
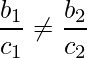
Therefore, the required equation a₂ / b₂ should be in ratio of 4 / -5 and b₂ / c₂ should not be equal to -5 / -8.

So, another equation can be 8x – 10y + 9 = 0

where the ratio a₂ / b₂ is 8/-10 = -8/10 and

$\dfrac{b_2}{c_2} \neq \dfrac{5}{8}$