圆上一点的切线数

圆是平面中距特定点恒定距离的所有点的集合。该距离称为圆的半径，而固定点称为圆心。直线和圆可以三种方式共存，一种可以是与圆的圆周不相交的直线，在圆和直线之间总是存在一定的空间。第二种类型是当线以使其通过并接触圆的圆周的方式放置时，称为圆的切线。第三种是线在两个地方与圆周相交的地方，被称为割线。它们显示如下，

1. 无路口
2. 切线
3. 割线

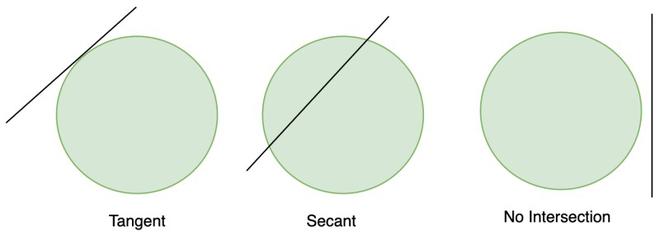
割线在两个点处相交圆，而切线在一个点处相交。让我们详细研究切线及其属性。

切线

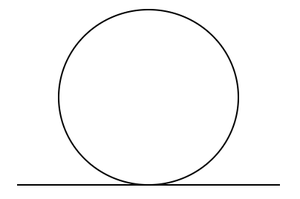
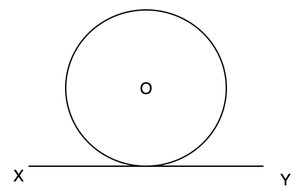
仅在一点处与圆相交的线称为切线。圆具有无限多个可能的切线。切线和圆的公共点称为接触点。

让我们通过定理了解切线的一些属性。

从点到圆的切线数

众所周知，切线定义为通过的线接触圆的圆周。为此，我们需要进行一些实验。通过不同的实验可以得到三种情况。

情况1：从圆内切线

让我们尝试从圆内绘制切线。让我们假设圆内有一个点P并尝试绘制切线。我们观察到不可能从圆内部绘制切线。

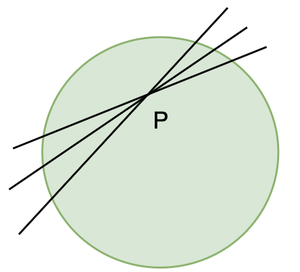
情况2：圆上的一点

我们可以在本文开头的图中看到，我们可以从圆上的任意点绘制切线。实际上，一个圆上可以有无限多个切线。

情况3：圆外的点

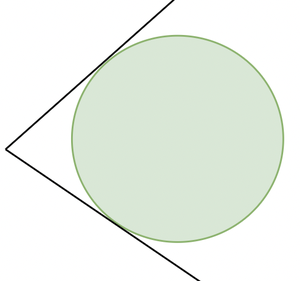
从图中可以看出，从圆外的一点可以绘制两个切线。

因此，总结两种情况：

1. 从圆内的点到圆没有切线。
2. 从圆上的一点到圆的切线。
3. 从圆外的点到圆有两个切线。

切线的性质

定理1：

The tangent at any point of a circle is perpendicular to the radius through the point of contact. 

证明：

Let’s assume a circle with centre O and a tangent XY to circle. 

Let’s assume any point Q on the line XY and join the point of contact with centre. The diagram will look like this, 

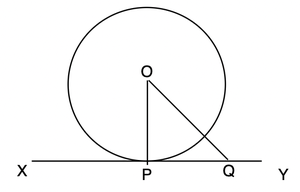
Now the point Q when joined to centre forms OQ, if it is extended it will become a secant not tangent. Now we can see that, 

OQ > OP 

This is true when Q is any point on the line XY except the point of contact (P). P is the point on line XY whose distance is shortest from the centre O. Thus, OP must be perpendicular to XY. 

Hence, Proved. 

该定理还使我们可以得出其他一些性质：

1. 在圆的任何一点处，只能有一个切线。
2. 连接接触点和中心的线垂直于切线。因此，它也称为切线法线。

定理2：

A line drawn through the end of the radius and perpendicular to it is a tangent to the circle. 

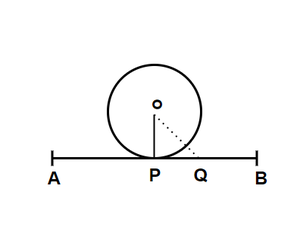
证明：

Let’s assume a circle with centre O in which OP is the radius. A line AB goes through P such OP is perpendicular to AB. 

Now, take a point Q online AB. We know that the distance of Q is shortest from O when Q = P. In every other case,

OQ > OP and Q lies outside the circle. That means AB meets the circle at only one point P. Thus AB is tangent to the circle. 

问题1：在下面的图中。从距离中心41厘米的外部点绘制两个切线。圆的半径为9厘米。找出四边形AOBC的面积。

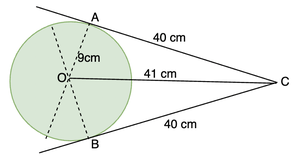
解决方案：

We know from the previous theorem that line joining the centre from point of contact is perpendicular to the tangent. This makes OAC and OBC right-angled triangles. 

So now,

Area of quadrilateral AOBC = Area of triangle AOC + Area of triangle BOC. 

Area of triangle AOC = $\frac{1}{2} \times base \times height = \frac{1}{2} \times 40 \times 9 = 180$ sq units. 

Since both the triangles are congruent, both have the same area. Thus, area of BOC = 180 sq units.

Area of quadrilateral AOBC = 180 + 180 

                                            = 360 sq units. 

问题2：我们假设半径为3cm的圆上的点A处的切线AB。 B点到中心O的距离为5厘米。找出AB的长度。

解决方案：

This is also an application of the theorem studied above, let’s make a diagram first. 

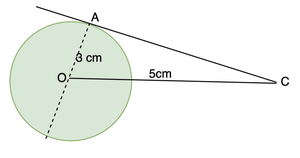
We can see a right-angled triangle AOC here ,

OC² = OA² + AC² 

52 = 32 + AC² 

25 = 9 + AC²

16 = AC²

AC = 4cm 

定理3：

The lengths of tangents drawn from an external point to a circle are equal.

证明：

Let’s assume a circle with centre O, a point C lying outside the circle and the tangents from that point to the circle. AC and BC are the tangents from the point. Our goal is to prove AC = BC.

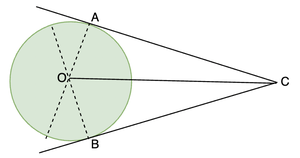
Let’s join OA and OB and consider the two triangles OAC and OBC. 

1. OC is common.
2. ∠OAC = ∠OBC (Right angled triangle)
3. OA = OB (Radii of the circle)

Using RHS property we can say that these two triangles are congruent. Thus, AC = BC. 

定理4：

If two tangents are drawn from an external point then

1. They subtend an equal angle at the centre, and 
2. They are equally inclined to the line segment joining the centre to that point. 

证明：

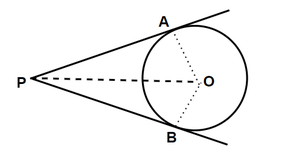
In the given figure, we need to prove that 

∠POA = ∠POB and ∠OPA = ∠OPB.

Let us consider the two triangles, POA and POB. 

PA = PB (By previous theorem) 

OA = OB (radii of the circle) 

OP = OP (Common) 

Thus, these two triangles are congruent. [by SSS] 

Hence, ∠POA = ∠POB and ∠OPA = ∠OPB.

样本问题

问题1：在给定图中，AC和BC是从点C绘制的两个切线。证明2∠OAB= = ACB。

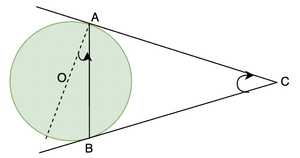
解决方案：

We know from the previous theorem that, AC = BC. This concludes that triangle ABC is an isosceles triangle. 

We also know that ∠OAC = 90°. So, 

∠BAC = 90° – ∠OAB

In triangle BAC

∠BAC + ∠ABC + ∠ACB = 180°

2∠BAC + ∠ACB = 180°

2(90° – ∠OAB) + ∠ACB = 180°

180° – 2∠OAB + ∠ACB = 180°

∠ACB = 2∠OAB 

问题2：在四边形PQRS上刻有一个圆，证明PQ + RS = PS + QR。

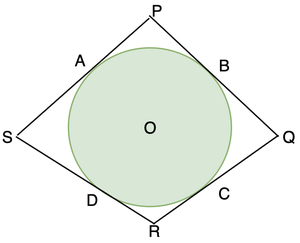
解决方案：

A circle is inscribed inside the quadrilateral PQRS. Notice that the sides of the quadrilateral are actually tangents to the circle. 

PA = PB, 

BQ = QC 

DR = RC 

SA = SD 

We need to prove PQ + RS = PS + QR.

Taking the L.H.S, 

PQ + RS 

⇒ PB + BQ + DR + DS 

⇒ PA + CQ + RC + AS (From the relations stated above)

⇒ (PA + AS) + (CQ + RC) 

⇒ PS + QR 

Hence Proved

问题3：在同心圆中，证明大圆的和弦与小圆的接触在接触点被一分为二。

回答：

Let’s say C₁ and C₂ are two concentric circles. Centre is O and AB is the chord of larger circle. From the previous theorems we know that, OP is perpendicular to AB. As we know from the properties of circle, that perpendicular from the centre bisects the chord. 

AB is chord to larger circle C₁ and OP is perpendicular to it. Thus is bisects the chord.