乘法定理

概率是指事件发生的程度。当发生诸如扔球，从甲板上摘牌等事件时，则该事件一定是与该事件相关联的概率。在数学上，概率是指期望结果与可能结果总数之比。假设第一个事件已发生，则两个事件A和B同时发生的概率等于另一个事件的概率乘积。这称为概率乘法定理。

定理

定理1：如果A和B是与随机实验相关的两个事件，则

如果P(A)≠0，则P(A∩B)= P(A)P(B / A)

或者，如果P(B)≠0，则P(A∩B)= P(B)P(A / B)

证明：

Let S be the sample space associated with the given random experiment. Suppose S contains n elementary events. Let m1,m2 and m be the number of elementary events favorable to A,B and A ∩ B respectively, Then,

P(A) = m₁/n, P(B) = m₂/n and P(A∩B) = m/n

Since m1 elementary events are favorable to A out of which m are favorable to B. Therefore, P(B/A) = m/m₁.                           Similarly, we have P(A/B) = m/m₂.

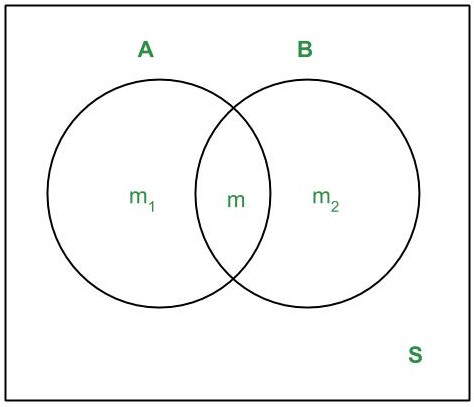
Now,    P(A ∩ B) = m/n

or,        P(A ∩ B) = m/m₁ × m₁/n = P(B/A) × P(A)    … (i)

                                                                                            

Again,  P(A ∩ B) = m/n

or,        P(A ∩ B) = m/m₂ × m₂/n = P(A/B) × P(B)     …(ii)

Note 1:

From (i) and (ii) in the above theorem, we obtain that

P(B/A) = P(A ∩ B)/P(A) and P(A/B) = P(A ∩ B)/P(B)

证明：对于P(B)> 0，P(A / B)≤P(A)

Proof:  

n( A ∩ B) ≤ n(A) and n(B) ≤ n(S)  

Dividing, we get n( A ∩ B) / n(B) ≤ n(A)/ n(S)

                          => P(A/B) ≤ P(A)

Note 2:

(i) The conditional probability P(A/B) is not defined if P(B) = 0.

(ii) P(B / B) = 1

备注：如果A和B是独立事件，则

P(A/B) = P(A) and P(B/A) = P(B)

∴  P(A ∩ B) = P(A) P(B)

定理2：(乘法定理的扩展)。如果A ₁ ，A ₂ ，…，A _n是与随机实验相关的n个事件，则

P(A _{1∩A 2∩…∩A N)=} P(A _{1)P(A 2} / A _{1)P(A 3} / A _{1∩A 2)…×P(A N} / A _{1∩A 2} n…A _n-1 )

其中，P(A _I / A _{1∩A 2∩…∩A I-1)}表示事件A _i的出现的条件概率，考虑到事件A _{1，A 2，…，A I-1}已经发生。

Particular Case: If A, B, C are three events associated with a random experiment, then

P(A ∩ B ∩ C) = P(A) P(B/A) P(C/A ∩ B)

定理3 ：(独立事件的概率乘法定理)如果A和B是两个具有正概率(P(A)≠0，P(B)≠0)的事件，则当且仅当A和B独立

P(A∩B)= P(A)。 P(B)

证明：

We have: P(A ∩ B) = P(A) P(B/A) = P(B) P(A/B); P(A) ≠ 0  . . . (i)

If A and B are independent, i.e A is independent of B and B is independent of A, then, we have 

P(A/B) = P(A) and P(B/A) = P(B) . . . (ii)

From (i) and (ii), we get: P(A ∩ B) = P(A) P(B), as required.

例子

例1：如果在第一次抽签后没有替换抽签的纸牌，请找出从连续洗净的纸包中连续两次抽签中抽出钻石纸牌的概率?

解决方案：

Let A be the event of drawing a diamond card in the first draw and B be the event of drawing a diamond card in the second draw. Then,

P(A) = ₁₃C₁ / ₅₂ C₁ = 13/52 = 1/4

After drawing a diamond card in the first draw 51 cards are left out of which 12 cards are diamond cards.

∴ P(B/A) = Probability of drawing a diamond card in the second draw when a diamond card has already been drawn in the first draw

P(B/A) = ₁₂C₁ / ₅₁C₁ = 12/51 = 4/17

Required probability = P(A ∩ B) = P(A) P(B/A) = 1/4 × 4/17 = 1/17

示例2：一个袋子中包含19张票，编号从1到19。先抽出一张票，然后再抽出另一张无需更换的票。找出两张票证均显示偶数的可能性。

解决方案：

Let A be the event of drawing an even numbered ticket in the first draw and B be the event of drawing an even numbered ticket in the second draw. Then,

Required probability = P(A ∩ B) = P(A) P(B/A)   … (i)

Since there are 19 tickets, numbered 1 to 19, in the bag out of which 9 are even numbered viz. 2, 4, 6, 8, 10, 12, 14, 16, 18.

∴ P(A) = 9/19

Since the ticket drawn in the first draw is not replaced, therefore second ticket drawn is from the remaining 18 tickets, out of which 8 are even numbered.

∴ P(B/A) = 8/18 = 4/9

Substituting these values in (i), we get

Required probability = P(A ∩ B) = P(A) P(B/A) = 9/19 × 4/9 = 4/19

示例3：对40岁的妻子到8岁的丈夫是8：5，而对50岁的丈夫到80岁的丈夫是4：3。

(i)双方都还活着，

(ii)没有人会活着，

(iii)只有妻子会活着，

(iv)只有丈夫会活着

解决方案：

Let us define the events:

A: Wife will be alive, 

B: Husband will be alive 

Then, we are given: 

P(A) = 5/(8 + 5) = 5/13 => P(A’) = 1 – P(A) = 8/13

P(B) = 3/(4 + 3) = 3/7  => P(B’) = 1 – P(B) = 4/7

If we assume that A and B are independent so that A and B’, A’ and B’ are also independent , then the required probabilities are given by:

(i) P(A ∩ B) = P(A)P(B) = (5/13) × (3/7) = 15/91

(ii) P(A’ ∩ B’) = P(A’)P(B’) = (8/13) × (4/7) = 32/91

(iii) P(A ∩ B’) = P(A) – P(A ∩ B) = (5/13) – (15/91) = 20/91

(iv) P(A’ ∩ B) = P(B) – P(A ∩ B) = (3/7) – (15/91) = 24/91