8类RD Sharma解决方案–第3章平方根和平方根–练习3.3 |套装1

问题1.使用列方法找到以下数字的平方。使用常规乘法验证平方。

(i)25

解决方案：

Here, we will break 25 in as between one’s and ten’s position as a = 2 and b = 5. Now,

Step 1: Make 3 columns and write the values of a², 2ab, b² in these columns.

Column 1	Column 2	Column 3
a2	2ab	b2
4	20	25

Step 2: Underline the unit digit of b² and add its ten’s digit(if any) to 2ab.

Column 1	Column 2	Column 3
a2	2ab	b2
4	20 + 2	25
	22

Step 3: Now Underline the unit digit of column 2 and add its ten’s digit(if any) to a²

Column 1	Column 2	Column 3
a2	2ab	b2
4+2	20+2	25
6	22

Step 4: Now underline the number in column 1.

Column 1	Column 2	Column 3
a2	2ab	b2
4+2	20+2	25
6	22

Step 5: Now write the underlined digits respectively as the square.

25² =  625

 Now using multiplication,

25² = 25 x 25 = 625

Because we have the same result in both the methods hence our result is verified.

(ii)37

解决方案：

Here, a = 3, b = 7

Column 1	Column 2	Column 3
a2	2ab	b2
9 + 4	42 + 4	49
13	46

Now write the underlined digits respectively as the square.

37² = 1369

Now using multiplication,

37² = 37 x 37 = 1369

Because we have the same result in both the methods hence our result is verified.

(iii)54

解决方案：

Here, a = 5, b = 4.

Column 1	Column 2	Column 3
a2	2ab	b2
25+4	40+1	16
29	41

Now write the underlined digits respectively as the square.

54² = 2916

Now using multiplication,

54² = 54 x 54 = 2916

Because we have the same result in both the methods hence our result is verified.

(iv)71

解决方案：

Here, a = 7, b = 1.

Column 1	Column 2	Column 3
a2	2ab	b2
49 + 1	14 + 0	1
50	14

Now write the underlined digits respectively as the square.

71² = 5041

Now using multiplication,

71² = 71 x 71 = 5041

Because we have the same result in both the methods hence our result is verified.

(v)96

解决方案：

Here, a = 9, b = 6.

Column 1	Column 2	Column 3
a2	2ab	b2
81 + 11	108 + 3	36
92	113

Now write the underlined digits respectively as the square.

96² = 9216

Now using multiplication,

96² = 96 x 96 = 9216.

Because we have the same result in both the methods hence our result is verified.

问题2.使用对角线法找到以下数字的平方：

(i)98

解决方案：

Because, 98² = 9604

Draw a square table with equal no. of rows and columns as the no. of digits are.

Now divide each block in two parts.

Now, write the digits as depicted, and we have to store the values as provided in each block

Now Store the values as shown and add them as per the subdivision we have made, i.e., 4, 2 + 6 + 2, 7 + 1 + 7, 8 and the previous carry(i.e., take only one unit’s digit and transfer the other as carry).

Now, write the underlined(unit’s digit), as the square of the number

98² = 9604

(ii)273

解决方案：

Because, 273² = 74529

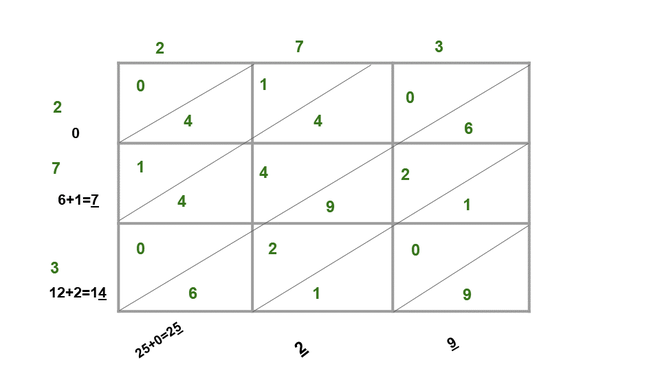
Now, write the underlined(unit’s digit), as the square of the number

273² = 74529

(iii)348

解决方案：

Because, 348² = 121104

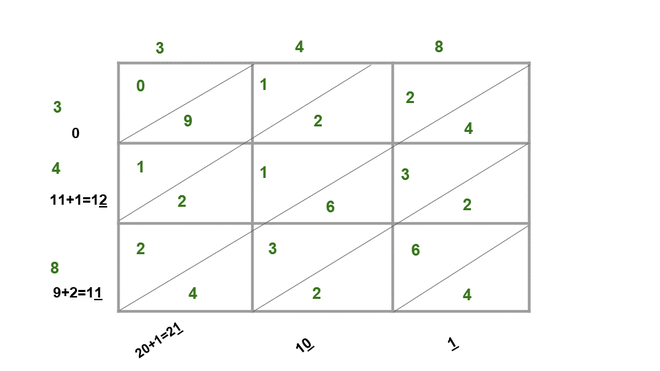
Now, write the unit’s digit as the square of 348,

348² = 121104

(iv)295

解决方案：

Because, 295² = 87025

Now, write each one’s digit as the square of 295,

295² = 87025

(v)171

解决方案：

Because, 171² = 29241

Now, write each one’s digit as the square of 171,

171² = 29241

问题3.找到以下数字的平方：

(i)127

解决方案：

Here let’s take a = 120, b = 7

127² = (120 + 7)² = 120² + (2 x 120 x 7) + 7²

= (120 x 120) + 1680 + (7 x 7)

= 14400 + 1680 + 49

= 16129

Alternatively:

We could also take a = 100, b = 27, 

127² = 10000 + 5400 + 729  = 16129

Thus, 127² = 16129

(ii)503

解决方案：

Here, let’s take a = 500, b = 3.

503² = (500 + 3)² = 500² + (2 x 500 x 3) + 3²

= 250000 + 3000 + 9

= 253009

Alternatively:

503² = 503 x 503 = 253009

Thus, 503² = 253009

(iii)451

解决方案：

Here, let’s take a = 400, b = 51.

451² = (400 + 51)² = 400² + (2 x 400 x 51) + 51²

= 160000 + 40800 + 2601

= 203401

Alternatively:

451² = 451 x 451 = 203401

451² = 203401

(iv)862

解决方案：

Here, let’s take a = 800, b = 62.

862² = (800 + 62)² = 800² + (2 x 800 x 62) + 62²

= 640000 + 99200 + 3844

= 743044

Alternatively:

862² = 862 x 862 = 743044

862² = 743044

(v)265

解决方案：

Here, let’s take a = 200, b = 65.

265² = (200 + 65)² = 200² + (2 x 200 x 65) + 65²

= 40000 + 26000 + 4225

= 70225

Alternatively:

265² = 265 x 265 = 70225

265² = 70225

第3章平方根和根–练习3.3 |套装2