9类RD Sharma解–第13章包含两个变量的线性方程–练习13.3 |套装2

问题11：画出等式2x + 3y = 12的图形。从图形中找到该点的坐标：

(i)y坐标为3。

(ii)其x坐标为-3。

解决方案：

Given:

2x + 3y = 12

We get,

$y=\frac{12-2x}{3}$

Substituting x = 0 in y = $\frac{12-2x}{3}$we get,

$y=\frac{12-2\times0}{3}$

y = 4

Substituting x = 6 in $y= \frac{12-2x}{3}$, we get

$y=\frac{12-2\times6}{3}$

y = 4

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	6
y	4	0

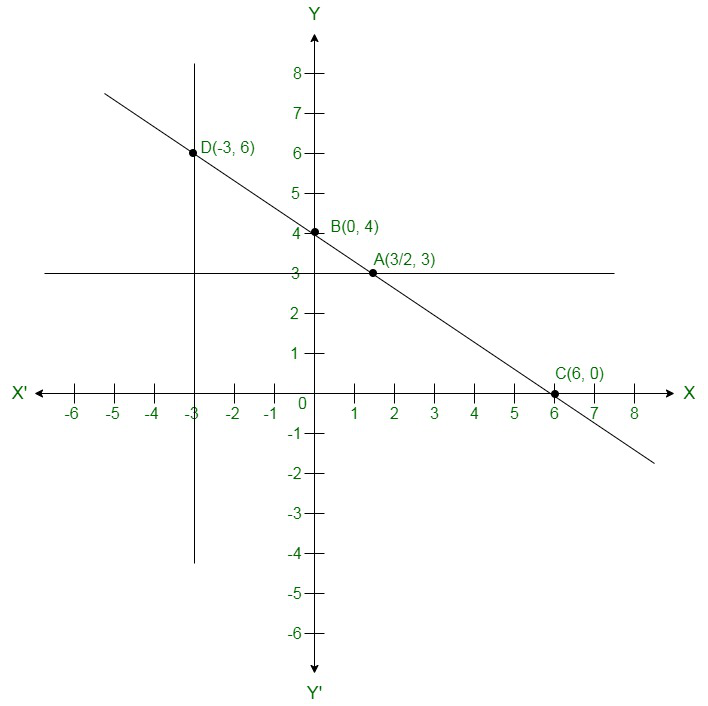
By plotting the given equation on the graph, we get the point B (0, 4) and C (6,0).

(i) Co-ordinates of the point whose y axis is 3 are A $\left(\frac{3}{2},3\right)$

(ii) Co-ordinates of the point whose x -coordinate is –3 are D (-3, 6)

问题12：画出下面给出的每个方程的图。另外，找到图形切割坐标轴的点的坐标：

(i)6x-3y = 12

(ii)-x + 4y = 8

(iii)2x + y = 6

(iv)3x + 2y + 6 = 0

解决方案：

(i) Given:

6x – 3y = 12

We get,

$y=\frac{6x-12}{3}$

Now, substituting x = 0 in $y=\frac{6x-12}{3}$, we get

y = -4

Substituting x = 2 in $y=\frac{6x-12}{3}$, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	2
y	-4	0

Co-ordinates of the points where graph cuts the co-ordinate axes are at y = -4 axis and x = 2  

at x axis.

(ii) Given:

-x + 4y = 8

We get,

$y=\frac{8+x}{4}$

Now, substituting x = 0 in $y=\frac{8+x}{4}$, we get

y = 2

Substituting x = -8 in $y=\frac{8+x}{4}$, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	-8
y	2	0

Co-ordinates of the points where graph cuts the co-ordinate axes are at y = 2 axis and x = -8  

at x axis.

(iii) Given:

2x + y = 6

We get,

y = 6 – 2x

Now, substituting x= 0 in y = 6 – 2x w e get

y = 6

Substituting x = 3 in y = 6 – 2x, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	3
y	6	0

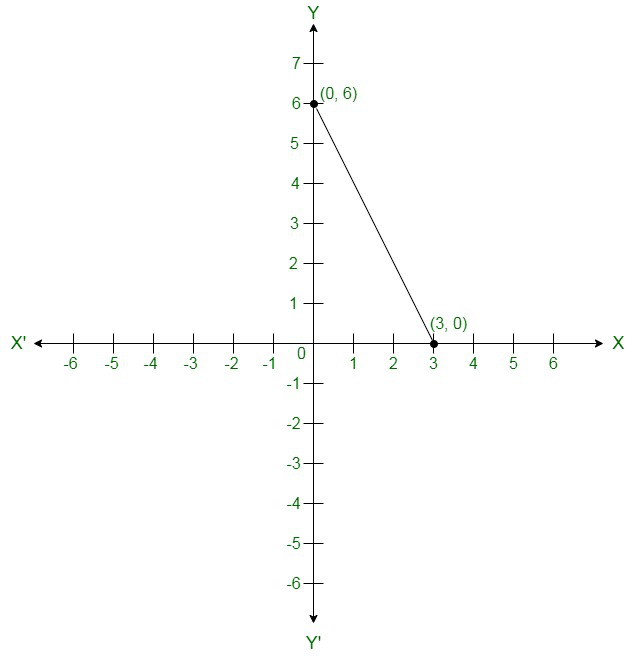
Co-ordinates of the points where graph cuts the co-ordinate axes are y = 6 at y axis and x = 3 

at x axis.

(iv) Given:

3x + 2y + 6 = 0

We get,

$y = \frac{-(6+3x)}{2}$

Now, substituting x = -2 in $y = \frac{-(6+3x)}{2}$, we get

y = -3

Substituting x = -2 in $y = \frac{-(6+3x)}{2}$, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	-2
y	-3	0

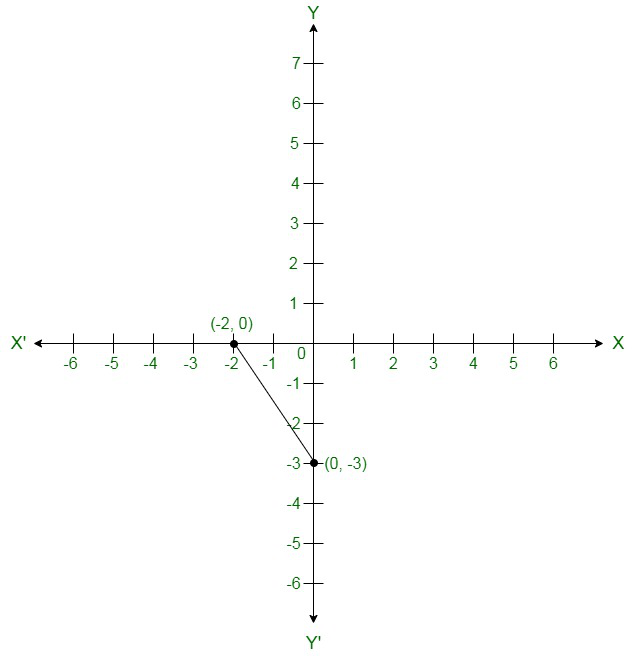
Co-ordinates of the points where graph cuts the co-ordinate axes are y = -3 at y axis and x = -2  

at x axis.

问题13：画出等式2x + y = 6的图形。对图形和坐标轴所包围的区域进行阴影处理。此外，找到阴影区域的面积。

解决方案：

Given:

2x + y = 6

We get,

y = 6 – 2 x

Now, substituting x = 0 in y = 6 – 2x ,we get

y = 6

Substituting x = 3 in y = 6 – 2x ,we get

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	3
y	6	0

The region bounded by the graph is ABC which forms a triangle.

AC at y axis is the base of triangle having AC = 6 units on y axis.

BC at x axis is the height of triangle having BC = 3 units on x axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(6\times3)$

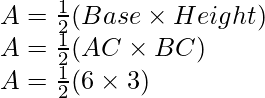
A = 9 sq. units

问题14：画出等式图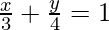$\frac{x}{3}+\frac{y}{4}=1$ 。另外，找到由直线和坐标轴形成的三角形的面积。

解决方案：

Given:

$\frac{x}{3}+\frac{y}{4}=1$

4x + 3y = 12

We get,

$y=\frac{12-4x}{3}$

Now, substituting x = 0 in $y=\frac{12-4x}{3}$, we get

y = 4

Substituting x = 3 in $y=\frac{12-4x}{3}$, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	3
y	4	0

The region bounded by the graph is ABC which form a triangle.

AC at y axis is the base of triangle having AC = 4 units on y axis.

BC at x axis is the height of triangle having BC = 3 units on x axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(4\times3)$

A = 6 sq. units 

问题15：画y = |的图x |。

解决方案：

We are given,

y = |x|

Substituting, x = 1 we get

y = 1

Substituting, x = -1 we get

y = 1

Substituting,x = 2 we get

y = 2

Substituting, x = -2 we get

y = 2

For every value of x, whether positive or negative, we get y as a positive number.

问题16：画y = |的图x | + 2。

解决方案：

Given:

y = |x| + 2

Substituting, x = 0 we get

y = 2

Substituting, x = 1 we get

y = 3

Substituting, x = -1 we get

y = 3

Substituting, x = 2 we get

y = 4

Substituting, x = -2 we get

y = 4

For every value of x, whether positive or negative, we get y as a positive number and the minimum value of y is equal to 2 units.

问题17：在同一座标图纸上画出以下线性方程的图：

2x + 3y = 12，x − y = 1

找出由两条直线形成的三角形的顶点的坐标，以及由这两条直线和x轴界定的区域。

解决方案：

Given:

2x + 3y = 12

We get,

$y=\frac{12-2x}{3}$

Now, substituting x = 0  in $y=\frac{12-2x}{3}$ , we get

y = 4

Substituting x = 6 in $y=\frac{12-2x}{3}$ , we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	6
y	4	0

Plotting A(0,4) and E(6,0) on the graph and by joining the points , we obtain the graph of equation .

Given:

x – y = 1

We get,

y = x − 1

Now, substituting x = 0 in y = x − 1,we get

y = −1

Substituting x = -1  in y = x − 1,we get

y = −2

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	-1
y	-1	-2

Plotting D(0,1) and E(-1,0) on the graph and by joining the points , we obtain the graph of equation .

By the intersection of lines formed by 2x + 3y = 12 and x – y = 1 on the graph, triangle ABC is formed on y axis.

Therefore,

AC at y axis is the base of triangle ABC having AC = 5 units on y axis.

Draw FE perpendicular from F on y axis.

FE parallel to x axis is the height of triangle ABC having FE = 3 units on x axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(5\times3)\\ =\frac{15}{2}sq.\ units$

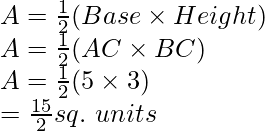
问题18：画出线性方程4x − 3y + 4 = 0和4x + 3y −20 = 0的图。找到由这些线和x轴界定的面积。

解决方案：

Given:

4x – 3y + 4 = 0

We get,

$y=\frac{4x+4}{3}$

Now, substituting x = 0 in $y=\frac{4x+4}{3}$, we get

$y=\frac{4}{3}$

Substituting x = -1 in $y=\frac{4x+4}{3}$, we get

y = 0

Hence, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	-1
y	$\frac{4}{3}$	0

Plotting E(0, $\frac{4}{3}$) and A(-1,0) on the graph and by joining the points, we obtain the graph of equation.

We are given,

4x + 3y – 20 = 0

We get,

$y=\frac{20-4x}{3}$

Now, substituting x = 0 in $y=\frac{20-4x}{3}$, we get

$y=\frac{20}{3}$

Substituting x = 5 in $y=\frac{20-4x}{3}$, we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	5
y	$\frac{20}{3}$	0

Plotting D(0, $\frac{20}{3}$) and B(5,0) on the graph and by joining the points, we obtain the graph of equation.

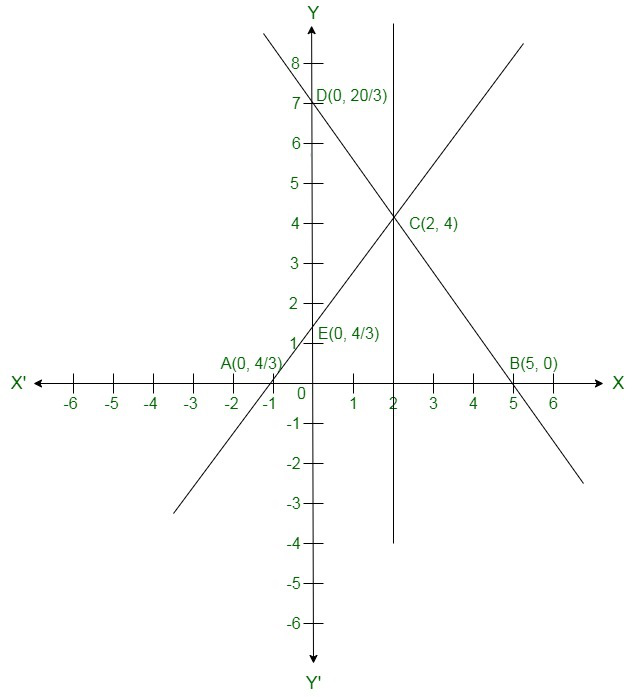
By the intersection of lines formed by 4x – 3y + 4 = 0 and 4x + 3y – 20 = 0 on the graph, triangle ABC is formed on x axis.

Therefore,

AB at x axis is the base of triangle ABC having AB = 6 units on x axis.

Draw CF perpendicular from C on x axis.

CF parallel to y axis is the height of triangle ABC having CF = 4 units on y axis.

Therefore,

Area of triangle ABC, say A is given by

$A=\frac{1}{2}(Base\times Height)\\ A=\frac{1}{2}(AC\times BC)\\ A=\frac{1}{2}(6\times4)\\ A=12sq.\ units$

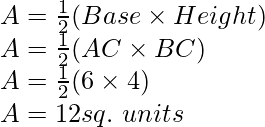
问题19：一列火车A的路径由等式3x + 4y-12 = 0给出，另一列火车B的路径由等式6x + 8y-48 = 0给出。用图形表示这种情况。

解决方案：

Given: Path of train A,

3x + 4y – 12 = 0

We get,

$y=\frac{12-3x}{4}$

Now, substituting x = 0 in $y=\frac{12-3x}{4}$ ,we get

y = 3

Substituting x = 4 in $y=\frac{12-3x}{4}$ ,we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	4
y	3	0

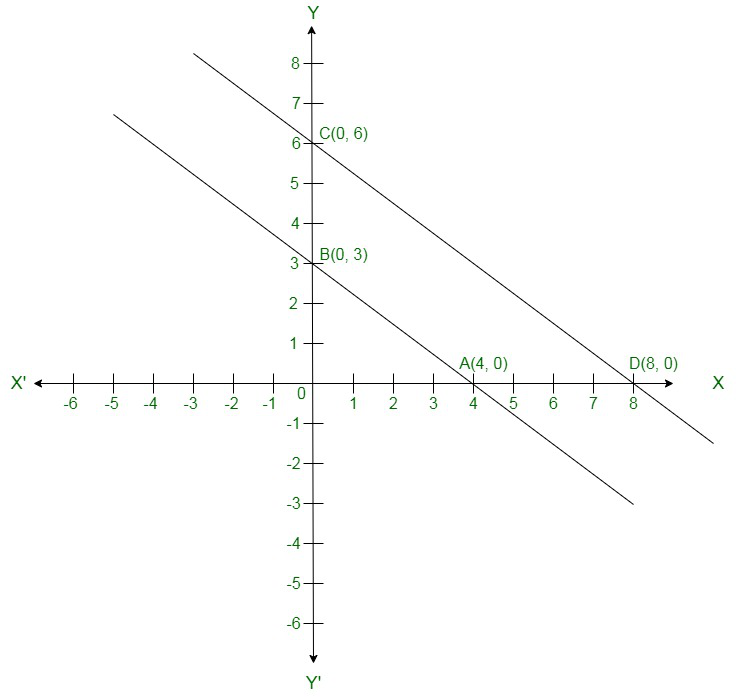
Plotting A(4,0) and E(0,3) on the graph and by joining the points , we obtain the graph of equation .

We are given the path of train B,

6x + 8y – 48 = 0

We get,

$y=\frac{48-6x}{8}$

Now, substituting x = 0 in $y=\frac{48-6x}{8}$,we get

y = 6

Substituting x = 8 in $y=\frac{48-6x}{8}$,we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	8
y	6	0

Plotting C(0,6) and D(8,0) on the graph and by joining the points , we obtain the graph of equation.  

问题20：Ravish告诉他的女儿Aarushi：“七年前，我的年龄是当时的7倍。而且，从现在开始的三年后，我的年龄将是您的三倍。”如果Aarushi和Ravish的当前年龄分别是x和y岁，请用代数和图形方式表示这种情况。

解决方案：

We are given the present age of Ravish as y years and Aarushi as x years.

Age of Ravish seven years ago = y – 7 

Age of Aarushi seven years ago = x – 7

It has already been said by Ravish that seven years ago he was seven times old then Aarushi was then

So,

y – 7 = 7(x – 7)

y – 7 = 7x – 49

7x – y = -7 + 49

7x – y – 42 = 0

Age of Ravish three years from now = y + 3 

Age of Aarushi three years from now = x + 3 

It has already been said by Ravish that three years from now he will be three times old then Aarushi will be then

So,

y + 3 = 3(x + 3)

y + 3 = 3x + 9

3x + 9 – y – 3 = 0

3x – y + 6 = 0

(1) and (2) are the algebraic representation of the given statement.

Given:

7x – y – 42 = 0

We get,

y = 7x – 42

Now, substituting x = 0 in y = 7x – 42 ,we get

y = -42

Substituting x = 6 in y = 7x – 42, we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	6
y	-42	0

Given:

3x – y + 6 = 0

We get,

y = 3x + 6

Now, substituting x = 0 in y = 3x + 6 ,we get

y = 6

Substituting x = -2 in y = 3x + 6 ,we get

y = 0

Therefore, we have the following table exhibiting the abscissa and ordinates of points on the line represented by the given equation

x	0	-2
y	6	0

The red -line represents the equation. 7x – y – 42 = 0

The blue-line represents the equation. 3x – y + 6 = 0

问题21：Aarushi驾驶的汽车匀速为60km / h。绘制距离-时间图。在图表中找到Aarushi在

(一世) $2\frac{1}{2}$小时

(ii) $\frac{1}{2}$小时

解决方案：

Aarushi is driving the car with the uniform speed of 60 km/h.

We represent time on X-axis and distance on Y-axis

Now, graphically

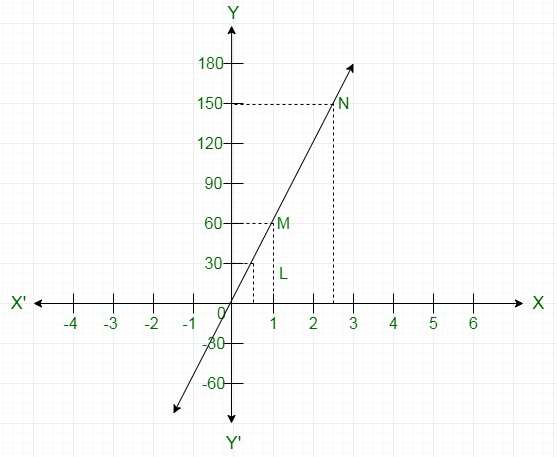
We are given that the car is travelling with a uniform speed 60 km/hr. This means car travels 60 km distance each hour. Thus the graph we get is of a straight line.

Also, we know when the car is at rest, the distance traveled is 0 km, speed is 0 km/hr and the time is also 0 hr.

Therefore, the given straight line will pass through O(0,0) and M(1,60).

Join the points O and M and extend the line in both directions.

Now, we draw a dotted line parallel to y-axis from x = $\frac{1}{2}$ that meets the straight line graph at L from which we draw a line parallel to x-axis that crosses y-axis at 30. Thus, in $\frac{1}{2}$hr, distance traveled by the car is 30 km.

Now, we draw a dotted line parallel to y-axis from x = $2\frac{1}{2}$ that meets the straight line graph at N from which we draw a line parallel to x-axis that crosses y-axis at 150. Thus, in $2\frac{1}{2}$hr, distance traveled by the car is 150 km.

(i) Distance = Speed × Time

Distance traveled in $2\frac{1}{2}$ hours is given by

Distance = $60\times2\frac{1}{2}$

Distance = $60\times\frac{5}{2}$

Distance = 150 km

(ii) Distance = Speed × Time

Distance traveled in $\frac{1}{2}$ hours is given by

Distance = $60\times\frac{1}{2}$

Distance = 30 km