问题1:在两个变量中绘制以下每个线性方程式的图形:
(i)x + y = 4
(ii)x – y = 2
(iii)-x + y = 6
(iv)y = 2x
(v)3x + 5y = 15
(六) ![]()
(vii) ![]()
(viii)2y = -x +1
解决方案:
(i) Given:
x + y = 4
or
y = 4 – x,
Now find values of x and y:
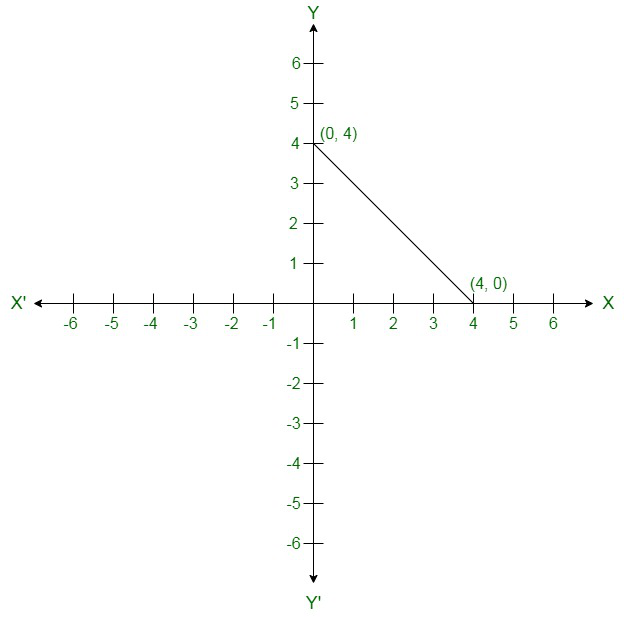
By putting x = 0 ⇒ y = 4
By putting x = 4 ⇒ y = 0
On the Graph: Mark points (0, 4) and (4, 0) on the graph and join them.
(ii) Given:
x – y = 2
Thus,
y = x – 2
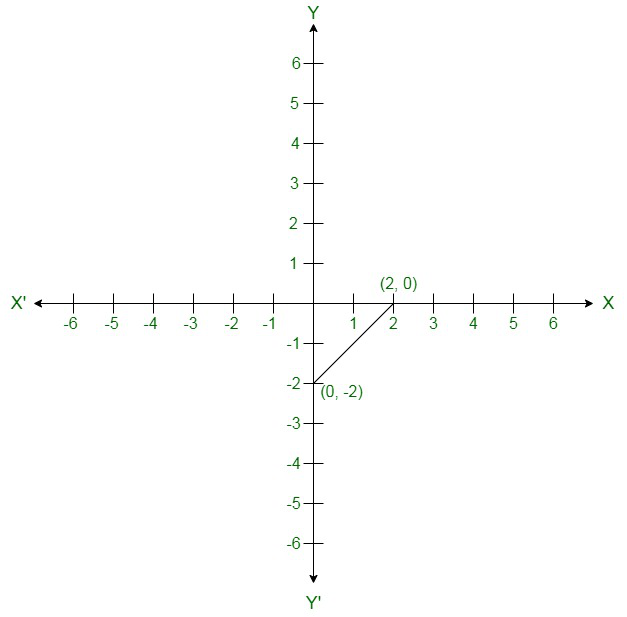
By putting x = 0 ⇒ y = – 2
By putting x = 2 ⇒ y = 0
On the graph: Mark points (0, -2) and (2, 0) on the graph and join them.
(iii) Given:
– x + y = 6
Thus,
y = 6 + x
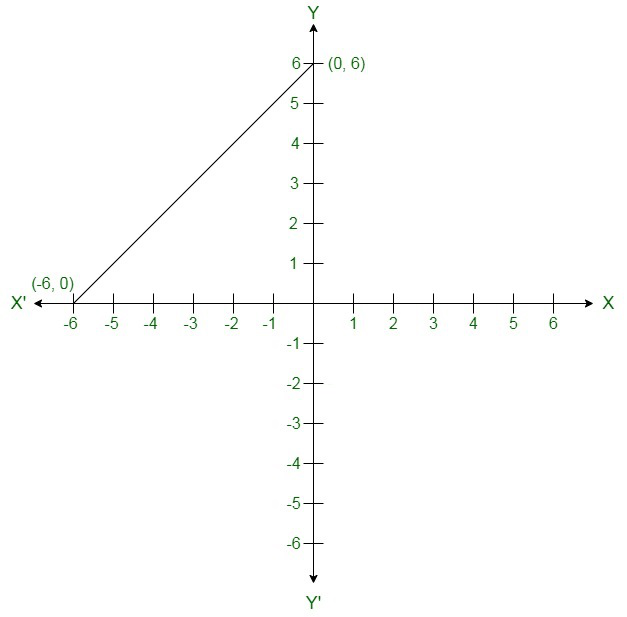
By putting x = 0 ⇒ y = 6
By putting x = -6 ⇒ y = 0
On the graph: Mark points (0, 6) and (-6, 0) on the graph and join them.
(iv) Given:
y = 2x
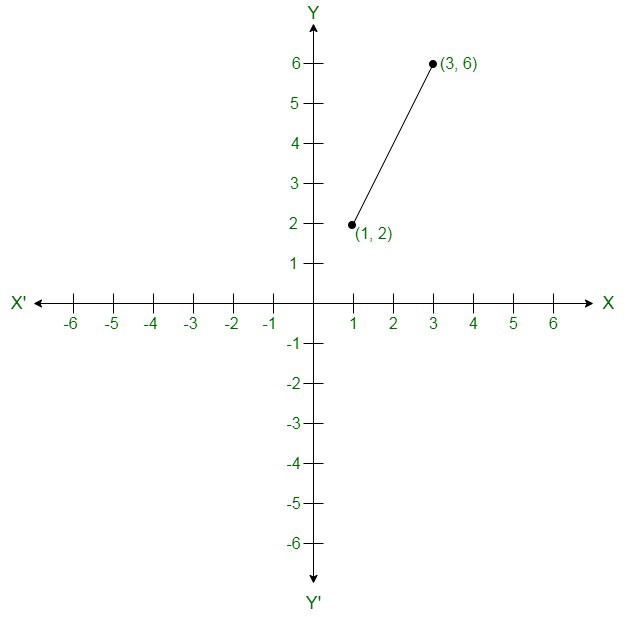
After putting x = 1 ⇒ y = 2
Now put x = 3 ⇒ y = 6
On the graph: Mark points (1, 2) and (3, 6) on the graph and join them.
(v) Given:
3x + 5y = 15
Or
5y = 15 – 3x
By putting x = 0 ⇒ 5y = 15 ⇒ y =3
By putting x = 5 ⇒ 5y = 0 ⇒ y = 0
On the graph: Mark points (0, 3) and (5, 0) on the graph and join them.
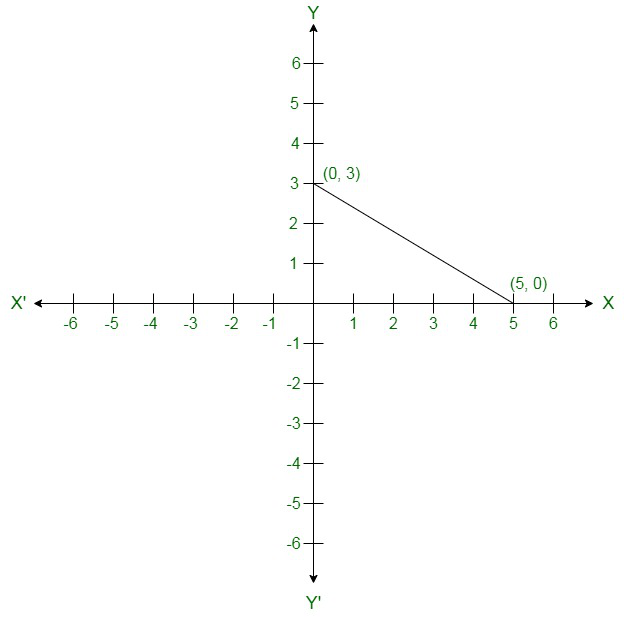
(vi) Given:
![]()
3x – 2y = 12
![]()
By putting x = 0 ⇒ y = -6
By putting x = 4 ⇒ y = 0
On the graph: Mark points (0, -6) and (4, 0) on the graph and join them.
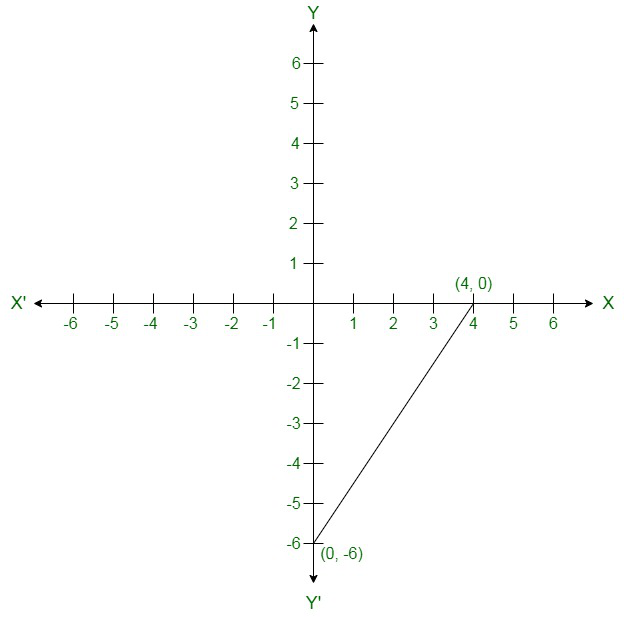
(vii) Given:
![]()
x – 2 = 3(y – 3)
x – 2 = 3y – 9
x = 3y – 7
Now,
By putting x = 5 in x = 3y – 7
y = 4
By putting x = 8 in x = 3y – 7,
y = 5
On the graph: Mark points (5, 4) and (8, 5) on the graph and join them.
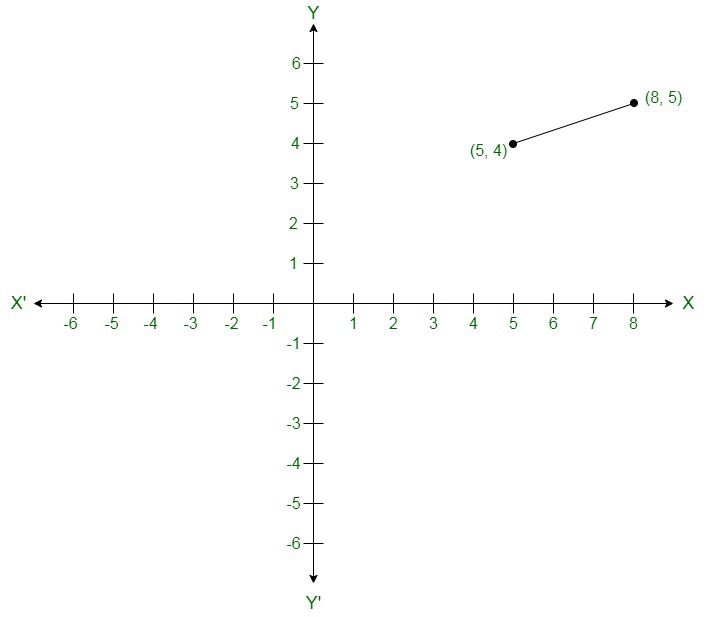
(viii) Given:
2y = – x + 1
2y = 1 – x
Now,
By putting x = 1 in 2y = 1 – x,
we get;
y = 0
Again, By putting x = 5 in 2y = 1 – x,
we get;
y = -2
On the graph:
Mark points (1, 0) and (5, -2) on the graph and join them.
问题2:给出通过(3,12)的两条直线的方程式。那里还有几条这样的线,为什么呢?
解决方案:
Since here, a = 3 and b = 12 is the solution of the equations.
Thus, we have to find the set of any two equations which will satisfy this point.
Assume 4a – b = 0 and 3a – b + 3 = 0 be the set of lines which are passing through (3, 12).
As we know that – infinite lines can be pass through a point.
Hence, there are infinite lines passing through (3, 12).
问题3:三轮代步车的首公里收费为15卢比,其后每公里收费8卢比。对于x公里的距离,将支付Rs y的金额。写出表示上述信息的线性方程式。
解决方案:
Consider, the total fare for covering the distance of ‘x’ km is given by Rs y
According to the problem given:
y = 15 + 8(x – 1)
y = 15 + 8x – 8
y = 8x + 7
Thus, the above equation represents the linear equation for the given data.
问题4:借阅图书馆的前三天收取固定费用,其后每天收取一笔额外费用。 Aarushi支付27卢比购买一本保存7天的书。如果固定费用为x卢比,每天费用为y卢比。写出表示上述信息的线性方程式。
解决方案:
As given: Aarushi paid Rs 27, of which Rs. x for the first three days and Rs. y per day for 4 more days is given by
x + (7 – 3) y = 27
x + 4y = 27
Thus, the above equation represents the linear equation for the given data.
问题5:数字比通过反转数字获得的数字多27。如果其单位和十进制数字分别为x和y,则写出表示该语句的线性方程式。
解决方案:
Given:
The original number is 27 more than the number obtained by reversing its digits
Thus the given number can be shown by 10y + x.
Number produced by reversing the digits of the number is 10x + y.
As per the problem:
10y + x = 10x + y + 27
10y – y + x – 10x = 27
9y – 9x = 27
9 (y – x) = 27
y – x = 3
x – y + 3 = 0
Thus, the above equation represents the linear equation for the given data.
问题6:一个两位数的总和和通过将其数字的顺序反转得到的数字为121。如果该数字的单位和十位数分别为x和y,则写出表示上述语句的线性方程式。
解决方案:
Given: The number is 10y + x.
After reversing the digits of the number,
We get,
10x + y
Sum of the two numbers is 121. (As given in the problem)
10y + x + 10x + y = 121
11x + 11y = 121
x + y = 11
Thus, the above equation represents the linear equation for the given data.
问题7:将点(3、5)和(-1、3)画在方格纸上,并验证通过这些点的直线是否也通过点(1、4)。
解决方案:
On the graph: Plot points (3, 5), (-1, 3) and (1, 4).
Consider A(1, 4), B(3, 5) and C(-1, 3)
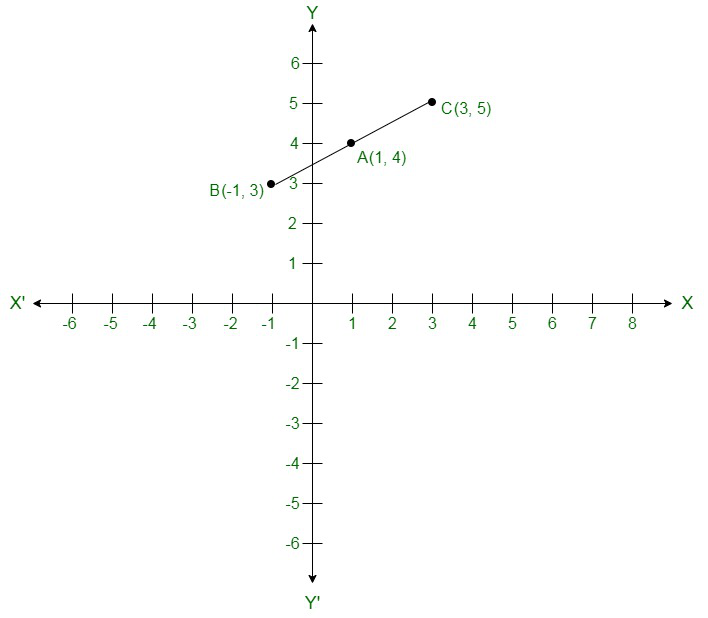
As per the above graph: We can see that, Point A (1, 4) is already plotted on the graph, and a point of intersection of two intersecting lines.
Therefore, it is proved that the straight line passing through (3, 5) and (-1, 3) and also passes through A (1, 4).
问题8:从下面给出的选择中,选择方程式,其图形如图所示。
(i)y = x
(ii)x + y = 0
(iii)y = 2x
(iv)2 + 3y = 7x
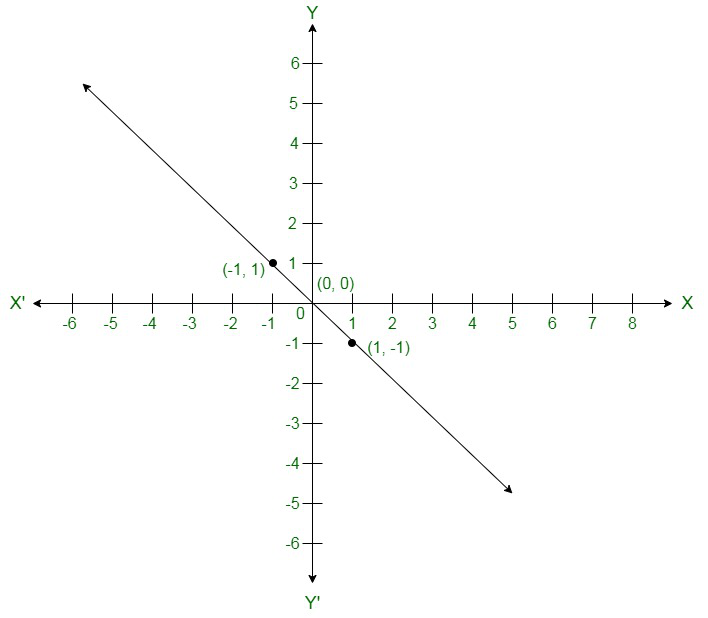
解决方案:
As per the given graph, co-ordinates (1, -1) and (-1, 1) are solutions of one of the equations.
Now, put the value of all the co-ordinates in each of the equation and verify which equation satisfy them.
(i) y = x
Put x = 1 and y = -1,
Thus, 1 ≠ -1
L.H.S ≠ R.H.S
By putting x = -1 and y = 1,
-1 ≠ 1
L.H.S ≠ R.H.S
Therefore,
y = x does not represent the graph in the given figure.
(ii) x + y = 0
Put x = 1 and y = -1,
⇒ 1 + (-1) = 0
⇒ 0 = 0
L.H.S = R.H.S
After putting x = -1 and y = 1,
(-1) + 1 = 0
0 = 0
L.H.S = R.H.S
Hence, the given solutions satisfy this equation.
(iii) y = 2x
Put x = 1 and y = -1
-1 = 2 (Can not be True)
Putting x = -1 and y = 1
1 = -2 (Can not be True)
Therefore, the given solutions does not satisfy this equation.
(iv) 2 + 3y = 7x
Put x = 1 and y = -1
2 – 3 = 7
-1 = 7 (Can not be true)
After putting x = -1 and y = 1
2 + 3 = -7
5 = -7 (Can not be True)
Therefore, the given solutions does not satisfy this equation.
问题9:从下面给出的选择中,选择方程式,其图形如下图所示:
(i)y = x + 2
(ii)y = x – 2
(iii)y = – x + 2
(iv)x + 2y = 6
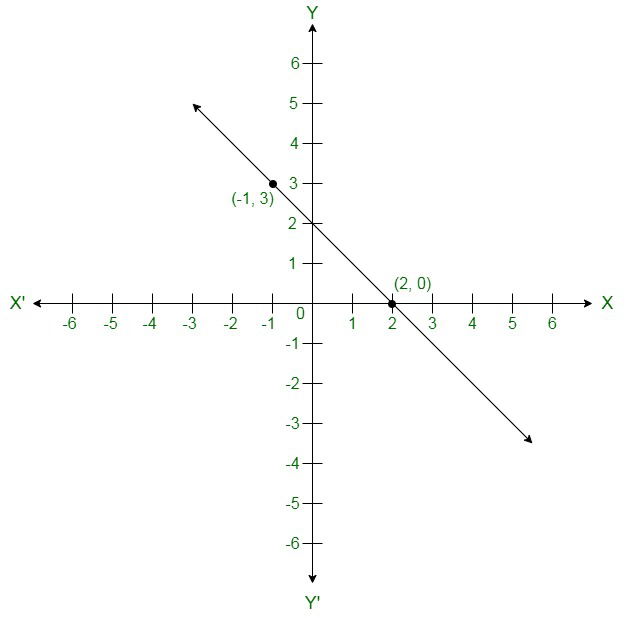
解决方案:
Given:
Here (-1, 3) and (2, 0) are the solution of one of the following given equations.
Verify that which of the equation satisfy both the points.
(i) y = x + 2
Put, x = -1 and y = 3
3 ≠ – 1 + 2
L.H.S ≠ R.H.S
By putting, x = 2 and y = 0
0 ≠ 4
L.H.S ≠ R.H.S
Hence, this solution does not satisfy the given equation.
(ii) y = x – 2
Put x = -1 and y = 3
3 ≠ – 1 – 2
L.H.S ≠ R.H.S
By putting, x = 2 and y = 0
0 = 0
L.H.S = R.H.S
Hence, the given solutions does not satisfy this equation completely.
(iii) y = – x + 2
Put x = – 1 and y = 3
3 = – (– 1) + 2
L.H.S = R.H.S
By putting x = 2 and y = 0
0 = -2 + 2
0 = 0
L.H.S = R.H.S
Thus, (0, 2) and (-1,3) satisfy this equation.
Therefore, this is the graph for equation y = -x + 2 .
(iv) x + 2y = 6
Put, x = – 1 and y = 3
-1 + 2(3) = 6
-1 + 6 = 6
5 = 6
L.H.S ≠ R.H.S
By putting x = 2 and y = 0
2 + 2(0) = 6
2 = 6
L.H.S ≠ R.H.S
Hence, this solution does not satisfy the given equation.
问题10:如果点(2,-2)位于线性方程的图形上,则5x + ky = 4,找到k的值。
解决方案:
Here point (2,-2) lies on the given linear equation, which implies (2, -2) satisfy this equation 5x + ky = 4.
So by putting x = 2 and y = -2 in 5x + ky = 4
5 × 2 + (-2) k = 4
10 – 2k = 4
2k = 10 – 4
2k = 6
k = ![]() = 3
= 3
The value of k is 3.