图是由节点和边组成的非线性数据结构。节点有时也称为顶点,边是连接图中任意两个节点的线或弧。在本文中,我们将了解图形表示方式之间的差异。
图主要可以用两种方式表示。他们是:
- 邻接表:邻接表是由所有链表的地址组成的数组。链表的第一个节点代表顶点,连接到这个节点的其余链表代表这个节点所连接的顶点。此表示还可用于表示加权图。链表可以稍微改变以存储边的权重。
- 邻接矩阵:邻接矩阵是一个大小为 V x V 的二维数组,其中 V 是图中的顶点数。设二维数组为 adj[][],槽 adj[i][j] = 1 表示从顶点 i 到顶点 j 有一条边。无向图的邻接矩阵总是对称的。邻接矩阵也用于表示加权图。如果 adj[i][j] = w,那么从顶点 i 到顶点 j 有一条边,权重为 w。
让我们考虑一个图来理解邻接表和邻接矩阵表示。设无向图为:
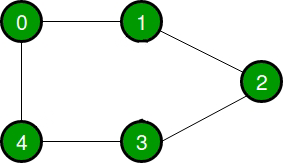
下图在上述表示中表示为:
- 邻接矩阵:在邻接矩阵表示中,图以二维数组的形式表示。数组的大小为V x V ,其中 V 是顶点集。下图表示邻接矩阵表示:

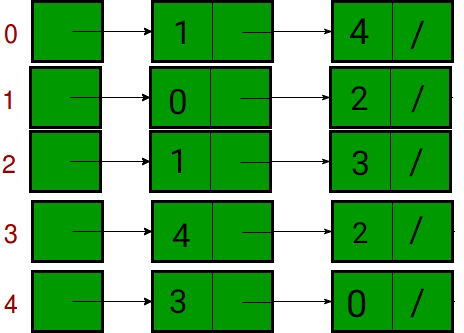
- 邻接表:在邻接表表示中,一个图被表示为一个链表数组。数组的索引代表一个顶点,其链表中的每个元素代表与该顶点形成边的顶点。下图表示邻接表表示:
下表描述了邻接矩阵和邻接表的区别:
桌子 {
表格布局:固定;
宽度:100%;
}
TD{
宽度:25%;
}
| Operations | Adjacency Matrix | Adjacency List |
|---|---|---|
| Storage Space | This representation makes use of VxV matrix, so space required in worst case is O(|V|2). | In this representation, for every vertex we store its neighbours. In the worst case, if a graph is connected O(V) is required for a vertex and O(E) is required for storing neighbours corresponding to every vertex .Thus, overall space complexity is O(|V|+|E|). |
| Adding a vertex | In order to add a new vertex to VxV matrix the storage must be increases to (|V|+1)2. To achieve this we need to copy the whole matrix. Therefore the complexity is O(|V|2). | There are two pointers in adjacency list first points to the front node and the other one points to the rear node.Thus insertion of a vertex can be done directly in O(1) time. |
| Adding an edge | To add an edge say from i to j, matrix[i][j] = 1 which requires O(1) time. | Similar to insertion of vertex here also two pointers are used pointing to the rear and front of the list. Thus, an edge can be inserted in O(1)time. |
| Removing a vertex | In order to remove a vertex from V*V matrix the storage must be decreased to |V|2 from (|V|+1)2. To achieve this we need to copy the whole matrix. Therefore the complexity is O(|V|2). | In order to remove a vertex, we need to search for the vertex which will require O(|V|) time in worst case, after this we need to traverse the edges and in worst case it will require O(|E|) time.Hence, total time complexity is O(|V|+|E|). |
| Removing an edge | To remove an edge say from i to j, matrix[i][j] = 0 which requires O(1) time. | To remove an edge traversing through the edges is required and in worst case we need to traverse through all the edges.Thus, the time complexity is O(|E|). |
| Querying | In order to find for an existing edge the content of matrix needs to be checked. Given two vertices say i and j matrix[i][j] can be checked in O(1) time. | In an adjacency list every vertex is associated with a list of adjacent vertices. For a given graph, in order to check for an edge we need to check for vertices adjacent to given vertex. A vertex can have at most O(|V|) neighbours and in worst can we would have to check for every adjacent vertex. Therefore, time complexity is O(|V|) . |
如果您希望与专家一起参加现场课程,请参阅DSA 现场工作专业课程和学生竞争性编程现场课程。