二分法与牛顿拉夫森法的区别
数值方法是通过将算术运算应用于数值方程的一组任务。我们可以制定数学问题来找到近似的结果。这个公式称为问题的数值实现。在这方面,不需要算法。然后为数值实现开发编程逻辑。编程通常使用一些高级语言,如 Fortran、Basic 等。
二分法
这种方法是基于中间值属性的重复应用。设f(x)是闭区间[x 1 , x 2 ]内的连续函数,若f(x 1 ), f(x 2 )符号相反,则区间(x)内至少有一个根α 1 , x 2 ),使得 f(α) = 0。

二分法
公式为: x 2 = (x 0 + x 1 ) / 2
牛顿拉夫森法
Newton Raphson 方法是确定方程 f(x)=0 的实根的过程,仅给出接近所需根的一点。
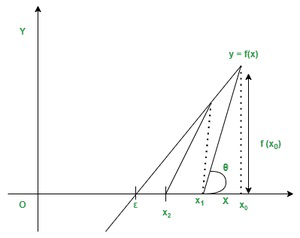
牛顿拉夫森法
公式为: x 1 = x 0 – f(x 0 )/f'(x 0 )
二等分法与牛顿拉夫森法的比较
| Sr. No. | Bisection Method | Newton Raphson Method |
|---|---|---|
| 1. | In the Bisection Method, the rate of convergence is linear thus it is slow. | In the Newton Raphson method, the rate of convergence is second-order or quadratic. |
| 2. | In Bisection Method we used following formula x2= (x0 + x1) / 2 | In Newton Raphson method we used following formula x1 = x0 – f(x0)/f'(x0) |
| 3. | In this method, we take two initial approximations of the root in which the root is expected to lie. | In this method, we take one initial approximation of the root. |
| 4. | The computation of function per iteration is 1. | The computation of function per iteration is 2. |
| 5. | The initial approximation is less sensitive. | The initial approximation is very sensitive. |
| 6. | In the Bisection Method, there is no need to find derivatives. | In the Newton Raphson method, there is a need to find derivatives. |
| 7. | This method is not applicable for finding complex, multiple, and nearly equal two roots. | This method is applicable for finding complex, multiple, and nearly equal two roots. |
问题 1:求方程 f(x) = x 3 – x – 1 的根
解决方案:
Given equation f(x) = x3 – x – 1
let x = 0, 1, 2
- In 1st iteration:
f(1) = -1 < 0 and f(2) = 5 > 0
The root lies between these two points 1 and 2
x0 = 1 + 2/2 = 1.5
f(x0) = f(1.5) = 0.875 > 0
- In 2nd iteration:
f(1) = -1 < 0 and f(1.5) = 0.875 > 0
The root lies between these two points 1 and 1.5
x1 = 1 + 1.5/2 = 1.25
f(x1) = f(1.25) = -0.29688 < 0
- In 3rd iteration:
f(1.25) = -0.29688 < 0 and f(1.5) = 0.875 > 0
The root lies between these two points 1.25 and 1.5
x2 = 1.25 + 1.5/2 = 1.375
f(x2) = f(1.375) = 0.22461 > 0
- In 4th iteration:
f(1.25) = -0.29688 < 0 and f(1.375) = 0.22461 > 0
The root lies between these two points 1.25 and 1.375
x3 = 1.25 + 1.375/2 = 1.3125
f(x3) = f(1.3125) = -0.05151 < 0
- In 5th iteration:
f(1.3125) = -0.05151 < 0 and f(1.375) = 0.22461 > 0
The root lies between these two points 1.3125 and 1.375
x4 = 1.3125 + 1.375/2 = 1.34375
f(x4) = f(1.34375) = 0.08261 > 0
- In 6th iteration:
f(1.3125) = -0.05151 < 0 and f(1.34375) = 0.08261 > 0
The root lies between these two points 1.3125 and 1.34375
x5 = 1.3125 + 1.34375/2 = 1.32812
f(x5) = f(1.32812) = 0.01458 > 0
- In 7th iteration:
f(1.3125) = -0.05151 < 0 and f(1.32812) = 0.01458 > 0
The root lies between these two points 1.3125 and 1.32812
x6 = 1.3125 + 1.32812/2 = 1.32031
f(x6) = f(1.32031) = -0.01871 < 0
- In 8th iteration:
f(1.32031) = -0.01871 < 0 and f(1.32812) = 0.01458 > 0
The root lies between these two points 1.32031 and 1.32812
x7 = 1.32031 + 1.32812/2 = 1.32422
f(x7) = f(1.32422) = -0.00213 < 0
- In 9th iteration:
f(1.32422) = -0.00213 < 0 and f(1.32812) = 0.01458 > 0
The root lies between these two points 1.32422 and 1.32812
x8 = 1.32422 + 1.32812/2 = 1.32617
f(x8) = f(1.32617) = 0.00621 > 0
- In 10th iteration:
f(1.32422) = -0.00213 < 0 and f(1.32617) = 0.00621 > 0
The root lies between these two points 1.32422 and 1.32617
x9 = 1.32422 + 1.32617/2 = 1.3252
f(x9) = f(1.3252) = 0.00204 > 0
- In 11th iteration:
f(1.32422) = -0.00213 < 0 and f(1.3252) = 0.00204 > 0
The root lies between these two points 1.32422 and 1.3252
x10 = 1.32422 + 1.3252/2 = 1.32471
f(x10) = f(1.32471) = -0.00005 < 0
The approximate root of the equation x3 – x – 1 = 0 using the Bisection method is 1.32471
问题 2:求方程 f(x) = 2x 3 – 2x – 5 的根
解决方案:
Given Equation f(x) = 2x3 – 2x – 5
- In 1st iteration:
f(1) = -5 < 0 and f(2) = 7 > 0
The root lies between these two points 1 and 2
x0 = 1 + 2/2 = 1.5
f(x0) = f(1.5) = 2 × 1.53 – 2 × 1.5 – 5 = -1.25 < 0
- In 2nd iteration:
f(1.5) = -1.25 < 0 and f(2) = 7 > 0
The root lies between these two points 1.5 and 2
x1 = 1.5 + 2/2 = 1.75
f(x1) = f(1.75) = 2 × 1.753 – 2 × 1.75 – 5 = 2.21875 > 0
- In 3rd iteration:
f(1.5) = -1.25 < 0 and f(1.75) = 2.21875 > 0
The root lies between these two points1.5 and 1.75
x2 = 1.5 + 1.75/2 = 1.625
f(x2) = f(1.625) = 2 × 1.6253 – 2 × 1.625 – 5 = 0.33203 > 0
- In 4th iteration:
f(1.5) = -1.25 < 0 and f(1.625) = 0.33203 > 0
The root lies between these two points 1.5 and 1.625
x3 = 1.5 + 1.625/2 = 1.5625
f(x3) = f(1.5625) = 2 × 1.56253 – 2 × 1.5625 – 5 = -0.49561 < 0
- In 5th iteration:
f(1.5625) = -0.49561 < 0 and f(1.625) = 0.33203 > 0
The root lies between these two points 1.5625 and 1.625
x4 = 1.5625 + 1.625/2 = 1.59375
f(x4) = f(1.59375) = 2 × 1.593753 – 2 × 1.59375 – 5 = -0.09113 < 0
- In 6th iteration:
f(1.59375) = -0.09113 < 0 and f(1.625) = 0.33203 > 0
The root lies between these two points 1.59375 and 1.625
x5 = 1.59375 + 1.625/2 = 1.60938
f(x5) = f(1.60938) = 2 × 1.609383 – 2 × 1.60938 – 5 = 0.1181 > 0
- In 7th iteration:
f(1.59375) = -0.09113 < 0 and f(1.60938) = 0.1181 > 0
The root lies between these two points 1.59375 and 1.60938
x6 = 1.59375 + 1.60938/2 = 1.60156
f(x6) = f(1.60156) = 2 × 1.601563 – 2 × 1.60156 – 5 = 0.0129 > 0
- In 8th iteration:
f(1.59375) = -0.09113 < 0 and f(1.60156) = 0.0129 > 0
The root lies between these two points 1.59375 and 1.60156
x7 = 1.59375 + 1.60156/2 = 1.59766
f(x7) = f(1.59766) = 2 × 1.597663 – 2 × 1.59766 – 5 = -0.03926 < 0
- In 9th iteration:
f(1.59766) = -0.03926 < 0 and f(1.60156) = 0.0129 > 0
The root lies between these two points 1.59766 and 1.60156
x8 = 1.59766 + 1.60156/2 = 1.59961
f(x8) = f(1.59961) = 2 × 1.599613 – 2 × 1.59961 – 5 = -0.01322 < 0
- In 10th iteration:
Here f(1.59961) = -0.01322 < 0 and f(1.60156) = 0.0129 > 0
The root lies between these two points 1.59961 and 1.60156
x9 = 1.59961 + 1.60156/2 = 1.60059
f(x9) = f(1.60059) = 2 × 1.600593 – 2 × 1.60059 – 5 = -0.00017 < 0
The Approximate root of the equation 2x3 – 2x – 5 = 0 using Bisection method is 1.60059
问题 3:求方程 f(x) = x 3 – x – 1 的根
解决方案:
Given equation x3 – x – 1 = 0
Using differentiate method the equation is
∴ f′(x) = 3x2 – 1
Here f(1) = -1 < 0 and f(2) = 5 > 0
∴ Root lies between 1 and 2
x0 = 1 + 2/ 2 = 1.5
- In 1st iteration:
f(x0) = f(1.5) = 0.875
f′(x0) = f′(1.5) = 5.75
x1 = x0 – f(x0) / f′(x0)
x1 = 1.5 – 0.875/ 5.75
x1 = 1.34783
- In 2nd iteration:
f(x1) = f(1.34783) = 0.10068
f′(x1) = f′(1.34783) = 4.44991
x2 = x1 – f(x1)/f′(x1)
x2 = 1.34783 – 0.10068/4.44991
x2 = 1.3252
- In 3rd iteration:
f(x2) = f(1.3252) = 0.00206
f′(x2) = f′(1.3252) = 4.26847
x3 = x2 – f(x2)/f′(x2)
x3 = 1.3252 – 0.00206/4.26847
x3 = 1.32472
- In 4th iteration:
f(x3) = f(1.32472) = 0
f′(x3) = f′(1.32472) = 4.26463
x4 = x3 – f(x3)/f′(x3)
x4 = 1.32472 – 0/ 4.26463
x4 = 1.32472
The Approximate root of the equation x3 – x – 1 = 0 using the Newton Raphson method is 1.32472
问题 4:求方程 f(x) = 2x 3 – 2x – 5 的根
解决方案:
Given equation 2x3 – 2x – 5 = 0
Using differentiate method the equation is
∴ f′(x) = 6x2 – 2
Here f(1) = -5 < 0 and f(2) = 7 > 0
∴ Root lies between 1 and 2
x0 = 1 + 2/ 2 = 1.5
- In 1st iteration:
f(x0) = f(1.5) = 2 × 1.53 – 2 × 1.5 – 5 = -1.25
f′(x0) = f′(1.5) = 6 × 1.52 – 2 = 11.5
x1 = x0 – f(x0)/f′(x0)
x1 = 1.5 – (-1.25)/11.5
x1 = 1.6087
- In 2nd iteration:
f(x1) = f(1.6087) = 2 × 1.60873 – 2 × 1.6087 – 5 = 0.1089
f′(x1) = f′(1.6087) = 6 × 1.60872 – 2 = 13.52741
x2 = x1 – f(x1)/f′(x1)
x2 = 1.6087 – 0.1089/13.52741
x2 = 1.60065
- In 3rd iteration:
f(x2) = f(1.60065) = 2 × 1.600653 – 2 × 1.60065 – 5 = 0.00062
f′(x2) = f′(1.60065) = 6 × 1.600652 – 2 = 13.37239
x3 = x2 – f(x2)/f′(x2)
x3 = 1.60065 – 0.00062/13.37239
x3 = 1.6006
The Approximate root of the equation 2x3 – 2x – 5 = 0 using the Newton Raphson method is 1.6006