问题1.阿希拉(Akhila)在她的村庄参加集市。她想享受乘坐巨轮的乐趣并玩Hoopla(一种游戏,在其中,您需要在货摊上的物品上扔一个钻机,如果戒指完全覆盖了任何物体,您就会得到它)。她参加Hoopla的次数是她在巨型飞轮上的骑行次数的一半。每次乘车费用为₹3,一场篮球比赛的费用为₹4。如果她在交易会上花费了₹20,请用代数和图形方式表示这种情况。
解决方案:
Let us assume the number of rides on the wheel to be x
And number of play of Hoopla to be y.
As per the given constraints,
x = 2y ⇒ x – 2y = 0 ….(i)
Cost of ride on wheel at the rate of Rs. 3 = 3x
Cost on Hoopla = 4y
Now, the total cost = Rs. 20
3x + 4y = 20 ….(ii)
Solving the equations (i) and (ii), we get,
Taking three points at-least of each line and connecting them to form a line. The point of intersection holds the solution, in this case.
From equation (i)
x = 2y
| x | 0 | 4 | 6 |
| y | 0 | 2 | 3 |
Similarly, in equation (ii)
3x + 4y = 20 ⇒ 3x = 20 – 4y
Computing the points for these lines,
| x | 4 | 0 | 8 |
| y | 2 | 5 | -1 |
Plotting these points and joining the point of intersection, we get the point (4, 2)
The unique solution is (4, 2).
Hence, we obtain, x = 4, y = 2

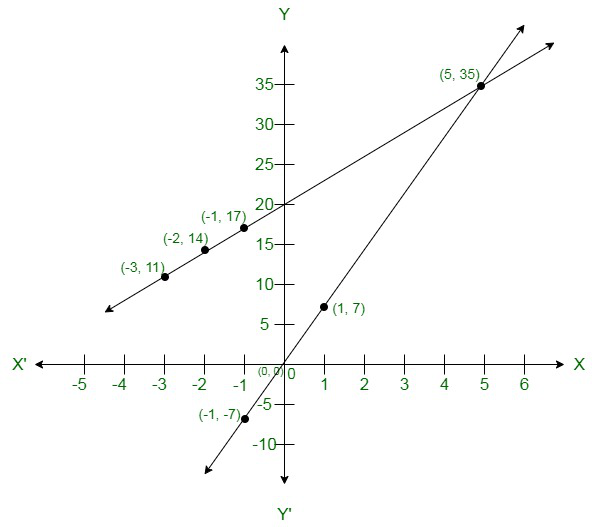
问题2:阿法塔布(Aftab)告诉他的女儿:“七年前,我的年龄是你的七倍。而且,从现在开始的三年后,我的年龄将是您的三倍。”这不是很有趣吗?用代数和图形方式表示这种情况。
解决方案:
Seven years ago :
Let us assume the age of Aftab’s daughter to be x years.
And, the age of Aftab to be y years.
Three years later,
Age of daughter = x + 10 years
Age of Aftab = y + 10 years
According to the given constraints,
y = 7x ⇒ 7x – y = 0 ……….(i)
y + 10 = 3 (x + 10)
=> y + 10 = 3x + 30
3x – y = 10 – 30 = -20
3x – y = -20 ….(ii)
The following equations are obtained :
7x – y = 0
3 x – y = -20
Solving these linear equations graphically :
7x – y = 0 ⇒ y = 7x
Plotting the points of the first line,
| x | 0 | 1 | -1 |
| y | 0 | 7 | -7 |
For the second equation, we get,
3x – y = -20
y = 3x + 20
Plotting the points of the second line,
| x | -1 | -2 | -3 |
| y | 17 | 14 | 11 |
Plotting these points and joining the point of intersection, we get the point (5, 35).
问题3.火车A的路径由等式3x + 4y-12 = 0给出,另一列火车B的路径由等式6x + 8y-48 = 0给出。以图形方式表示这种情况。
解决方案:
Given constraints are :
Path of A train is 3x + 4y – 12 = 0
and path of B train is 6x + 8y – 48 = 0
Computing the points for the line 3x + 4y- 12 = 0
| x | 4 | 0 | -4 |
| y | 0 | 3 | 6 |
Also, plotting the points for the second equation 6x+8y-48 =0.
| x | 8 | 4 | 0 |
| y | 0 | 3 | 6 |
Plotting these points graphically and joining the point of intersection, we get that the pair of lines are parallel.

问题4. Gloria沿着连接(-2,3)和(2,-2)的路径行走,而Suresh沿着连接(0,5)和(4,0)的路径行走。以图形方式表示这种情况。
解决方案:
We plot the points (-2, 3) and (2, -2) and connect them to form a line.
Also, we plot the points (0, 5), (4, 0) and connect them to obtain another line.
Graphically, we obtain, that these two lines are parallel to each other.

问题5.在比较比率而不绘制比率时,找出代表以下线性方程对的线在某点处相交,平行或重合:
(i)5x – 4y + 8 = 0
7x + 6y – 9 = 0
(ii)9x + 3y +12 = 0
18x + 6y + 24 = 0
(iii)6x – 3y +10 = 0
2x – y + 9 = 0
解决方案:
(i) We have the following pair of equations,
5x – 4y + 8 = 0
7x + 6y – 9 = 0
We have the following coefficients for these equations,
a1 = 5, b1 = -4, c1= 8
And, a2 = 7, b2= 6 and c2 = -9
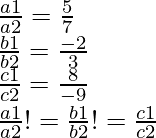
Therefore, these two lines intersect each other at a unique point.
(ii) We have the following pair of equations,
9x + 3y +12 = 0
18x + 6y + 24 = 0
We have the following coefficients for these equations,
a1 = 9, b1 = 3, c1= 12
And, a2 = 18, b2= 6 and c2 = 24
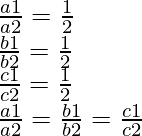
Therefore, these lines are coincident lines.
(iii) We have the following pair of equations,
6x – 3y +10 = 0
2x – y + 9 = 0
We have the following coefficients for these equations,
a1 = 6, b1 = -3, c1= 10
And, a2 = 2, b2= -1 and c2 = 9
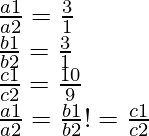
Therefore, these lines are parallel.
问题6.给定线性方程2x + 3y – 8 = 0,在两个变量中编写另一个线性方程,以使如此形成的对的几何表示为:
(i)相交线
(ii)平行线
(iii)重合线
解决方案:
We have the equation 2x+3y-8, now the coefficients are a1 = 2 , b1= 3 and c1 = -8 respectively.
(i) For intersecting pair of lines, the ratio of coefficients of the second equation should not be equal to the corresponding coefficients of the first.
So, Let us take a2 = 3, b2 = 4 and c2 = 2
that is, the second equation is 3x+4y+2 = 0
(ii) For parallel lines, we have,
a1/a2 = b1/b2 ≠ c1/c2
Therefore, a2/b2 can be 2/3.
Let us take a2 = 4 and b2 = 6,
that is, the second equation is 4x+6y+5 = 0
(iii) For coincident lines, we have,
a1/a2 = b1/b2 = c1/c2
that is, the second equation is 4x+6y – 16 = 0
问题7.发现每天2公斤苹果和1公斤葡萄的成本为卢比。 160.一个月后,4公斤苹果和2公斤葡萄的价格为卢比。 300.用代数和地理表示情况。
解决方案:
Let us assume the cost of 1kg of apples to be Rs. x
And, the cost of 1kg of grapes to be Rs. y
Now according to the given constraints, we obtain the following set of equations :
2x + y = 160
4x + 2y = 300
Now 2x + y = 160
y = 160 – 2x
Obtaining the points for this line :
| x | 20 | 40 | 60 |
| y | 120 | 80 | 40 |
The second equation, is 4x + 2y = 300
=> 2x + y = 150
=> y = 150 – 2x
Obtaining the points for this line :
| x | 40 | 50 | 60 |
| y | 70 | 50 | 30 |
Graphically, we obtain, that these two lines are parallel to each other.
