第10类RD Sharma解决方案-第1章实数–练习1.6

问题1.在没有实际执行长除法的情况下，请说明以下有理数将具有终止的十进制扩展数还是具有非终止的重复十进制扩展数。

(i)23/8

解决方案：

Denominator = 8 

⇒ 8 = 2³ x 5

The denominator 8 of the fraction 23/8 is of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 23/8 has terminating decimal expansion which terminates after three places of decimal.

(ii)125/441

解决方案：

Denominator = 441.

⇒ 441 = 3² x 7²

The denominator 441 of 125/441 is not of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, the fraction 125/441 has a non-terminating repeating decimal expansion.

(iii)35/50

解决方案：

Denominator = 50.

⇒ 50 = 2 x 5²

The denominator 50 of the fraction 35/50 is of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 35/50 has a terminating decimal expansion which terminates after two places of decimal.

(iv)77/210

解决方案：

Denominator = 210.

⇒ 210 = 2 x 3 x 5 x 7

The denominator 210 of the fraction 77/210 is not of the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 77/210 has non-terminating repeating decimal expansion.

(v)129 /(2 ² x 5 ⁷ x 7 ¹⁷ )

解决方案：

The denominator = 2² x 5⁷ x 7¹⁷.

The denominator of the fraction cannot be expressed in the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 125/441 has a non-terminating repeating decimal expansion.

(vi)987/10500

解决方案：

On reducing the above fraction, we have,

987/10500 = 47/500 (reduced form)

Denominator = 500.

⇒ 500 = 2² x 5³

The denominator 500 of 47/500 can be expressed in the form 2^m x 5ⁿ, where m, n are non-negative integers.

Therefore, 987/10500 has a terminating decimal expansion which terminates after three places of decimal.

问题2.通过以2m x 5n的形式写分母来写下以下有理数的十进制展开式，其中m和n是非负整数。

(i)3/8

解决方案：

Rational number is 3/8.

We can see that 8 = 2³ is of the form 2^m x 5ⁿ, where m = 3 and n = 0.

Therefore, the given number has terminating decimal expansion.

(ii)13/125

解决方案：

We can see that  125 = 5³ is of the form 2^m x 5ⁿ, where m = 0 and n = 3.

Therefore, the given rational number has terminating decimal expansion.

∴ 13/ 125 = (13 x 2³)/(125 x 2³) 

= 104/1000 

= 0.104

(iii)7/80

解决方案：

We can see, 80 = 2⁴ x 5 is of the form 2^m x 5ⁿ, where m = 4 and n = 1.

Therefore, the given number has terminating decimal expansion.

∴ 7/ 80 = (7 x 5³)/ (2⁴ x 5  x 5³)

 = 7 x  125 / (5 x  2)⁴ 

= 875/10000 

= 0.0875

(iv)14588/625

解决方案：

We can see, 625 = 5⁴ is of the form 2^m x 5ⁿ where m = 0 and n = 4.

So, the given number has terminating decimal expansion.

∴ 14588/ 625 = (14588 x 2⁴)/ (2⁴ x 5⁴ ) = 233408/10⁴ 

= 233408/10000 = 23.3408

(v)129 /(2 ² x 5 ⁷ )

解决方案：

We can see, 2² x 5⁷ is of the form 2^m x 5ⁿ, where m = 2 and n = 7.

So, the given number has terminating decimal expansion.

∴ 129/ 2² x 5⁷ = 129 x 2⁵ / 2² x 5⁷ x 2⁵

= 4182/10⁷

=4182/10000000

=0.0004182

问题3.以2m×5n的形式写有理数257/5000的分母，其中m，n是非负整数。因此，写出十进制扩展数，而不进行实际除法。

解决方案：

Denominator = 5000.

⇒ 5000 = 2³ x 5⁴

It’s seen that, 2³ x 5⁴ is of the form 2^m x 5ⁿ, where m = 3 and n = 4.

∴ 257/5000 = (257 x 2)/(5000 x 2) = 514/10000 = 0.0514 is the required decimal expansion.

问题4.关于以下有理数的分母的素因式分解，您能说什么：

(i)43.123456789

解决方案：

The number 43.123456789 has a terminating decimal expansion. Therefore, its denominator is of the form 2^m x 5ⁿ, where m, n are non-negative integers.

(ii) 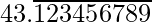$43.\overline{123456789}$ [Tex] [/ Tex]

解决方案：

The given rational has a non-terminating decimal expansion. Therefore, the denominator of the number has factors other than the numbers 2 or 5.

(iii) 27. \ overline {142857}

*** QuickLaTeX cannot compile formula:
 

*** Error message:
Error: Nothing to show, formula is empty

解决方案：

The given rational number has a non-terminating decimal expansion. Therefore, the denominator of the number has factors other than 2 or 5.

(iv)0.120120012000120000…。

解决方案：

Since 0.120120012000120000…. has a non-terminating decimal expansion. Therefore, the denominator of the number has factors other than 2 or 5.