11类NCERT解决方案-第9章序列和序列–练习9.3 |套装2

如果分别在^第4，^第10和一个GP的^第16^个方面是x，y和z，问题17。证明x，y，z在GP中

解决方案：

Let the first term of G.P. be a and common ratio be r.

According to the question 

a⁴ = ar³ = x   ……(1)

a₁₀ = ar⁹ = y   ……(2)

a₁₆ = ar¹⁵ = z    ……(3)  

Now divide eq(2) by (1), we get

ar⁹/ar³ = y /x

r⁶ = y /x

Divide eq(3) by (2), we get

ar¹⁵/ar⁹ = z/y

r⁶ = z/y

y /x = z/y              

So x, y, z are in G.P.

问题18.找到序列的n个项的总和，即8、88、888、8888…

解决方案：

According to the question 

Given Sequence: 8, 88, 888, 8888… 

This sequence is neither A.P. nor G.P. but we can change it into G.P. 

So, we can write as:

S_n = 8 + 88 + 888 + 8888 + … + n times

= 8(1 + 11 + 111 + 1111 + … + n times)

= 8/9(9 + 99 + 999 + 9999 + … + n times)

= 8/9((10 – 1) + (10² – 1) + (10³ – 1) + (10⁴ – 1) + … + n times)

= 8/9((10 + 10² + 10³ + 10⁴ + … + n times) – (1 + 1 + 1 + 1 + ….+ n terms))

As we know that, the sum of n terms of G.P. with 1^st term a & common ratio r is given by  

$S_n=\frac{a(r^n-1)}{r-1}$

=$\frac{8}{9}[\frac{10(10^n - 1)}{10 - 1}-n]$

= $\frac{8}{9}[\frac{(10^{n+1} - 10)}{9}-n]$

$S_n=\frac{80(10^n-1)}9-\frac{8n}9$

问题19：找到序列2、4、8、16、32和128、32、8、2、1 / 2的相应项的乘积总和。

解决方案：

According to the question 

Sequence 1: 2, 4, 8, 16, 32

Sequence 2: 128, 32, 8, 2, 1/2

Product of corresponding terms are

= 2 x 128, 4 x 32, 8 x 8, 16 x 2, 32 x 1/2  

= 256, 128, 64, 32, 16

So, the first term(a) = 256

Common ration = 1/2

S₅ = 256[1 – (1/2)⁵]/1/2

= 496

问题20：证明序列a，ar，ar ² ，… ar ^n-1和A，AR，AR ² ，… AR ^n-1的对应项的乘积形成一个GP，并求出公共比率。

解决方案：

According to the question 

Sequence 1: a, ar, ar² , …ar^{n – 1}

Sequence 2: A, AR, AR², … AR^{n – 1}

Prove: aA, arAR, ar²AR², …. ar^{n – 1}AR^{n – 1} from G.P

Now we find the common ration of the G.P

r = arAR. aA = rR

Again,

r = ar²AR²/arAR = rR

Hence, the sequence form G.P. and the common ratio is rR

问题21.查找四个形成几何级数的数字，其中第三项比第一项大9，而第二项比第四项大18。

解决方案：

Let us considered a be the first term, r be the common ratio and

four numbers in G.P. are a, ar, ar²,ar³

According to the question 

So, a₃ = a₁ + 9

ar² = ar + 9

ar² – ar = 9   ….(1)

a₂ = a₄ + 18  

ar = ar³ + 18  

ar – ar³ = 18   ….(2)

Now divide eq(2) by (1), we get

ar – ar³/ar² – ar = 18/9

ar (1 – r²)/-a(1 – r²) = 2

ar/-a = 2

r = -2

Now put the value of r in eq(1), we get the value of a

a(-2)² – a(-2) = 9

a = 3

Hence, the four numbers in G.P. are 3, 3(-2), 3(-2)²,3(-2)³

= 3, -6, 12, -24.

问题22.如果p ^th ，q ^th ， ^GP的第r个和第r个分别为a，b和c。证明a ^q–r b ^r–p c ^p–q = 1。

解决方案：

Let us considered the 1st term of a G.P. be k and common ratio x.

According to the question 

kx^p-1 = a      ….(1)

kx^q-1 = b      ….(2)

kx^r-1 = c      ….(3)

Prove: a^q–rb^r–pc^p–q = 1

Proof:

Lets take L.H.S

i.e., a^q–rb^r–pc^p–q 

Now put the value of a, b, c from the above equations,

 a^{q – r}b^{r – p}c^{p – q} = (kx^{p – 1})^{q – r}(kx^{q – 1})^{r – p}(kx^{r – 1})^{p – q} 

= k⁰ x x⁰

= 1

L.H.S = R.H.S

问题23.如果GP的第一个和第n个项分别是a和b，并且P是n个项的乘积，则证明P ² =(ab) ⁿ 。

解决方案：

According to the question 

The first term of the G.P. is a and the last term is b

Let the G.P. are a, ar, ar²,ar³. Here, r be the common ratio.

Then b = ar^n-1 

Now, Product of n terms(P) = a x ar x ar² x … x ar^n-1

P = aⁿr^{{1 + 2 + …n – 1}} 

P = aⁿr^{{(n(n – 1)/2}} 

So, P² = a²ⁿr^{(n(n – 1)} 

= [a²r^{(n – 1)}]ⁿ

= [a x ar^{(n – 1)}]ⁿ

= [ab]ⁿ

Hence Proved.

问题24.证明GP的前n个项之和与第(n +1)项^至第(2n)^个项的和之比为1 / r ⁿ 。

解决方案：

Let the first term of G.P. be a and the common ratio be r.

So, the sum of 1st n terms is $S_{1n}=\frac{a(r^n-1)}{r-1}$

According to the question

Sum of (n+1)^th to (2n)^th term is $S_{2n}=\frac{ar^n(r^n-1)}{r-1}$

The required ratio is:

 $\frac{S_{1n}}{S_{2n}}=\frac{\frac{a(r^n-1)}{r-1}}{\frac{ar^n(r^n-1)}{r-1}} =\frac{a(r^n-1)}{r-1} \times\frac{r-1}{ar^n(r^n-1)} = \frac{1}{r^n}$

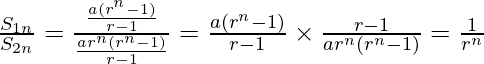
问题25.如果a，b，c和d在GP中，则表明(a ² + b ² + c ² )(b ² + c ² + d ² )=(ab + bc + cd) ²

解决方案：

According to the question 

a, b, c, d are in G.P., so let the common ratio of G.P.be r.

Then b = ar, c = ar², d = ar³ 

Simplifying LHS by putting value of b, c, d 

(a² + b² + c²)(b² + c² + d²) = (a² + a²r² + a²r⁴)(a²r² + a²r⁴ + a²r⁶)

= a⁴r²(1 + r² + r⁴)²

Now, simplifying RHS

(ab + bc + cd)² = (a²r + a²r³ + a²r⁵)² = a⁴r²(1 + r² + r⁴)²

LHS = RHS

问题26.在3到81之间插入两个数字，以便得到的序列为GP

解决方案：

Let us considered x1 and x2 be the two numbers in between 3 and 81. So, the G.P. is 3, x1, x2, 81 and

r be the common ratio. First term of the G.P.(a) = 3

So, a⁴ = 81

(3)r³ = 81

r³ = 27

r = 3

So, x1 = ar = 3 x 3 = 9

x2 = ar² = (3)(3)² = 27

Hence, the G.P. is 3, 9, 27, 81

问题27.找到n的值，以便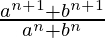$\frac{a^{n+1}+b^{n+1}}{a^n+b^n}$可以是a和b之间的几何平均值。

解决方案：

G.M. between a and b is √ab 

$\sqrt{ab}=\frac{a^{n+1}+b^{n+1}}{a^n+b^n}$

On squaring both side we get

$ab=\frac{(a^{n+1}+b^{n+1})^2}{(a^n+b^n)^2}$

ab(aⁿ + bⁿ)² = (a^{n + 1} + b^{n + 1})²

ab(a²ⁿ + b²ⁿ + 2aⁿbⁿ) = a^{2n + 2} + b^{2n + 2} + 2a^{2n + 2} b^{2n + 2} 

a²ⁿ⁺¹b + ab²ⁿ⁺¹ + 2aⁿ⁺¹bⁿ⁺¹ = a^{2n + 2} + b^{2n + 2} + 2a^{2n + 2} b^{2n + 2} 

ba²ⁿ⁺¹ + ab²ⁿ⁺¹ = a^{2n + 2} + b^{2n + 2}  

 ab²ⁿ⁺¹ – b^{2n + 2} = a^{2n + 2} – ba²ⁿ⁺¹ 

 ab²ⁿ⁺¹ – b^{2n + 2} = a^{2n + 2} – ba²ⁿ⁺¹

 b²ⁿ⁺¹ (a – b) = a^{2n + 1}(a – b) 

 b²ⁿ⁺¹ = a^{2n + 1}

 a²ⁿ⁺¹ / b^{2n + 1} = 1 = (a/b)⁰

 (a/b)^{2n + 1} = 1 = (a/b)⁰

2n + 1 = 0

n = -1/2

问题28.两个数字的和是其几何平均值的6倍，表明两个数字之比为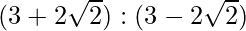$(3+2\sqrt2):(3-2\sqrt2)$

解决方案：

Let the two numbers be a and b.

And G.M. = √ab

According to the question 

a + b = 6√ab    …..(1)

Squaring on both side, we get

(a + b)² = 36(ab)

As we know that 

(a – b)² = (a + b)² – 4(ab)

So, 

(a – b)² = 36(ab) – 4(ab)

a – b = 4√2√ab  ……(2)

Now we add eq(a) and (2), we get

a + b + a – b = 6√ab + 4√2√ab

2a = √ab(6 + 4√2)

a = √ab(3 + 2√2)

Now put the value of a in eq(1), we get the value of b

 √ab(3 + 2√2) + b = 6√ab  

b = √ab(3 – 2√2)

Now we find the ratio:

a/b = √ab(3 + 2√2)/√ab(3 – 2√2)

= (3 + 2√2)/(3 – 2√2)

问题29.如果A和G分别是两个正数之间的AM和GM，请证明这些数字是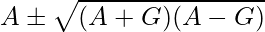$A\pm\sqrt{(A+G)(A-G)}$

解决方案：

Let the two numbers be a & b.

A.M = A= (a + b)/2

G.M = G = 2/√ab  

So, a + b = 2A   ….(1)

G² = ab  ….(2)

As we know that 

(a – b)² = (a + b)² – 4(ab)

So, 

(a – b)² = (2A)² – 4(G²)

(a – b)² = 4(A)² – 4(G²)

(a – b)² = 4[(A)² – (G²)]

(a – b)² = 4[(A – G)(A + G)]

(a – b) = √4[(A – G)(A + G)]

(a – b) = 2√(A – G)(A + G)  ……(3)

Now add eq(1) and (3), we get

2a = 2A + 2√(A – G)(A + G)

a = A + √(A – G)(A + G)

Now put the value of a in eq(1), we get

A + √(A – G)(A + G) + b = 2A 

b = A – √(A – G)(A + G) 

Hence, the two numbers are  A ± √(A – G)(A + G) 

问题30.某种文化中的细菌数量每小时增加一倍。如果最初在培养物中存在30种细菌，那么在第2小时，^第4小时和^第n小时结束时将存在多少细菌?

解决方案：

As the count of bacteria doubles after each hour, so at the end of n hours it becomes 2ⁿ times the original count.

So, first term(a) = 30, and common ratio(r) = 2

So, a₃ = ar² = (30)(2)² = 120 

At the end of 2^nd hour there are 120 bacteria.

a₄ = ar⁴ = (30)(2)⁴ = 480

At the end of 4^nd hour there are 480 bacteria.

a_n+1 = arⁿ = (30)(2)ⁿ 

At the end of n^nd hour there are (30)(2)ⁿ bacteria.

问题31.卢比将是多少。在存入一家银行后的10年内，年利率为10％的复合年利率为500?

解决方案：

In the end of 1st year, the amount = 500(1 + 1/10) = 500(1.1)

In the end of 2nd year, the amount = 500(1.1)(1.1)

In the end of 3rd year, the amount = 500(1.1)(1.1)(1.1)

…..So on

At the end of 10 year, the amount = 500(1.1)(1.1)(1.1)…….10 times

= 500(1.1)¹⁰

问题32.如果二次方程式的根的AM和GM分别为8和5，则求出二次方程式。

解决方案：

Let the roots of the quadratic equation be a and b.

According to the question 

A.M. = (a + b)/2 = 8 

a + b = 16

G.M. = √ab = 5

ab = 25

Then the quadratic equation using the roots can be written as 

x² – (a + b)x + ab = 0

Now put all these values in the quadratic equation, we get

x² – 16x + 25 = 0