11类NCERT解决方案-第9章序列和级数-第9章的其他练习|套装1

问题1表明的总和(M + N)^个和第(m – n)的AP的^第方面等于^第m^个项的两倍。

解决方案：

Let the first term and common difference of the A.P. be a and d respectively.

(m+n)^th term of the A.P. = a+(m+n−1)d

(m−n)^th term of the A.P. = a+(m−n−1)d 

Thus, L.H.S = a+(m+n−1)d + a+(m−n−1)d 

= 2a+(m+n−1+m−n−1)d

= 2a+(2m−2)d

= 2[a+(m−1)d] = 2a_m  

= R.H.S.

Hence, proved.

问题2.如果AP中三个数字的总和为24，乘积为440，则找到这些数字。

解决方案：

Let three numbers be a − d, a, a + d.

Sum of these numbers = 24

=> a−d+a+a+d = 24

=> 3a = 24

=> a = 8

Product of these numbers = 440

=> (a−d) a (a+d) = 440

=> (8−d) 8 (8+d) = 440

=> 64−d² = 55

=> d² = 9

=> d = ±3

When a=8, d=3, the numbers are 

8−3, 8, 8+3, i.e., 5, 8, 11

When a=8, d=−3, the numbers are

8+3, 8, 8-3, i.e., 11, 8, 5

问题3.令AP的n，2n，3n个项的总和分别为S ₁ ，S ₂和S ₃ ，表明S ₃ = 3(S ₂ – S ₁ )。

解决方案：

According to the question,

S₁ = Sum of n terms =n[2a+(n−1)d]/2

S₂ = Sum of 2n terms =  2n[2a+(2n−1)d]/2

S₃ = Sum of 3n terms = 3n[2a+(3n−1)d]/2 

Therefore, R.H.S.= 3(S₂−S₁) 

= $3\left[\frac{2n}{2}(2a+(2n−1)d)−\frac{n}{2}(2a+(n−1)d)\right]$

= $\frac{3n}{2}$[4a+(4n−2)d−2a−(n−1)d]

= $\frac{3n}{2}$[4a−2a+(4n−2−n+1)d]

= $\frac{3n}{2}$[2a+(3n−1)d]

= S₃ = L.H.S.

Hence, proved.

问题4.找出200到400之间的所有数字的总和，这些数字可以被7整除。

解决方案：

The numbers between 200 and 400 divisible by 7 form an A.P. with common difference(d)=7 and first term (a)=203.

Last term of this series will be, a_n = 399

We also know, a_n = a+(n−1)d

=> 399 = 203+(n−1)7

=> (n–1)7 = 196

=> n−1 = 28

=> n = 29

Sum of the series = $\frac{n}{2}$(a + a_n)

= $\frac{29}{2}$(203+399) = 8729

Therefore, required sum is 8729.

问题5.查找1到100的整数之和，该整数可被2或5整除。

解决方案：

Let S₁ be the sum of integers from 1 to 100 divisible by 2.

For S_1, Common difference(d)=2 and first term(a)=2

Last term will be, a_n = 100. Therefore,

=> 100 = 2+(n–1)2

=> n = 50

Hence, S₁ = $\frac{n}{2}$(a + a_n)

 = $\frac{50}{2}$[2+100] = 2550 

Let S₂ be the sum of integers from 1 to 100 divisible by 5.

For S_2, Common difference(d)=5 and first term(a)=5

Last term will be, a_n = 100

=> 100 = 5+(n–1)5

=> n = 20

Hence, S₂ = $\frac{20}{2}$[5+100] = 1050

Let S₃ be the sum of integers from 1 to 100 divisible by both 2 and 5.

For S₃, Common difference(d)=10 and first term(a)=10

Last term will be, a_n = 100

=> 100 = 10+(n–1)10

=> n = 10

Hence, S₃ = $\frac{10}{2}$[10+100] = 550

Required sum = S₁ + S₂ – S₃

= 2550 + 1050 – 550 

= 3050

问题6.找到所有两位数字的总和，将其除以4，得到1作为余数。

解决方案：

Two-digit numbers, which when divided by 4, yield 1 as remainder are:

13, 17, 21 … 97.

This series forms an A.P. with first term(a) = 13 and common difference(d) = 4.

Let n be the number of terms of the A.P.

We know the nth term of an A.P. is, a_n= a+(n–1)d

=> 97 = 13 + (n–1)4

=> 4(n–1) = 84

=> n = 22

Now, the sum of n terms of an A.P. is given by,

S_n = $\frac{n}{2}$[a + a_n]

= $\frac{22}{2}$[13+97] = 1210

Therefore, required sum is 1210.

问题7.如果f是用于所有的x，y∈N，使得F(1)一个满足函数f(X + Y)= F(X)F(Y)= 3和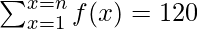$\sum_{x=1}^{x=n} f(x) = 120$ ，找到n的值。

解决方案：

We are given that,

f(x + y) = f(x) × f(y) for all x, y ∈ N … (1)

f(1) = 3

Putting x = y = 1 in (1), we have

f(1 + 1) = f(2) = f(1) f(1) = 3 × 3 = 9

Similarly,

f(1+1+1) = f(3) = f(1+2) = f(1) f(2) = 3 × 9 = 27

And, f(4) = f(1+3) = f(1) f(3) = 3 × 27 = 81

We have, f(1), f(2), f(3).., i.e., 3, 9, 27, …, 

This series forms a G.P. with the first term(a)=3 and common ratio(r)=3.

We know that sum of terms in G.P is given by,

S_n = $\frac{a(r^n -1)}{r-1}$

And also it’s given that the sum of terms of the function is 120.

=> 120 = $\frac{3(3^n-1)}{3-1}$

=> 3ⁿ–1 = 80 

=> n=4

Therefore, number of terms is 4.

问题8. GP的某些项的总和为315，其第一项和公比分别为5和2。查找最后一项和项数。

解决方案：

Let the total number of terms be n.

We know that, sum of terms of a G.P. is,

S_n = $\frac{a(r^n -1)}{r-1}$

Also, we know that the first term(a) is 5 and common ratio(r) is 2.

=> 315 = $\frac{5(2^n-1)}{2-1}$

=> 2ⁿ–1 = 63

=> n=6

The last term of the G.P = 6th term = ar^6-1 = (5)(2)⁵ = 160

Therefore, last term of the G.P. is 160 and the number of terms is 6.  

问题9. GP的第一项为1。第三项和第五项之和为90。找到GP的共同比率

解决方案：

Let the first term and common ratio of the G.P. be a and r respectively.

We have, a = 1. So,

a₃ = ar² = r²  …. (1)

a₅ = ar⁴ = r^{4 _..} …. (2)

According to the question, we have

a₃ + a₅ = 90

From (1) and (2),

r² + r⁴ = 90

r⁴ + r² – 90 = 0

Solving for r², we get,

$r^2 = \frac{-1+\sqrt{(1+360)}}{2} = \frac{-1±19}{2}$

r² = –10 or r² = 9

Taking only real roots, we get,

r = ±3

Therefore, the common ratio of the G.P. is ±3.

问题10. GP中三个数字的总和为56。如果我们从这些数字中依次减去1、7、21，我们将获得算术级数。查找数字。

解决方案：

Suppose the three numbers in G.P. are a, ar, and ar².

According to question, we have

=> a + ar + ar² = 56

=> a (1 + r + r²) = 56

=> a = $\frac{56}{(1+r+r^2)}$ …. (1)

Also, we are given that,

a – 1, ar – 7, ar² – 21 forms an A.P. 

which implies,

=> (ar – 7) – (a – 1) = (ar² – 21) – (ar – 7)

=> ar – a – 6 = ar² – ar – 14

=> ar² – 2ar + a = 8

=> a (r – 1)² = 8 ….. (2)

Putting value of a from (1) in (2), we get,

=> $\frac{56}{(1+r+r^2)}$(r – 1)² = 8

=> 7(r² – 2r + 1) = 1 + r + r²

=> 6r² – 15r + 6 = 0

=> (6r – 3) (r – 2) = 0

=> r = 2, 1/2

Now if r = 2, then a = 8 and the three numbers in G.P. are 8, 16, and 32.

If r = 1/2, then a = 32 and the three numbers in G.P. are 32, 16, and 8.

Therefore, in both the cases, the three numbers are 8, 16, and 32.  

问题11. GP由偶数个词组成。如果所有项的总和是占据奇数位的项的总和的5倍，则求出其公共比率。

解决方案：

Suppose the terms in the G.P. are a_1, a₂, a₃, a₄, … a_2n.

Number of terms = 2n

According to the question, we have

=> a₁ + a₂ + a₃ + …+ a_2n = 5 [a₁ + a₃ + … + a_2n–1]

=> a₁ + a₂ + a₃ + … + a_2n – 5 [a₁ + a₃ + … + a_2n–1] = 0

=> a₂ + a₄ + … + a_2n = 4 [a₁ + a₃ + … + a_{2n – 1}]      …. (1)

Now, let the terms of our G.P. be a, ar, ar², ar³, …..

Using sum of terms of a G.P., equation (1) becomes,

$\frac{ar(r^n-1)}{r-1} = \frac{4a(r^n-1)}{r-1}$

After solving we get,

ar = 4a

r = 4

Thus, the common ratio of the G.P. is 4.

问题12. AP的前四项之和为56。后四项之和为112。如果其第一项为11，则找到项数。

解决方案：

Suppose the terms in A.P. are a, a + d, a + 2d, a + 3d, … a + (n – 2) d, a + (n – 1)d.

According to the question, we have,

a = 11,

Sum of first four terms = a + (a + d) + (a + 2d) + (a + 3d) = 4a + 6d,

Sum of last four terms = [a + (n – 4) d] + [a + (n – 3) d] + [a + (n – 2) d] + [a + n – 1) d]

= 4a + (4n – 10) d

Then according to the given condition,

=> 4a + 6d = 56

=> 4(11) + 6d = 56

=> d = 2

Therefore, 4a + (4n –10)d = 112

=> 4(11) + (4n – 10)2 = 112

=> (4n – 10)2 = 68

=> 4n = 44

=> n = 11

Therefore, the number of terms of the A.P. is 11.

问题13。 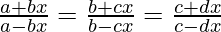$\frac{a+bx}{a-bx} = \frac{b+cx}{b-cx} = \frac{c+dx}{c-dx}$ ，然后显示a，b，c和d在GP中

解决方案：

We are given,

$\frac{a+bx}{a-bx} = \frac{b+cx}{b-cx}$

On cross multiplication, we have,

=> (a+bx)(b-cx) = (b+cx)(a-bx)

=> ab–acx+b²x–bcx² = ab–b²x+acx–bcx²

=> 2b²x = 2acx

=> b² = ac

=> b/a = c/b   ….. (1)

We are also given,

$\frac{b+cx}{b-cx} = \frac{c+dx}{c-dx}$

On cross multiplication, we have,

=> (b+cx)(c−dx) = (c+dx)(b−cx)

=> bc−bdx+c²x-cdx² = bc+bdx−c²x−cdx²

=> 2c²x = 2bdx

=> c² = bd

=> c/d = d/c   ….. (2)

From (1) and (2), we get

b/a = c/b = d/c

Therefore, a, b, c and d are in G.P.

问题14.设S为和，P为乘积， R为GP中n个项的倒数之和，证明P ² R ⁿ = S ⁿ 。

解决方案：

Suppose the terms in the G.P. are a, ar, ar², ar³, … ar^{n – 1}…

According to the question, we have,

S = a(rⁿ−1)/(r−1)  ….. (1)

P = aⁿ × r^1+2+….+n-1

= aⁿ r ^n(n-1)/2

R = 1/a + 1/ar + 1/ar² + …. + 1/ar^n-1

= $\left(\frac{ r^{n−1}}{r-1}\right)$[Tex]\left(\frac{1}{ar^{n-1}}\right)[/Tex]

So, P²Rⁿ = a²ⁿ r ^n(n-1) = $\frac{(r^n-1)^{n}}{a^nr^{n(n-1)}(r-1)^n}$

= $\frac{a^n(r^n-1)^n}{(r-1)^n}$

= $\left[\frac{a(r^n-1)}{r-1}\right]^{n}$

From (1), we get,

P²Rⁿ = Sⁿ

Hence, proved

问题15.^第p^个，^第q和r的AP的^第方面是a，b，c分别。证明(q – r)a +(r – p)b +(p – q)c = 0。

解决方案：

Let us take t and d to be the first term and the common difference of the A.P. respectively.

The n^th term of the A.P. is given by, a_n = t + (n – 1) d

Therefore,

p^th term will be, a_p = t+ (p – 1) d = a  ….. (1)

q^th term will be, a_q = t + (q – 1) d = b  ….. (2)

r^th term will be, a_r = t + (r – 1) d = c  ….. (3)

On subtracting equation (2) from (1), we get

=> (p – 1 – q + 1) d = a – b

=> (p – q) d = a – b

=> d = $\frac{a-b}{p-q}$ ….. (4)

On subtracting equation (3) from (2), we get

=> (q – 1 – r + 1) d = b – c

=> (q – r) d = b – c

=>  d = $\frac{b-c}{q-r}$ .…. (5)

Equating both the values of d obtained in (4) and (5), we get

=> $\frac{a-b}{p-q}$ = $\frac{b-c}{q-r}$

=> (a–b)(q–r) = (b–c)(p–q)

=> bp–cp+cq–aq+ar–br = 0

Rearranging terms, we get,

=> (–aq+ar)+(bp–br)+(–cp+cq) = 0  

=> a(q–r)+b(r–p)+c(p–q) = 0

Hence, proved

问题16。如果a(1 / b + 1 / c)，b(1 / c + 1 / a)，c(1 / a + 1 / b)在AP中，请证明a，b，c在AP中

解决方案：

We are given, a(1/b+1/c), b(1/c+1/a), c(1/a+1/b) are in A.P.

=> b(1/c+1/a)–a(1/b+1/c) = c(1/a+1/b)–b(1/c+1/a)

=> $\frac{b(a+c)}{ac}-\frac{a(b+c)}{bc} = \frac{c(a+b)}{ab}-\frac{b(c+a)}{ac}$

Multiplying both sides by abc and rearranging, we get,

=> b²a–a²b+b²c–a²c = c²a–b²a+c²b–b²c 

=> ab(b–a)+c(b²–a²) = a(c²–b²)+bc(c–b)

=> (b–a)(ab+bc+ca) = (c–b)(ab+bc+ca)

=> b–a = c–b

Therefore, a, b and c are in A.P.