11类NCERT解决方案-第9章序列和级数-第9章的其他练习|套装2

问题17。如果a，b，c，d在GP中，请证明(a ⁿ + b ⁿ )，(b ⁿ + c ⁿ )，(c ⁿ + d ⁿ )在GP中

解决方案：

We are given, a, b, c and d are in G.P.

Therefore, we have

b² = ac … (1)

c² = bd … (2)

ad = bc … (3)

We need to prove (aⁿ + bⁿ), (bⁿ + cⁿ), (cⁿ + dⁿ) are in G.P. i.e.,

=> (bⁿ+ cⁿ)² = (aⁿ + bⁿ) (cⁿ + dⁿ)

Solving L.H.S., we get

= b²ⁿ + 2bⁿcⁿ + c²ⁿ

= (b²⁾ⁿ + 2bⁿcⁿ + (c²)ⁿ

= (ac)ⁿ + 2bⁿcⁿ + (bd)ⁿ  [From (1) and (2)]

= aⁿcⁿ + bⁿcⁿ+ bⁿcⁿ + bⁿdⁿ

= aⁿcⁿ + bⁿcⁿ+ aⁿdⁿ + bⁿdⁿ  [From (3)]

= cⁿ(aⁿ + bⁿ) + dⁿ(aⁿ + bⁿ)

= (aⁿ + bⁿ) (cⁿ + dⁿ)

= R.H.S.

Therefore, (aⁿ + bⁿ), (bⁿ + cⁿ), and (cⁿ + dⁿ) are in G.P.

Hence, proved.

问题18。如果a和b是x ² – 3x + p = 0的根，而c，d是x ² – 12x + q = 0的根，那么a，b，c，d构成一个GP证明

(q + p)：( q – p)= 17:15。

解决方案：

We are given that a, b, c, d are in G.P. Let’s suppose the common ratio is r.

So, b=ar, c=ar² and d=ar³

Now a and b are the roots of x² – 3x + p = 0.

 Sum of roots = a + b = 3 

=> a + ar = 3 

=> a(1+r) = 3 ….. (1)

 Product of roots = ab = p

=> a(ar) = p

=> a²r = p  ….. (2)

And c, d are the roots of x² − 12x + q = 0

Sum of roots = c + d = 12

=> ar² + ar³ = 12

=> ar²(1+r) = 12  ….. (3)

Product of roots = cd = q

=> ar²(ar³) = q

=> a²r⁵ = q  ….. (4)

Dividing equation (3) by (1),we get,

=> $\frac{ar^2(1+r)}{a(1+r)}$ = $\frac{12}{3}$

=> r² = 4

=> r = ±2

When r=2, from (1), we get,

=> a(1+2) = 3

=> a = 1

Putting a=1 and r=2 in (2),

=> p = (1)²(2) = 2

From (4) we get,

q = (1)²(2)⁵ = 32

Now L.H.S. = $\frac{q+p}{q−p}$ = $\frac{32+2}{32−2}$ = $\frac{34}{30}$ = $\frac{17}{15}$ 

= R.H.S. 

When r=−2, from (1), we get,

=> a(1−2) = 3

=> a = −3

Putting a=−3 and r=−2 in (2),

p = (−3)²(−2) = −18

From (4) we get,

q = (−3)²(−2)⁵ = −288

Now L.H.S. = $\frac{q+p}{q−p}$ = $\frac{−288+(−18)}{−288−(−18)}$ = $\frac{−306}{−270}$ = $\frac{17}{15}$

= R.H.S.

Hence, proved.

问题19：两个正数a和b的AM和GM之比为m：n。证明a：b =(m +√(m ² -n ² )):(m-√(m ² -n ² ))。

解决方案：

We are given two numbers a and b. Therefore,

A.M = (a + b)/2 and G.M. = $\sqrt{(ab)}$

It’s given that, $\frac{a+b}{2\sqrt{(ab)}}$ = $\frac{m}{n}$

Applying Componendo and Dividendo on both sides, we get,

=> $\frac{a+b+2\sqrt{(ab)}}{a+b−2\sqrt{(ab)}}$ = $\frac{m+n}{m−n}$

=> $\frac{(\sqrt{a}+\sqrt{b})^2}{(\sqrt{a}−\sqrt{b})^2}$ = $\frac{m+n}{m−n}$

=> $\frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}−\sqrt{b}}$ = $\frac{\sqrt{(m+n)}}{\sqrt{(m−n)}}$

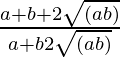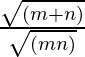
By again applying Componendo and Dividendo on both sides, we get,

=> $\frac{(\sqrt{a}+\sqrt{b}+\sqrt{a}−\sqrt{b})}{(\sqrt{a}+\sqrt{b}−\sqrt{a}+\sqrt{b})}$ = $\frac{\sqrt{(m+n)}+\sqrt{(m−n)}}{\sqrt{(m+n)}−\sqrt{(m−n)}}$

=> $\frac{\sqrt{a}}{\sqrt{b}}$ = $\frac{\sqrt{(m+n)}+\sqrt{(m−n)}}{\sqrt{(m+n)}−\sqrt{(m−n)}}$

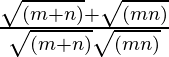
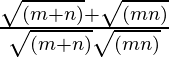
Squaring both sides, we get,

=>$\frac{a}{b}$ = $\frac{(m+n)+(m-n)+2\sqrt{(m+n)}\sqrt{(m−n)}}{(m+n)+(m-n)-2\sqrt{(m+n)}\sqrt{(m−n)}}$

=> $\frac{a}{b}$ = $\frac{2m+2\sqrt{(m^2−n^2)}}{2m-2\sqrt{(m^2−n^2)}}$

=> $\frac{a}{b}$ = $\frac{m+\sqrt{(m^2−n^2)}}{m-\sqrt{(m^2−n^2)}}$

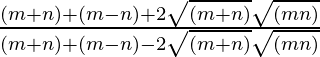
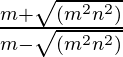
Hence, proved.

问题20：如果a，b，c在AP中； b，c，d在GP中，1 / c，1 / d，1 / e在AP中证明a，c，e在GP中

解决方案：

We are given that a, b, c are in A.P.

Hence, b – a = c – b  ….. (1)

And, given that b, c, d are in G.P.

So, c² = bd  ….. (2)

Also, we know 1/c, 1/d, 1/e are in A.P. Therefore,

=> 1/d – 1/c = 1/e – 1/d

=> 2/d = 1/c + 1/e   ….. (3)

We need to prove that a, c, e are in G.P.

From (1), we get

=> 2b = a + c

=> b = (a + c)/ 2

And from (2), we get

=> d = $\frac{c^2}{b}$

On putting above values in (3), we get,

=> $\frac{2b}{c^2}$ = 1/c + 1/e

=> $\frac{2(a+c)}{2c^2}$ = 1/c + 1/e

=> $\frac{a+c}{c^2}$ = $\frac{c+e}{ce}$

=> $\frac{a+c}{c}$ = $\frac{c+e}{e}$

=> (a+c)e = (c+e)c

=> ae+ce = c²+ec

=> c² = ae

Therefore, a, c, e are in G.P.

问题21.查找以下系列的和，最多n个项：

(i)5 + 55 + 555 +…

解决方案：

Let us take S_n = 5 + 55 + 555 + ….. up to n terms

Multiplying and dividing by 9, we get

= $\frac{5}{9}$[9+99+999+…to n terms]

= $\frac{5}{9}$[(10–1)+(10²–1)+(10³–1)…to n terms]

= $\frac{5}{9}$[(10+10²+10³+….n terms) – (1+1+1+…..n terms)]

= $\frac{5}{9}$
$\left[\frac{10(10^n-1)}{10-1}-n \right]$

= $\frac{5}{9}$
$\left[\frac{10(10^n-1)}{9}-n\right]$

= $\frac{50(10^n-1)}{81}$ – $\frac{5n}{9}$

(ii).6 + .66 + .666 +…

解决方案：

Let us take S_n = 0.6 + 0.66 + 0.666 + … up to n terms

= 6 [0.1+0.11+0.111+…up to n terms]

Multiplying and dividing by 9, we get

= $\frac{6}{9}$ [0.9+0.99+0.999+…up to n terms]

= $\frac{6}{9}$
$\left[\left(1-\frac{1}{10} \right)+\left(1-\frac{1}{10^2}\right)+\left(1-\frac{1}{10^3}\right)+...n\hspace{0.1cm}terms\right]$

= $\frac{2}{3}$
$\left[(1+1+1+...n\hspace{0.1cm}terms) - \frac{1}{10}\left(1+\frac{1}{10}+\frac{1}{10^2} +...n\hspace{0.1cm}terms\right)\right]$

= $\frac{2}{3}$
$\left[n-\frac{1}{10}\left[\frac{1-\left(\frac{1}{10}\right)^n}{1-\frac{1}{10}}\right]\right]$

= $\frac{2}{3}$– $\frac{2(1-10^{-n})}{27}$

问题22。找到系列2×4 + 4×6 + 6×8 +…+ n项的第20个项。

解决方案：

We are given the series: 2 × 4 + 4 × 6 + 6 × 8 + … n terms

nth term = a_n = 2n × (2n + 2) = 4n² + 4n

Putting n=20, we would get the 20th term,

a₂₀ = 4(20)² + 4(20) = 1600 + 80 = 1680

Therefore, the 20th term of the series is 1680.

问题23：找出该系列的前n个项的总和：3 + 7 + 13 + 21 + 31 +…

解决方案：

We are given the series: 3 + 7 + 13 + 21 + 31 + …

Let’s take S as the sum of this series. Therefore,

S = 3 + 7 + 13 + 21 + 31 + …+ a_n–1 + a_n     ….. (1)

S = 3 + 7 + 13 + 21 + …. + a_n–2 + a_n–1 + a_n ….. (2)

On subtracting (2) from (1), we get

=> S – S = [3 + (7 + 13 + 21 + 31 + …+ a_n–1 + a_n)] – [(3 + 7 + 13 + 21 + 31 + …+ a_n–1) + a_n]

=> 0 = 3 + [(7 – 3) + (13 – 7) + (21 – 13) + … + (a_n – a_n–1)] – a_n

=> a_n = 3 + [4 + 6 + 8 + … (n–1) terms]

As these series 4 + 6 + 8 + … (n–1) terms is an A.P., we can easily find its sum. Therefore,

= 3+$\frac{n-1}{2}[(2×4)+(n-1-1)2]$ 

= 3+$\frac{n-1}{2}[8+(n-2)2]$

= 3+(n–1)(n+2) 

= n²+n+1 

Now we have to summate our n^th term to find the sum(S_n) of this series.

$S_n = \sum_{k=1}^{k=n} a_k = \sum_{k=1}^{k=n} k^2 + \sum_{k=1}^{k=n} k + \sum_{k=1}^{k=n} 1$

S_n = $\frac{n(n+1)(2n+1)}{6}$ + $\frac{n(n+1)}{2}$ + n

= $\frac{n[(n+1)(2n+1)+3(n+1)+6]}{6}$

= $\frac{n[(n+1)(2n+1)+3(n+1)+6]}{6}$

= $\frac{n[2n^2+6n+10]}{6}$

= $\frac{n(n^2+3n+5)}{3}$

Therefore, sum of the series is $\frac{n(n^2+3n+5)}{3}$.

问题24.如果S ₁ ，S ₂ ，S ₃是前n个自然数的和，则它们的平方和立方体分别表示9S ₂ ² = S ₃ (1 + 8S ₁ )。

解决方案：

According to the question, we have,

S₁ = $\frac{n(n+1)}{2}$

S₂ = $\frac{n(n+1)(2n+1)}{6}$

S₃ = $\frac{n^2(n+1)^2}{4}$

Therefore, L.H.S. = 9S₂²

= 9 $\left[\frac{n(n+1)(2n+1)}{6}\right]^2$

= $\frac{[n(n+1)(2n+1)]^2}{4}$

And R.H.S. = S₃(1 + 8S₁)

= $\frac{n^2(n+1)^2}{4}$ $\left[1 + \frac{8n(n+1)}{2}\right]$

= $\frac{n^2(n+1)^2}{4}$ (1+ 4n² + 4n)

= $\frac{[n(n+1)(2n+1)]^2}{4}$

= L.H.S.

Hence, proved.

问题25.查找以下序列之和，最多n个项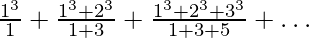： $\frac{1^3}{1} + \frac{1^3+2^3}{1+3} + \frac{1^3+2^3+3^3}{1+3+5} + …$

解决方案：

The n^th term of this series can be written as:

=> a_n = $\frac{\left[\frac{n(n+1)}{2}\right]^2}{[1+3+5+...+(2n-1)]}$

Here the denominator 1+3+5+…+(2n-1) is an A.P. 

with first term(a) 1,common difference 2 and last term 2n-1.

Total number of terms will be n. So,

1+3+5+7…+(2n–1) = $\left(\frac{n}{2}\right)[2×1+(n-1)2]$ = n²

Thus, our n^th term becomes,

a_n = $\frac{n^2(n+1)^2}{4n^2}$

= $\frac{(n+1)^2}{4}$

= $\frac{n^2}{4} + \frac{n}{2} + \frac{1}{4}$

Now we have to summate our n^th term to find the sum(S_n) of this series.

$S_n = \sum_{k=1}^{k=n} a_k = \sum_{k=1}^{k=n} \left(\frac{k^2}{4}+\frac{k}{2}+\frac{1}{4}\right)$

 = $\left(\frac{1}{4}\right)$
$\left[\frac{n(n+1)(2n+1)}{6}\right]$+ $\left(\frac{1}{2}\right)$
$\left[\frac{n(n+1)}{2}\right] + \frac{n}{4}$

= $\frac{n[(n+1)(2n+1)+6(n+1)+6]}{24}$

= $\frac{n(2n^2+3n+1+6n+6+6)}{24}$

= $\frac{n(2n^2+9n+13)}{24}$

Therefore, sum of the series is $\frac{n(2n^2+9n+13)}{24}$.

问题26.证明$\frac{1×2^2+2×3^2+...+n×(n+1)^2}{1^2×2+2^2×3+...+n^2×(n+1)} = \frac{3n+5}{3n+1}$ 。

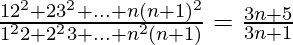解决方案：

We can see that,

The n^th term of the numerator = n(n + 1)² = n³ + 2n² + n

Now we have to summate this nth term to find the sum(S₁₎ of numerator. 

$S_1 = \sum_{k=1}^{k=n} (k^3+2k^2+k)$ 

= $\frac{n^2(n+1)^2}{4} + \frac{2n(n+1)(2n+1)}{6} + \frac{n(n+1)}{2}$

= $\frac{n(n+1)}{2} \left[\frac{n(n+1)}{2} + \frac{2(2n+1)}{3} + 1\right]$

= $\frac{n(n+1)}{2}\left[\frac{(3n^2+3n+8n+4+6)}{6}\right]$

= $\frac{n(n+1)}{2}\left[\frac{3n^2+11n+10}{6}\right]$

= $\frac{n(n+1)}{2}\left[\frac{(3n+5)(n+2)}{6}\right]$

= $\frac{n(n+1)(3n+5)(n+2)}{12}$

And n^th term of the denominator = n²(n + 1) = n³ + n²

Now we have to summate this n^th term to find the sum(S₂) of denominator. 

$S_2 = \sum_{k=1}^{k=n} (k^3+k^2)$

 = $\frac{n^2(n+1)^2}{4} + \frac{n(n+1)(2n+1)}{6}$

= $\frac{n(n+1)}{2}\left[\frac{n(n+1)}{2} + \frac{2n+1}{3}\right]$

= $\frac{n(n+1)}{2}\left[\frac{3n^2+3n+4n+2}{6}\right]$

= $\frac{n(n+1)}{2}\left[\frac{3n^2+7n+2}{6}\right]$

= $\frac{n(n+1)}{2}\left[\frac{(3n+1)(n+2)}{6}\right]$

= $\frac{n(n+1)(3n+1)(n+2)}{12}$

Now sum of the series(S) is equal to $\frac{S_1}{S_2}$

S = $\frac{\frac{n(n+1)(3n+5)(n+2)}{12}}{\frac{n(n+1)(3n+1)(n+2)}{12}}$

= $\frac{3n+5}{3n+1}$

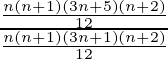
Hence, proved.

问题27.一位农民以12000卢比的价格购买了一辆二手拖拉机。他支付了6000卢比的现金，并同意按年支付500卢比的余额以及未付金额的12％的利息。拖拉机要给他多少钱?

解决方案：

We are given that the farmer pays Rs 6000 in cash.

So, the remaining unpaid amount = Rs 12000 – Rs 6000 = Rs 6000

According to the question, the total interest to be paid is,

Interest = 12% of 6000 + 12% of 5500 + 12% of 5000 + … + 12% of 500

= 12% of (6000 + 5500 + 5000 + … + 500)

Here the series 6000 + 5500 + 5000 + … + 500 is an A.P. with the first term a=6000 and common difference d=–500.

Let us take the number of terms of A.P. be n.

We know n^th term of an A.P. is given by, a_n = a+(n–1)d

=> 500 = 6000+(n-1)(–500)

=> 5500 = 500n–500

=> n = 12

Now,

The sum of the A.P = $\frac{12}{2}$ [2(6000) + (12–1)(-500)] 

= 6 [1200–5500] = 39000

Thus, the total interest to be paid = 12% of (6000 + 5500 + 5000 + … + 500)

= 12% of 39000 = Rs 4680

Therefore, the tractor will cost the farmer = (Rs 12000 + Rs 4680) = Rs 16680

问题28.沙姆沙德·阿里(Shamshad Ali)以22000卢比的价格购买了一辆小型摩托车，他支付了4000卢比的现金，并同意支付年度分期付款的余额1000卢比，外加10％的未付利息。滑板车要花多少钱?

解决方案：

We are given that Shamshad Ali buys a scooter for Rs 22000 and pays Rs 4000 in cash.

So, the remaining unpaid amount = Rs 22000 – Rs 4000 = Rs 18000

According to the question, the total interest to be paid,

Interest = 10% of 18000 + 10% of 17000 + 10% of 16000 + … + 10% of 1000

= 10% of (18000 + 17000 + 16000 + … + 1000)

Here, 18000, 17000, 16000 … 1000 forms an A.P. with first term a=18000 and common difference d=–1000.

Let’s take number of terms be n.

So, 1000 = 18000 + (n – 1) (–1000)

=> 17000 = 1000n–1000

=> n = 18

Now, the sum of the A.P. = $\frac{18}{2}$ [2(18000) + (18–1)(-1000)]

= 9 [36000–17000] = 9 [19000] = 171000

Thus, the total interest to be paid = 10% of (18000 + 17000 + 16000 + … + 1000)

= 10% of 171000 = Rs 17100

Thus, the cost of scooter = (Rs 22000 + Rs 17100) = Rs 39100

问题29.一个人给他的四个朋友写了一封信。他要求他们每个人都将信件复制并邮寄给四个不同的人，并指示他们以类似的方式移动链条。假设链条没有破裂，并且一封信的邮寄费用为50帕萨。找到邮寄第8套信件时在邮资上花费的金额。

解决方案：

The numbers of letters mailed forms a G.P. : 4, 4², … 4⁸ where first term, a = 4 and common ratio, r = 4

And the number of terms, n = 8

The sum of n terms of a G.P. is given by, S_n = $\frac{a(r^n-1)}{r-1}$

= $\frac{4(4^8-1)}{4-1}$

= $\left(\frac{4}{3}\right)$(65536–1) = 4(21845) = 87380

Now it’s given that the cost to mail one letter is 50 paisa.

Thus, Cost of mailing 87380 letters = Rs 87380 x (50/100) = Rs 43690

Therefore, the amount spent on the postage when 8th set of letter is mailed will be Rs 43690.

问题30.一名男子每年以5％的单利利率向银行存入10000卢比。自他存入款项后的第15年开始寻找金额，并计算20年后的总金额。

解决方案：

Given that the man deposited Rs 10000 in a bank at the rate of 5% simple interest annually.

Thus, the interest in first year = (5/100) x Rs 10000 = Rs 500

Now, Amount in 15th year = 10000 + (500+500+500+…14 times)

= Rs 10000 + 14 × Rs 500

= Rs 10000 + Rs 7000 = Rs 17000

Amount in 20th year = 10000 + (500+500+500+…20 times)

= Rs 10000 + 20 × Rs 500

= Rs 10000 + Rs 10000 = Rs 20000

Therefore, the amount in the 15th year is Rs 17000 and the total amount after 20 years will be Rs 20000.

问题31.一家制造商估计，一台价值15625卢比的机器的价值每年将贬值20％。找出5年末的估计值。

解决方案：

We are given the cost of machine is Rs 15625.

Also, given that the machine depreciates by 20% every year.

Therefore, its value after every year is 80% of the original cost i.e., 4/5th of the original cost.

So, the value at the end of 5 years = 15625 × $(\frac{4}{5} × \frac{4}{5} ×...\hspace{0.1cm}5\hspace{0.1cm}times)$ = 5 × 1024 = 5120

Thus, the value of the machine at the end of 5 years will be Rs 5120.

问题32：有150名工人在一定天数内完成工作。第二天有4名工人辍学，第三天又有4名工人辍学，依此类推。完成工作又花了8天的时间。查找完成工作的天数。

解决方案：

Let us take x to be the number of days in which 150 workers finish the work.

According to the question, we have

150x = 150 + 146 + 142 + ….. (x + 8) terms

We know, 150, 146, 142, ….. (x + 8) terms is an A.P.

 with first term (a) = 150, 

Common difference (d) = –4 and number of terms (n) = (x + 8)

Now, we know sum of this series is equal to 150$x$.

=> 150x = $\frac{(x+8)}{2}$[2×150 + (x+8–1)×4]

=> 300x = (x+8)(300–4x–28)

=> 300x = 272x–4x²+2176–32x

=> 4x²+60x+–2176 = 0

=> x²+15x–544 = 0

=> x²+32x–17x-544 = 0

=> (x+32)(x–17) = 0

=> x = –32 or 17

Ignoring x = –32 as number of days is a positive quantity so, x = 17.

It took 8 more days to finish the work because workers were dropped out. 

Hence, the number of days in which the work was completed is 17+8 = 25.