第11类RD Sharma解决方案–第2章关系–练习2.3 |套装2

问题12.设A = {x，y，z}和B = {a，b}。查找从A到B的关系总数。

解决方案：

The total number of relations that can be defined from a set A to a set B is the number of possible subsets of A × B. 

If n(A) = p and n(B) = q, then n(A × B) = pq. 

So, the total number of relations is 2^pq.

n(A) = 3 and n(B) = 2 ⇒ n(A × B) = 3 × 2 = 6

∴ Total number of relations = 2⁶ = 64

问题13。令R是从N到N的关系，由R = {((a，b)：a，b∈N and a = b ² }}定义。

以下陈述正确吗?

(i)(a，a)∈R对于所有a∈N

(ii)(a，b)∈R⇒(b，a)∈R

(iii)(a，b)∈R和(b，c)∈R⇒(a，c)∈R

解决方案：

Given:  R = {(a, b): a, b ∈ N and a = b²}.

(i) (a, a) ∈ R for all a ∈ N

Here, take b = 2

a = b² = 2² = 4

∴ (4, 2) R but (2, 2) ∉ R

As, 2² ≠ 2

So, 

No, the statement is false.

(ii) (a, b) ∈ R ⇒ (b, a) ∈ R

Here, take b = 2

a = b² = 2² = 4

∴ (4, 2) ∈ R but (2, 4) ∉ R

As, 4² ≠ 2

So,

No, the statement is false.

(iii) (a, b) ∈ R and (b, c) ∈ R ⇒ (a, c) ∈ R

Here, take b = 4

a = b² = 4² = 16

(16, 4)∈ R

Now, b = c²

4 = c²

c = -2 ∉ N 

(4, 2) ∈ R

But (16, 2) ∉ R

As, 2² ≠ 16

So,

No, the statement is false.

问题14.让A = {1,2,3，…。，14}。通过R = {(x，y)：3x – y = 0，其中x，y∈A}来定义集合A上的关系。使用箭头图描述这种关系。写下其域，共域和范围。

解决方案：

Given: R = {(x, y): 3x – y = 0, where x, y ∈ A}

A = {1, 2, 3,…,14}

As, y = 3x

∴ R = {(x, 3x): where x, 3x ∈ A}

R = {(1, 3×1), (2, 3×2), (3, 3×3), (4, 3×4)}

Note: We cannot include (5, 3×5) as 15 ∉ A

R = {(1, 3), (2, 6), (3, 9), (4, 12)}

So,

Domain of relation R = {1, 2, 3, 4}

Co-Domain of relation R = {1, 2, 3,…,14} = A

Range of relation R = {3, 6, 9, 12}

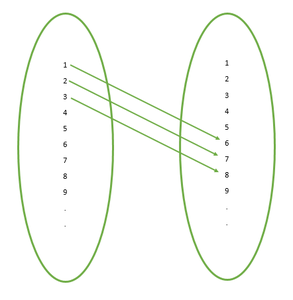
问题15：通过R = {(x，y)：y = x + 5，在自然数的集合N上定义关系R，x是自然数小于4，x，y∈N}。使用(i)名册形式(ii)箭头图描述这种关系。写下R的域和范围。

解决方案：

R = {(x, y): y = x + 5, x is a natural less than 4, x, y ∈ N}

Natural numbers less than 4 are 1, 2 and 3.

On putting x = 1, y = 1 + 5 = 6

On putting x = 2, y = 2 + 5 = 7

On putting x = 3, y = 3 + 5 = 8

(i) R = {(1, 6), (2, 7), (3, 8)}

(ii) The arrow diagram represent the relation(R):

So,

Domain of relation R = {1, 2, 3}

Range of relation R = {6, 7, 8}

问题16：A = {1,2,3,5}，B = {4,6,9}。通过R = {(x，y)定义从A到B的关系R：x和y之差为奇数，x∈A，y∈B}。以名册形式写R。

解决方案：

Given:

Relation R from A to B by R = {(x, y): the difference between x and y is odd, x ∈ A, y ∈ B}

A = {1, 2, 3, 5} and B = {4, 6, 9}

For x = 1:

y – x = 4 – 1 = 3 which is odd ⇒ 4 ∈ y

y – x = 6 – 1 = 5 which is odd ⇒ 6 ∈ y

y – x = 9 – 1 = 8 which is even ⇒ 8 ∉ y

For x = 2:

y – x = 4 – 2 = 2 which is even ⇒ 4 ∉ y

y – x = 6 – 2 = 4 which is even ⇒ 6 ∉ y

y – x = 9 – 2 = 7 which is odd ⇒ 8 ∈ y

For x = 3:

y – x = 4 – 3 = 1 which is odd ⇒ 4 ∈ y

y – x = 6 – 3 = 3 which is odd ⇒ 6 ∈ y

y – x = 9 – 3 = 6 which is even ⇒ 8 ∉ y

For x = 5:

x – y = 5 – 4 = 1 which is odd ⇒ 4 ∈ y

y – x = 6 – 5 = 1 which is odd ⇒ 6 ∈ y

y – x = 9 – 5 = 4 which is even ⇒ 8 ∉ y

∴ R = {(1, 4), (1, 6), (2, 8), (3, 4), (3, 6), (5, 4), (5, 6)}

Domain of relation R = {1, 2, 3, 5}

Range of relation R = {4, 6, 8}

问题17：以花名册形式写关系式R = {(x，x ³ )：x是小于10的质数。

解决方案：

Given: R = {(x, x³): x is a prime number less than 10}

Prime numbers less than 10 are 2, 3, 5 and 7

∴ R = {(2, 2³), (3, 3³), (5, 5³), (7, 7³)}

R = {(2, 8), (3, 27), (5, 125), (7, 343)}

So,

Domain of relation R = {2, 3, 5, 7}

Range of relation R = {8, 27, 125, 343}

问题18。令A = {1,2,3,4,5,6}。设R为与A定义的关系

R = {(a，b)：a，b∈A，b可被a整除}

(i)以花名册形式写R

(ii)找出R的域

(iii)找出R的范围。

解决方案：

Given:

R= {(a, b): a, b ∈ A, b is exactly divisible by a}

A= {1, 2, 3, 4, 5, 6}

Here,

6 is exactly divisible by 1, 2, 3 and 6

5 is exactly divisible by 1 and 5

4 is exactly divisible by 1, 2 and 4

3 is exactly divisible by 1 and 3

2 is exactly divisible by 1 and 2

1 is exactly divisible by 1

(i) R = {(1, 1), (2, 1), (2, 2), (3, 1), (3, 3), (4, 1), (4, 2),

             (4, 4), (5, 1), (5, 5), (6, 1), (6, 2), (6, 3), (6, 6)}

(ii) Domain of relation R = {1, 2, 3, 4, 5, 6}

(iii) Range of relation R = {1, 2, 3, 4, 5, 6}

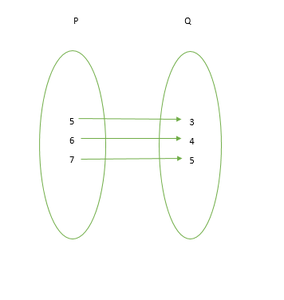
问题19。该图显示了集合P和Q之间的关系。将该关系写在

(i)设置建造者表格

(ii)名册表格

(iii)它的范围和范围是什么?

解决方案：

(i) Since 5 – 3 = 6 – 4 = 7 – 5 = 2

∴ x – y = 2 where x ∈ P and y ∈ Q

So,

R = {(x, y): x – y = 2, x ∈ P, y ∈ Q}

(ii) Now, R = {(5, 3), (6, 4), (7, 5)}

(iii) Domain of relation R = {5, 6, 7}

Range of relation R = {3, 4, 5}

问题20：设R是Z上由R = {((a，b)Z，a – b是整数}}所定义的关系。找到R的域和范围。

解决方案：

Given: R = {(a, b) ∈ Z, a – b is an integer}

Z denotes integer, and here a and b both are integers

We know that difference of two integers is always an integer

∴ a and b can be any integer in relation R

The domain of relation R = Z (as a ∈ Z)

The range of relation R = Z (as b ∈ Z)

问题21：对于由规则(a，b)∈R _{1 <=> 1 + ab> 0在R上定义的关系R 1} ，证明：(a，b)∈R ₁和(b，c)∈R _{1⇒(A，C)∈R 1}不是适用于所有的a，b，C∈R.

解决方案：

To prove: (a, b) ∈ R₁ and (b, c) ∈ R₁ ⇒(a, c)∈ R₁ is not true for all a, b, c R.

Given: R₁ = {(a, b)∈ R <=>1 + ab > 0}

Let a = 1, b = -0.5, c = -4

Here, (1, -0.5) ∈ R₁ [∵ 1+(1×-0.5) = 0.5 > 0]

And, (-0.5, -4) ∈ R₁ [∵ 1+(-0.5×-4) = 3 > 0]

But, (1, -4) ∉ R₁ [∵ 1+(1×-4) = -3 < 0]

∴ (a, b) ∈ R₁ and (b, c) ∈ R₁ ⇒(a, c) R₁ is not true for all a, b, c ∈ R

Hence, Proved.

Note: Here, R₁ is a relation whereas R denotes a real number.

问题22.设R是由(a，b)定义的N x N的关系R(c，d)对于所有(a，b)，(c，d)∈N的a + d = b + c xN。

显示：

一世。 (a，b)对所有(a，b)∈N x N的R(a，b)

ii。 (a，b)R(c，d)⇒(c，d)R(a，b)对所有(a，b)，(c，d)∈N x N

iii。 (a，b)R(c，d)和(c，d)R(e，f)⇒(a，b)所有(a，b)，(c，d)的R(e，f)，( e，f)∈N×N

解决方案：

Given:

(a, b) R (c, d) a + d = b + c for all (a, b), (c, d) ∈ N x N

(i) (a, b) R (a, b)

a + b = b + a for all (a, b) ∈ N x N

∴ (a, b) R (a, b) for all (a, b) ∈ N x N

(ii) (a, b) R (c, d)

a + d = b + c ⇒ c + b = d + a

(c, d) R (a, b) for all (c, d), (a, b) ∈ N x N

(iii) (a, b) R (c, d) and (c, d) R (e, f)

a + d = b + c and c + f = d + e

a + d + c + f = b + c + d + e

a + f = b + c + d + e – c – d

a + f = b + e

(a, b) R (e, f) for all (a, b), (c, d), (e, f) ∈ N × N