问题1:以下哪个数字不是理想的立方体?
(i)216(ii)128(iii)1000(iv)100(v)46656
解决方案:
(i) 216
Prime factorisation of 216 is:
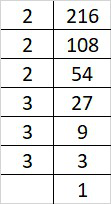
216 = 2×2×2×3×3×3
By forming groups in triplet of equal factors we get, 216 = (2×2×2)×(3×3×3)
Since, 216 can be grouped into triplets of equal factors i.e (2×3) = 6
Therefore, 216 is perfect cube of 6.
(ii) 128
Prime factorization of 128 is:
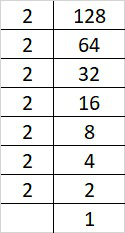
128 = 2×2×2×2×2×2×2
By forming groups in triplet of equal factors we get, 128 = (2×2×2)×(2×2×2)×2
Since, 128 cannot be grouped into triplets of equal factors.
Therefore, 128 is not a perfect cube.
(iii) 1000
Prime factorization of 1000 is:
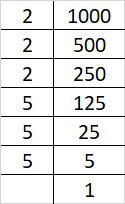
1000 = 2×2×2×5×5×5
By forming groups in triplet of equal factors we get, 1000 = (2×2×2)×(5×5×5)
Since, 1000 can be grouped into triplets of equal factors i.e (2×5) = 10
Therefore, 1000 is perfect cube of 10.
(iv) 100
Prime factorization of 100 is:
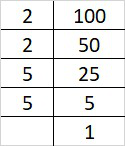
100 = 2×2×5×5
Since, 100 cannot be grouped into triplets of equal factors.
Therefore, 100 is not a perfect cube.
(v) 46656
Prime factorization of 46656 is:
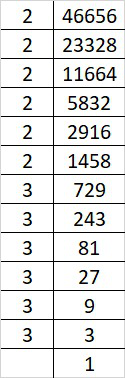
46656 = 2×2×2×2×2×2×3×3×3×3×3×3
By forming groups in triplet of equal factors we get, 46656 = (2×2×2)×(2×2×2)×(3×3×3)×(3×3×3)
Since, 46656 can be grouped into triplets of equal factors i.e (2×2×3×3) = 36
Therefore, 46656 is perfect cube of 36.
问题2:找出最小的数字,必须将每个数字乘以最小的数字,以获得一个完美的立方体。
(i)243(ii)256(iii)72(iv)675(v)100
解决方案:
(i) 243
Prime factorization of 243 is:
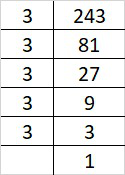
243 = 3×3×3×3×3
By forming groups in triplet of equal factors we get, 243 = (3×3×3)×3×3
Since, 3 cannot form a triplets of equal factors.
Therefore, 243 must be multiplied with 3 to get a perfect cube.
(ii) 256
Prime factorization of 256 is:
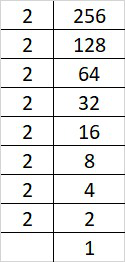
256 = 2×2×2×2×2×2×2×2
By forming groups in triplet of equal factors we get, 256 = (2×2×2)×(2×2×2)×2×2
Since, 2 cannot form a triplet of equal factors.
Therefore, 256 must be multiplied with 2 to get a perfect cube.
(iii) 72
Prime factorization of 72 is:
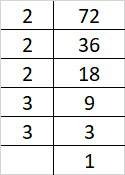
72 = 2×2×2×3×3
By forming groups in triplet of equal factors we get, 72 = (2×2×2)×3×3
Since, 3 cannot form a triplet of equal factors.
Therefore, 72 must be multiplied with 3 to get perfect cube.
(iv) 675
Prime factorization of 675 is:
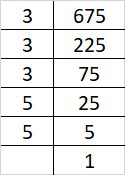
675 = 3×3×3×5×5
By forming groups in triplet of equal factors we get, 675 = (3×3×3)×5×5
Since, 5 cannot form a triplet of equal factors.
Therefore, 675 must be multiplied with 5 to get perfect cube.
(v) 100
Prime factorization of 100 is:
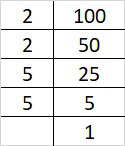
100 = 2×2×5×5
By forming groups in triplet of equal factors we get, 100 = 2×2×5×5
Since, 2 and 5 both cannot form a triplets of equal factors.
Therefore, 100 must be multiplied with 10 i.e 2×5 to get perfect cube.
问题3:找到最小的数字,必须将每个数字除以最小的数字,以获得一个完美的立方体。
(i)81(ii)128(iii)135(iv)192(v)704
解决方案:
(i) 81
Prime factorization of 81 is:
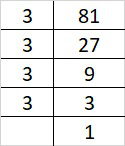
81 = 3×3×3×3
By forming groups in triplet of equal factors we get, 81 = (3×3×3)×3
Since, 3 cannot form a triplets of equal factors.
Therefore, 81 must be divided by 3 to get perfect cube.
(ii) 128
Prime factorization of 128 is:
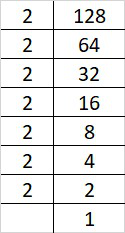
128 = 2×2×2×2×2×2×2
By forming groups in triplet of equal factors we get, 128 = (2×2×2)×(2×2×2)×2
Since, 2 cannot form a triplet of equal factors.
Therefore, 128 must be divided by 2 to get perfect cube.
(iii) 135
Prime factorization of 135 is:
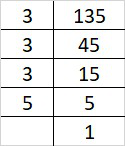
135 = 3×3×3×5
By forming groups in triplet of equal factors we get, 135 = (3×3×3)×5
Since, 5 cannot form a triplet of equal factors.
Therefore, 135 must be divided by 5 to get perfect cube.
(iv) 192
Prime factorization of 192 is:
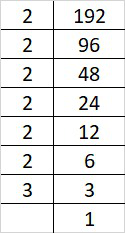
192 = 2×2×2×2×2×2×3
By forming groups in triplet of equal factors we get, 192 = (2×2×2)×(2×2×2)×3
Since, 3 cannot form a triplet of equal factors.
Therefore, 192 must be divided by 3 to get perfect cube.
(v) 704
Prime factorization of 704 is:
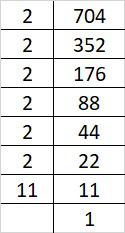
704 = 2×2×2×2×2×2×11
By forming groups in triplet of equal factors we get, 704 = (2×2×2)×(2×2×2)×11
Since, 11 cannot form a triplet of equal factors.
Therefore, 704 must be divided by 11 to get perfect cube.
问题4: Parikshit制作了一个长方形的橡皮泥,长5厘米,2厘米,5厘米。他需要多少个立方体来形成一个立方体?
解决方案:
Given: Side of cube are 5 cm, 2 cm and 5 cm.
Therefore, the volume of the cube = 5×2×5 = 50
We know that prime factorization of 50 is: 2×5×5
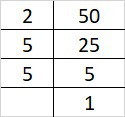
Since, 2 and 5 cannot form a triplet of equal factors.
Therefore, 50 must be multiplied with 20 i.e 2×2×5 to get perfect cube.
Hence, 20 cuboid is needed to make a perfect cube.