📅 最后修改于: 2021-06-25 07:44:21 🧑 作者: Mango
处于同一平面且不相交的线称为平行线。平行线之间的距离相等。当在一条线上的某个点绘制一条垂直线时,延伸时它也会与另一条线垂直相交。
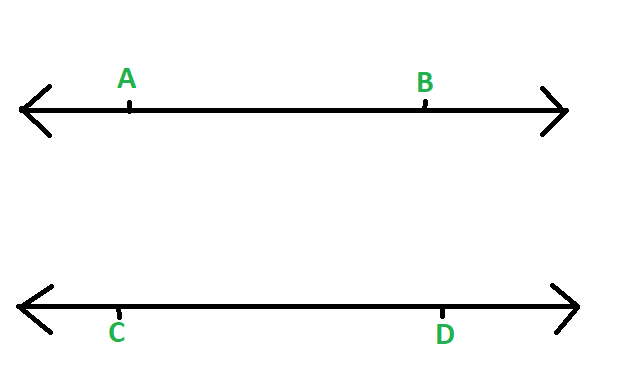
例子:
A点和C点之间的距离与B点和D点之间的距离相同。
图。1
定理:两条或多条平行于同一条线的线将彼此平行。
证明:
Let us assume that a line ‘a’ is parallel to line ‘b’ and the distance between line a and b is constant that is ‘x’ and another set of the parallel line is line ‘b’ and line ‘c’ with a constant distance of ‘y’. We have to prove that two or more lines that are parallel to one another are parallel to each other so in this case, we need to prove that if line ‘a’ is parallel to line ‘b’ and if line ‘b’ is parallel to line ‘c’ then we need to prove that line ‘a’ is parallel to line ‘c’.
As we are given that the constant distance between the parallel line ‘a’ and ‘b’ is x and the distance between line ‘b’ and ‘c’ is y. So as shown in the figure we can see the distance between the line ‘a’ and ‘c’ is x + y = z. And as we know that x and y are constant so the sum of 2 constant is also a constant. And we have proved that line ‘a’ and ‘c’ are parallel to one another.
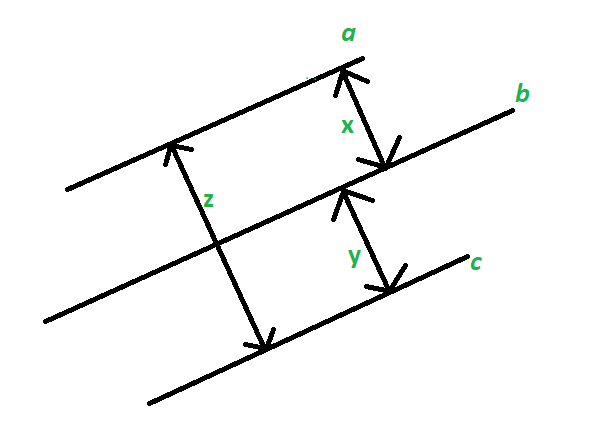
图2
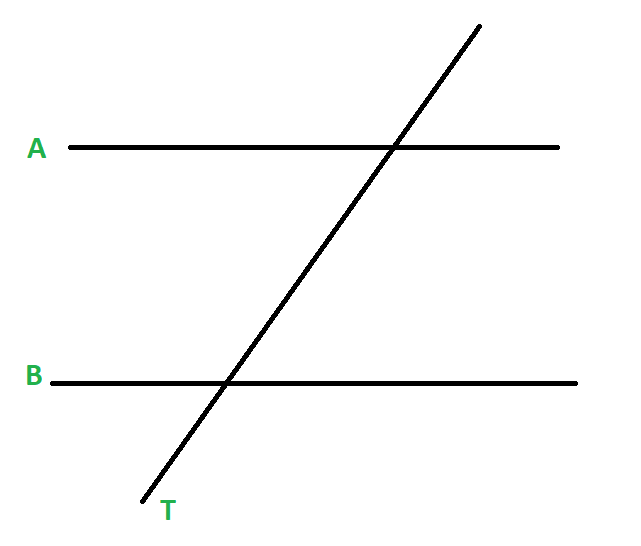
什么是横线?
位于两条或多条线的同一平面中并且在不同点处相交的任何线都称为横向线。根据Euclid的平行假设,如果两条线平行,则连续的内角是互补的,即它们之和为180度,相应的角度相等,交替的角度相等。
例子:
此处的线T为横线。
图3
横向线与平行线相交形成的角度
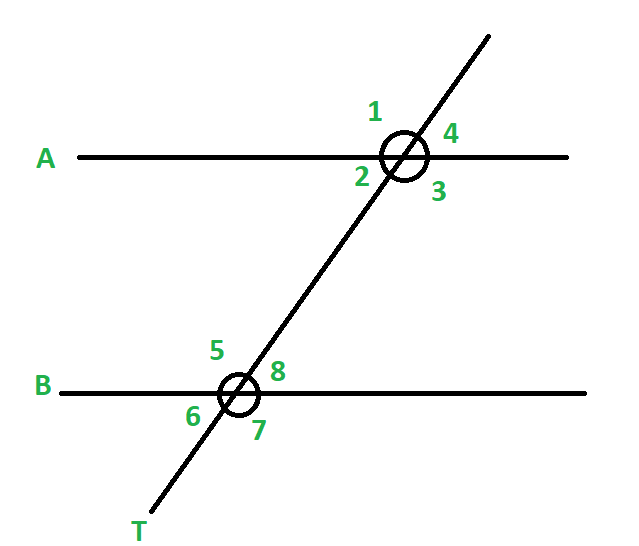
图4
对应角度
当两条或多条线被横向切割时,具有相同相对位置的角度称为对应角度。
例子:
In the above Fig 4
∠1 and ∠5
∠2 and ∠6
∠3 and ∠7
∠4 and ∠8 are corresponding angles.
连续的内部和外部角度
当一条线切割平行线时,位于横向线同一侧且在两条平行线内部的角度称为连续内角。
例子:
In the above Fig 4
∠2 and ∠5
∠3 and ∠8 are consecutive interior angles.
The angles which lie on the same side of the transversal line and outside the two parallel lines are called the consecutive exterior angles.
Example:- In the above Fig 4
∠1 and ∠6
∠4 and ∠7 are consecutive exterior angles.
补充角度
总计为180°的角度称为补充角度。由两条平行线形成的一对连续的内角和连续的外角称为补充角。
备用内角
当一条线切割平行线时,位于横向线两侧和两条平行线内部的角度称为交替内角。
例子:
In the above Fig 4
∠2 and ∠8
∠3 and ∠5 are alternate interior angles.
备用外角
当一条线切割平行线时,位于横向线两侧和两条平行线之外的角度称为备用外角。
例子:
In the above Fig 4
∠1 and ∠7
∠4 and ∠6 are alternate exterior angles.
同角
相同角度的角度称为全角。对应角和替代角也是全角。
三角形的角度和属性
定理1:三角形的角度和属性表示三角形的内角之和为180°。
证明:
Sum of all the angles of a triangle is equal to 180° this theorem can be proved by the below-shown figure. When we draw a line parallel to any given side of a triangle let’s make a line AB parallel to side RQ of the triangle. In the given figure as we can see that side RP and sie QP act as a transversal. So we can see that angle ∠APR = ∠PRQ and ∠BPQ = ∠PQR by the property of alternate interior angles we have studied above. Therefore we can prove that
∠APR + ∠RPQ + ∠BPQ = 180° and Hence ∠PRQ + ∠RPQ + ∠PQR = 180°
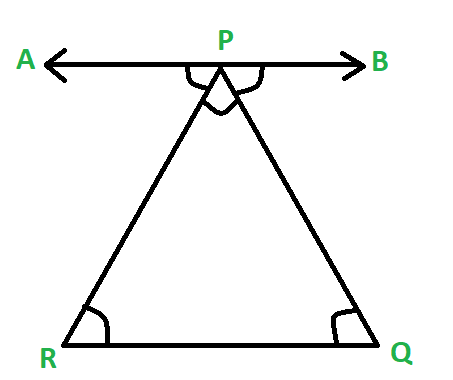
图5
示例:如果∠PQR= 30°,∠QRP= 70°,则使用三角形的角度总和找到角度量度?
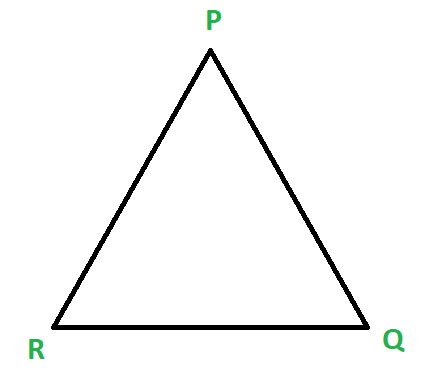
图6
解决方案:
As we know that ∠PQR + ∠QRP + ∠RPQ = 180°.Threfore 30° + 70° + ∠RPQ = 180°.
=> 100° + ∠RPQ = 180°
=> ∠RPQ = 180° – 100°
=> ∠RPQ = 80°
定理2:如果三角形的任意边都延伸了,那么形成的外角就是三角形两个相对的内角之和。
证明:
As we have proved the sum of all the interior angles of a triangle is 180° (∠ACB + ∠ABC + ∠BAC = 180°) and we can also see in figure 7 that ∠ACB + ∠ACD = 180° due to the straight line. By the above two equations, we can conclude that
=> ∠ACD = 180° – ∠ACB
=> ∠ACD = 180° – (180° – ∠ABC – ∠CAB)
=> ∠ACD = ∠ABC + ∠CAB
Hence proved that If any side of a triangle is extended, then the exterior angle so formed is the sum of the two opposite interior angles of the triangle.
示例:一个三角形的∠BAC= 60°,∠ABC= 60°,找到角度∠ACB的量度,如下图所示?
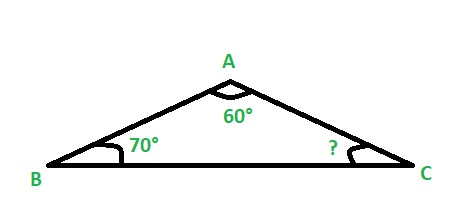
图7
解决方案:
解决此问题的方法有两种:
Method 1:
By angle sum property of a triangle we know ∠ACB + ∠ABC + ∠BAC = 180°
So therefore ∠ACB = 180° – ∠ABC – ∠BAC
=> ∠ACB = 180° – 70° – 60°
=> ∠ACB = 50°
Method 2:
By exterior angle sum property of a triangle, we know that ∠ACD = ∠BAC + ∠ABC
=> ∠ACD = 70° + 60°
=> ∠ACD = 130°
and, ∠ACB = 180° – ∠ACD
=> ∠ACB = 180° – 130°
=> ∠ACB = 50°
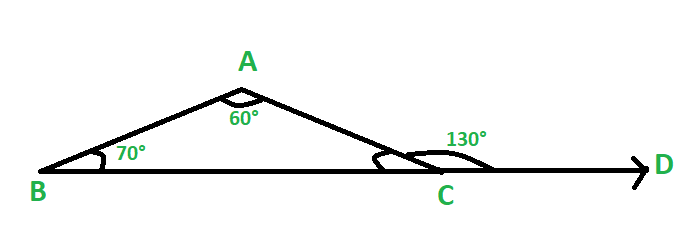
图8
例子:假设一条横切线切成一对平行线,:1:∠2= 4:5,如图9所示。找出?3的量度。

图9
解决方案:
As we are given that the given pair of a line are parallel so we can see that ∠1 and ∠2 are consecutive interior angles and we have already studied that consecutive interior angles are supplementary. Therefore let us assume the measure of ∠1 as ‘4x’ therefore ∠2 would be ‘5x’ as we are given that ∠1: ∠2 = 4: 5.
∠1 + ∠2 = 180°
=> 4x + 5x = 180°
=> 9x = 180°
=> x = 20°
Therefore ∠1 = 4x = 4 * 20° = 80° and ∠2 = 5x = 5 * 20° = 100°.
As we can clearly see in the figure that ∠3 and ∠2 are alternate interior angles so ∠3 = ∠2
∠3 = 100°.
示例:如图10所示,角度APQ = 120°,角度QRB = 110°。给定线AP与线RB平行,求出角度PQR的量度。
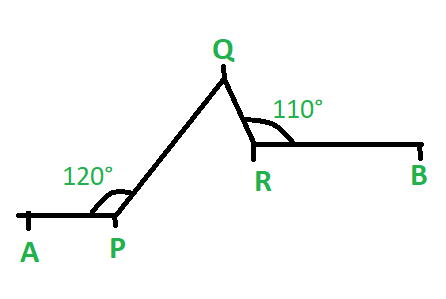
图10
解决方案:
As we are given that line AP is parallel to line AP so we know that the line perpendicular to one would surely be perpendicular to the other. So let us make a line perpendicular to both the parallel line as shown in the picture. Now as we can clearly see that ∠APM + ∠MPQ = 120° and as PM is perpendicular to line AP so ∠APM = 90° therefore angle ∠MPQ = 120° – 90° = 30°. Similarly, we can see that ∠ORB = 90° as OR is perpendicular to line RB therefore ∠QRO = 110° – 90° = 20°. Line OR is parallel to line QN and MP therefore ∠PQN = ∠MPQ as they both are alternate interior angles and similarly ∠NQR = ∠ORQ. Therefore ∠PQR = ∠PQN + ∠NQR
=> ∠PQR = 30° + 20°
=> ∠PQR = 50°
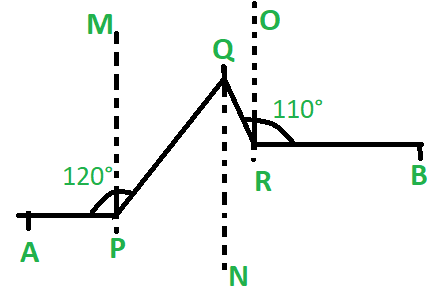
图11