设 A 为以下形式的 n × n 矩阵。

A 的行列式的值是多少?
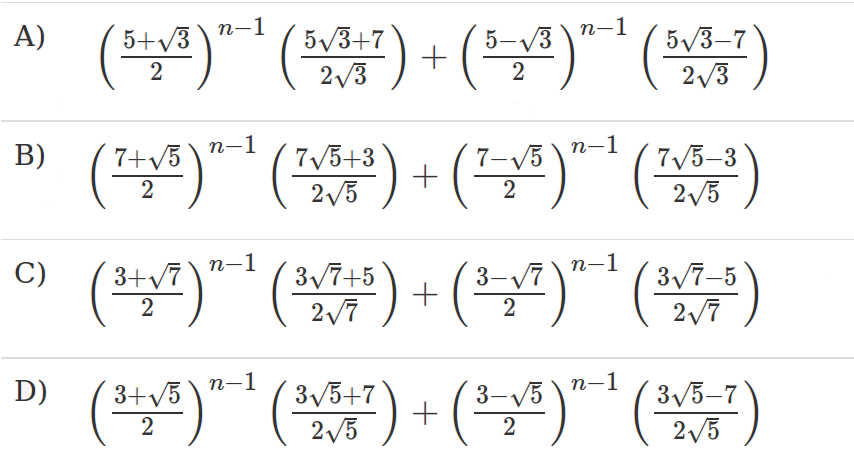
(一) A
(乙)乙
(C)丙
(四)丁答案: (D)
解释:
The first thing you need to get by seeing these type of questions is:-
Go for substitution method.
For n=2, the values will be
A) 16
B) 26
C) 7
D) 8
As all the values are unique for a small value of n, it does not take much time.
The given matrix will be A = [3 1]
[1 3]
So, det(A) = 3*3-1*1 = 8
Option (D) is the answer.
Alternative method:-
You can frame the relations in between det(An+1), det(An), det(An-1)
i.e. d(An+1) = 3*d(An) - d(An-1)
X = 3*X^0 - X^-1
X^2 = 3*x - 1
Solution for this equation is (3+sqrt(5))/2, (3-sqrt(5))/2
The only option which has roots of type (3+sqrt(5)) is D.
From this, you can match the options easily.
这个解释由Anil Saikrishna 提供。
这个问题的测验