两条线的交点公式

交点是两条直线或两条曲线相交的点。两条曲线的两条直线的交点是一点。如果两个平面相交，那么交点就是一条线。更准确地说，它被定义为满足两条曲线的两条直线或曲线的公共点，可以通过求解曲线方程得到。

如果我们考虑两条线 a ₁ x + b ₁ y + c ₁ = 0 和 a ₂ x + b ₂ y + c ₂ = 0 两条线的交点由下式给出：

Point of Intersection (x, y) = ((b₁×c₂ − b₂×c₁)/(a₁×b₂ − a₂×b₁), (c₁×a₂ − c₂×a₁)/(a₁×b₂ − a₂×b₁))

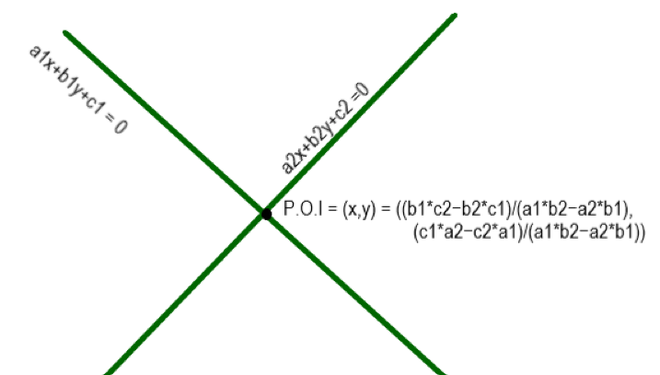
交点

两条线交点的推导：

Given equations:

a1x + b1y + c1 = 0 -> eq-1

a2x + b2y + c2 = 0 -> eq-2

Solving the equations using cross multiplication method:

       x     y     1

    b1    c1    a1    b1

    b2    c2    a2    b2

On cross-multiplying the constants we obtain:

x/(b1*c2 – b2* c1) = y/(c1*a2-c2*a1) = 1/(a1*b2-a2*b1)

Solving for x:

=> x/(b1*c2 – b2* c1) = 1/(a1*b2-a2*b1) 

=> x = (b1*c2 – b2* c1)/(a1*b2-a2*b1)

Solving for y:

=> y/(c1*a2-c2*a1) = 1/(a1*b2-a2*b1)

=> y=(c1*a2−c2*a1)/(a1*b2−a2*b1)

Hence point of intersection:

(x,y) = ((b₁×c₂ − b₂×c₁)/(a₁×b₂ − a₂×b₁), (c₁×a₂ − c₂×a₁)/(a₁×b₂ − a₂×b₁))

如果两条线平行，则它们永远不会相交：

Condition for two lines a1x + b1y + c1 = 0, a2x + b2y + c2 = 0 to be parallel 

 a1/b1 = a2/b2. 

示例问题

问题1：求直线3x + 4y + 5 = 0, 2x + 5y +7 = 0的交点。

解决方案：

The point of intersection of two lines is given by :

 (x, y) = ((b1*c2−b2*c1)/(a1*b2−a2*b1), (c1*a2−c2*a1)/(a1*b2−a2*b1))

 a1 = 3, b1 = 4, c1 = 5

 a2 = 2, b2 = 5, c2 = 7

 (x,y) = ((28-25)/(15-8), (10-21)/(15-8))

 (x,y) = (3/7,-11/7)

问题 2：求直线 9x + 3y + 3 = 0, 4x + 5y + 6 = 0 的交点。

解决方案：

The point of intersection of two lines is given by :

 (x,y) = ((b1*c2−b2*c1)/(a1*b2−a2*b1), (c1*a2−c2*a1)/(a1*b2−a2*b1))

 a1 = 9, b1 = 3, c1 = 3

 a2 = 4, b2 = 5, c2 = 6

 (x, y) = ((18-15)/(45-15), (54-12)/(45-15))

 (x, y) = (1/10, 7/5)

问题3：检查两条线是否平行 2x + 4y + 6 = 0, 4x + 8y + 6 = 0

解决方案：

To check whether the lines are parallel or not we need to check a1/b1 = a2/b2

a1 = 2, b1 = 4

a2 = 4, b2 = 8

2/4 = 4/8

1/2 = 1/2

Since the condition is satisfied the lines are parallel and can’t intersect each other.

问题4：检查两条线是否平行 3x + 4y + 8 = 0, 4x + 8y + 6 = 0

解决方案：

To check whether the lines are parallel or not we need to check a1/b1 = a2/b2

a1 = 3, b1 = 4

a2 = 4, b2 = 8

3/4 is not equal to 4/8

Since the condition is not satisfied the lines are not parallel.

问题 5：检查点 (3, 5) 是否是线 2x + 3y – 21 = 0, x + 2y – 13 = 0 的交点。

解决方案：

A point to be a point of intersection it should satisfy both the lines.

Substituting (x,y) = (3,5) in both the lines

Check for equation 1: 2*3 + 3*5 – 21 =0 —-> satisfied

Check for equation 2: 3 + 2* 5 -13 =0 —-> satisfied

Since both the equations are satisfied it is a point of intersection of both the lines.

问题6：检查点(2, 5)是否是线x + 3y – 17 = 0, x + y – 13 = 0的交点

解决方案：

A point to be a point of intersection it should satisfy both the lines.

Substituting (x,y) = (2,5) in both the lines

Check for equation 1: 2+ 3*5 – 17 =0 —-> satisfied

Check for equation 2: 7 -13 = -6  —>not satisfied

Since both the equations are not satisfied it is not a point of intersection of both the lines.

问题 7：找到线 x = -2 和 3x + y + 4 = 0 的交点

解决方案：

On substituting x = -2 in 3x + y + 4 = 0

-6 + y + 4 = 0;

y = 2;

So the point of intersection is (x,y) = (-2,2)