均匀带电无限平面片和薄球壳产生的电场

静电荷的研究是静电学的主题。通过形成电场，电荷会影响周围环境的特性。电场是充电系统的特性。卡尔·弗里德里希·高斯 (Karl Friedrich Gauss, 1777-1855) 是有史以来最伟大的数学家之一，他提出了高斯定律，它表达了电荷和电场之间的联系。其中，它代表了电场和电荷之间的联系，高斯定律等价于库仑定律。高斯定律为确定电强度表达式提供了一种可比较的方法。

什么是高斯定律？

高斯定律，通常称为高斯通量定理或高斯定理，是描述电荷分布与由此产生的电场之间关系的定律。

根据高斯定律，通过任何封闭表面的总电通量与所包含的电荷成正比。表面的电场是使用库仑方程确定的，但高斯定律对于计算封闭表面上的电场分布是必要的。它描述了封闭表面内包含的电荷或封闭封闭表面内存在的电荷。

The total flux contained within a closed surface equals 1/ε₀ times the total electric charge enclosed by the closed surface, according to Gauss Law.

The total charge enclosed in a closed surface is proportional to the total flux enclosed by the surface, according to the Gauss theorem. Therefore, if φ is total flux and ε₀ is electric constant, the total electric charge Q enclosed by the surface is,

Q = φ ε₀ 

Hence, the Gauss law formula is expressed in terms of charge as,

φ = Q / ε₀ 

where,

• Q is total charge within the given surface, and
• ε₀ is the electric constant.

The net flow through a closed surface is proportional to the net charge in the volume surrounded by the closed surface.

$\phi = \vec E\cdot d\vec A=\dfrac{q_{net}}{\epsilon_0}$

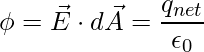
均匀带电无限平面片产生的电场

The electric field generated by the infinite charge sheet will be perpendicular to the sheet’s plane. Consider a cylindrical Gaussian surface whose axis is perpendicular to the sheet’s plane. Gauss’s Law may be used to calculate the electric field $(\vec E)$.

According to Gauss’s Law:

φ = Q / ε₀      …..(1)

Charge q will be σA as a result of continuous charge distribution. We shall only consider electric flow from the two ends of the hypothetical Gaussian surface when discussing net electric flux. This is due to the fact that the curved surface area and the electric field are perpendicular to each other, resulting in zero electric flux. As a result, the net electric flow will be:

φ = EA – (-EA) = 2EA

Therefore, from equation (1):

2EA = Q / ε₀

On rearranging for E as,

E = Q / 2ε₀

均匀带电无限平面片产生的电场

考虑半径“R”和表面电荷密度的薄球壳。贝壳表现出球对称性，通过观察可以看出。球壳产生的电场可以通过两种方式测量：

• 球壳外的电场
• 球壳内的电场

Electric Field Outside the Spherical Shell:

Consider a point P outside the spherical shell at a distance r from the centre of the spherical shell to determine an electric field outside the shell. We use a Gaussian spherical surface with radius r and centre O for symmetry. Because all points are equally spaced “r” from the sphere’s centre, the Gaussian surface will pass through P and experience a constant electric field all around. Then, according to Gauss’s law:

φ = q / ε₀     

Since a charge is enclosed inside the spherical Gaussian surface q, which is equal to σ × 4 πR². Therefore,

φ = σ × 4 πR² / ε₀         …..(1)

The total electric flux through the Gaussian surface will be:

φ = E × 4 πr²

So from equation (1):

σ × 4 πR² / ε₀ = E × 4 πr²

or

E = σ R² / ε₀ r²

Since, the surface charge density, σ is q / 4 πR². 

E = kq / r²

Electric Field Inside the Spherical Shell:

To find the electric field inside the spherical shell, consider a point P inside the shell. We pick the spherical Gaussian surface travelling through P, centred at O, and radius r by symmetry. Now, according to Gauss’ law,

φ = q / ε₀ 

Since the total electric flux inside the Gaussian surface will be:

φ = E × 4 πr² = 0

Hence, 

E = 0

示例问题

问题 1：将一个半径为 1 cm 的细长圆柱体置于水中，其电荷量为 5 μC/m。如果圆柱体浸入水中，求距圆柱体轴线 10 cm 处的电场强度。 (k_水= 81)

解决方案：

Given that,

q = 5 μC/m = 5 × 10^-6 C/m

R = 1 cm = 10^-2 m

r = 10 m = 10^-1 m

k_water = 81

The Electric field intensity at a point outside charged conducting cylinder is,

E = q / 2πkε₀ r

= 2q / 4πε₀ r

= (1 / 4πε₀) × q / kr  

= 9 × 10⁹ × (2 × 5 × 10^-6 / 81 × 10^-1)

= 1.111 × 10⁴ N/C

问题 2：半径为 2 cm 的长圆柱体在介电常数为 10 的介质中携带 5 µC/m 的电荷。求距离圆柱体轴 1 m 处的电场强度。

解决方案：

Given that,

R = 2 cm

σ = 5 μC/m

k =10

r = 1 m

Since, 

E = (1 / 4πε₀) × q / kr  

=  9 × 10⁹ × (2 × 5 × 10^-6 / 10 × 1)

= 9 × 10³ V/m 

问题3：表面电荷密度为5×10 ^-6 C/m ²的大平面电荷片位于空气中。求薄片附近的电场强度。

解决方案：

Given that,

σ = 5 × 10^-6 C/m²

ε₀ = 8.85 × 10^-2 C² /Nm²

k = 1

Electric field intensity near the sheet is,

E = σ / 2kε₀

= 5 × 10^-6 / (2  × 1 × 8.85 × 10^-12)

= 2.824 × 10⁵ N/C

问题 4：长度为 10 厘米的均匀带电圆柱体的电荷为 1 微库仑。如果是在介电常数为 5 的介质中，求圆柱外一点的强度。该点到圆柱体轴线的距离等于它的长度。

解决方案：

Given that,

ε₀ = 8.85 × 10^-12 C² / Nm²

l = 10cm = 0.1m

Q = 1μC = 10^-6 C

k = 5

r = l = 0.1m

Linear charge density is,

q = Q / l

= 10^-6 / 0.1

= 10^-5 C/m

Electric field intensity is,

E = (1 / 4πε₀) × q / kr  

= 9 × 10⁹ × (2 × 10^-5 / 5 × 10^-1)

= 3.6 × 10⁵ V/m    

问题 5：求一个大平面电荷的表面电荷，其电场强度接近 2.8 × 10 ⁵ N/C，保持在空气中。 (k_空气= 1)

解决方案：

Given that,

k_air = 1

E = 2.8 ×  10⁵ N/C

ε₀ = 8.85 × 10^-2 C² /Nm²

E = σ / 2kε₀

2.8 × 10⁵ N/C = σ × (2 × 8.85 × 10^-2)

= 4.95 × 10^-6 C /m²