10类RD Sharma解–第3章两个变量的线性方程对–练习3.11 |套装1

问题1.如果在一个矩形中，长度增加且宽度减少2个单位，则面积减少28个正方形。但是，如果长度减少1单位，宽度增加2单位，则面积增加33平方单位。找到矩形的区域。

解决方案：

Let’s assume the length and breadth of the rectangle be x unit and y unit.

Therefore, the area of rectangle = x * y sq. units

Given that,

Case 1:

Length is increased by 2 unit = New length is x+2 unit.

Breadth is reduced by 2 unit = New breadth is y-2 unit.

Area is reduced by 28 square units i.e. = (x * y) – 28

therefore the equation becomes,

= (x+2)(y−2) = xy − 28

= xy − 2x + 2y – 4 = xy − 28

= −2x + 2y – 4 + 28 = 0

= 2x − 2y – 24 = 0 —————(i)

Case 2:

Length is reduced by 1 unit = New length is x-1 unit.

Breadth is increased by 2 unit = New breadth is y+2 unit.

Area is increased by 33 square units i.e. = (x * y) + 33

therefore the equation becomes,

(x−1)(y+2) = xy + 33

= xy + 2x – y – 2 = x + 33

= 2x – y − 2 − 33 = 0

= 2x – y −35 = 0 ———————(ii)

Now by solving equation (i) and (ii) we get,

x = 46/2 = 23

and,

y = 22/2 = 11

Hence,

The length of the rectangle is 23 unit.

The breadth of the rectangle is 11 unit.

therefore, the area of the actual rectangle = length x breadth,

= x * y = 23 x 11 = 253 sq. units

Therefore, the area of rectangle is 253 sq. units.

问题2.如果将长度增加7米，而将宽度减少3米，则矩形的面积将保持不变。如果长度减少7米，宽度增加5米，则该区域不会受到影响。找到矩形的尺寸。

解决方案：

Let’s assume the length and breadth of the rectangle be x unit and y unit.

therefore, the area of rectangle = x * y sq. units

Given that,

Case 1:

Length is increased by 7 meter = New length is x+7

Breadth is decreased by 3 meter = New breadth is y-3

Area of the rectangle remains same i.e. = x * y.

therefore, the equation becomes,

xy = (x+7)(y−3)

xy = xy + 7y − 3x − 21

3x – 7y + 21 = 0 —————-(i)

Case 2:

Length is decreased by 7 meter = New length is x-7

Breadth is increased by 5 meter = New breadth is y+5

Area of the rectangle still remains same i.e. = x * y.

therefore, the equation becomes

xy = (x−7)(y+5)

xy = xy − 7y + 5x − 35

5x – 7y – 35 = 0 —————–(ii)

Now by solving equation (i) and (ii) we get,

x = 392/14 = 28

And,

y = 210/14 = 15

Therefore, the length of the rectangle is 28 m. and the breadth of the actual rectangle is 15 m.

问题3.在矩形中，如果将长度增加3米，而将宽度减小4米，则三角形的面积将减少67平方米。如果长度减少1米，宽度增加4米，则面积增加89平方米。找到矩形的尺寸。

解决方案：

Let’s assume the length and breadth of the rectangle be x units and y units respectively.

therefore, the area of rectangle = x * y sq. units

Given that,

Case 1:

Length is increased by 3 meter = New length is x+3

Breadth is reduced by 4 meter = New breadth is y-4

Area of the rectangle is reduced by 67 m2 = (x * y) – 67.

therefore, the equation becomes

xy – 67 = (x + 3)(y – 4)

xy – 67 = xy + 3y – 4x – 12

4xy – 3y – 67 + 12 = 0

4x – 3y – 55 = 0 —————-(i)

Case 2:

Length is reduced by 1 meter = New length is x-1

Breadth is increased by 4 meter = New breadth is y+4

Area of the rectangle is increased by 89 m2 = (x * y) + 89.

hence, the equation becomes

xy + 89 = (x -1)(y + 4)

4x – y – 93 = 0 —————–(ii)

Now by solving equation (i) and (ii) we get,

x = 224/8 = 28

y = 152/8 = 19

Therefore, the length of rectangle is 28 m and the breadth of rectangle is 19 m.

问题4. X和Y的收入之比为8：7，其支出的比率为19:16。如果每个人都节省₹1250，则找到他们的收入。

解决方案：

Let the income be denoted by x and the expenditure be denoted by y respectively.

Given that,

The income of X is ₹ 8x and the expenditure of X is 19y.

The income of Y is ₹ 7x and the expenditure of Y is 16y.

So, by calculating the savings, we get

Saving of X = 8x – 19y = 1250

Saving of Y = 7x – 16y = 1250

Hence, the equations are:

8x – 19y – 1250 = 0 —————-(i)

7x – 16y – 1250 = 0 —————(ii)

Now by solving equation (i) and (ii) we get,

x = 3750/5 = 750

If, x = 750, then

The income of X = 8x

= 8 x 750 = 6000

The income of Y = 7x

= 7 x 750 = 5250

Therefore, the income of X is ₹ 6000 and the income of Y is ₹ 5250

问题5. A和B都有钱。如果A给B ￥₹30，那么B剩下的钱是A的两倍。但是，如果B给B ￥₹10，那么A的钱将是B的三倍。每个钱有多少?

解决方案：

Let’s assume the money with “A” be ₹ x and the money with “B” be ₹ y.

Given that,

Case 1:

If A gives ₹ 30 to B, then B will have twice the money left with A.

According to the case the equation becomes,

y + 30 = 2(x – 30)

y + 30 = 2x – 60

2x – y – 60 – 30 = 0

2x – y – 90 = 0 —————(i)

Case 2:

If B gives ₹ 10 to A, then A will have thrice as much as is left with B.

According to the case the equation becomes,

x + 10 = 3(y – 10)

x + 10 = 3y – 10

x – 3y + 10 + 30 = 0

x – 3y + 40 = 0 —————(ii)

On multiplying equation (ii) with 2, we get,

2x – 6y + 80 = 0

Subtract equation (ii) from (i), we get,

2x – y – 90 – (2x – 6y + 80) = 0

5y – 170 =0

y = 34

Now, put the value y = 34 in equation (i), and we get,

x = 62

Hence, the money with A is ₹ 62 and the money with B be ₹ 34

问题6. ABCD是一个循环的四边形，使得∠A=(4y + 20)°，∠B=(3y – 5)°，∠C=(+ 4x)°，∠D=(7x + 5)°。找到四个角度。 [NCERT]

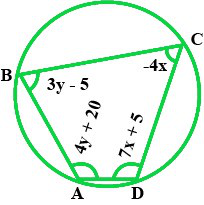
解决方案：

Given that,

∠A = 4y + 20,

∠B = 3y-5,

∠C = – 4x,

∠D = 7x+5.

As we know that opposite angles of a cyclic quadrilateral are supplementary,

∠A + ∠C = 180°

4y+20-4x = 180

-4x+4y = 160

(-x + y) = 40 ——————-(i)

and,

∠B+∠D = 180°

3y-5+7x+5 = 180

7x+3y = 180 —————-(ii)

-7x+7y = 280 (multiplying eqⁿ (i) by 7 and we get)

10y = 460

y = 46

put the value of y in eqⁿ (i) and we get,

-x+46 = 40

-x = -6 = 6

Hence the value of x = 6 and y = 46.

问题7：2个男人和7个男孩可以在4天内完成一项工作。 4名男子和4名男孩在3天内完成了相同的工作。一个男人和一个男孩要花多长时间?

解决方案：

Let’s assume that the time required for a man alone to finish the work be “x” days and also the time required for a boy alone to finish the work be “y” days.

The work done by a man in one day = 1/x

The work done by a boy in one day = 1/y

Similarly,

The work done by 2 men in one day = 2/x

The work done by 7 boys in one day = 7/y

therefore according to the condition given in question,

2 men and 7 boys together can finish the work in 4 days

4(2/x + 7/y) = 1

8/x + 28/y = 1 ——————-(i)

And, the second condition from the question states that,

4 men and 4 boys can finish the work in 3 days

3(4/x + 4/y) = 1

12/x + 12/y = 1 —————-(ii)

Now by solving equation (i) and (ii) we get,

put, 1/x = u and 1/y = v

therefore, the equations (i) and (ii) becomes,

8u + 28v = 1

12u + 12v = 1

8u + 28v – 1 = 0 —————-(iii)

12u + 12v – 1 = 0 —————-(iv)

Now by solving equation (iii) and (iv) we get,

u = 1/15

1/x = 1/15

x = 15

and,

v = 1/60

1/y = 1/60

y = 60

Therefore, the time required for a man alone to finish the work is 15 days and the time required for a boy alone to finish the work is 60 days.

问题8.在ΔABC中，∠A= x ^o ，∠B=(3x – 2) ^o ，∠C= y ^o 。同样，∠C–∠B= 9 ^o 。找到三个角度。

解决方案：

Given that,

∠A = x^o,

∠B = (3x – 2)^o,

∠C = y^o,

∠C – ∠B = 9^o

∠C = 9^∘ + ∠B

∠C = 9 + 3x − 2

∠C = 7^o + 3x^o

Substituting the value for

∠C = y^o in above equation we get,

yo = 7^o + 3x^o

As we know that, ∠A + ∠B + ∠C = 180^o (Angle sum property of a triangle)

= x^o + (3x^∘ − 2^∘) + (7^∘ + 3x^∘) = 180^∘

= 7x^∘ + 5^∘ = 180^∘

= 7x^∘ = 175^∘

= x = 25^∘

Hence, calculating for the individual angles we get,

∠A = x^o = 25^o

∠B = (3x – 2)^o = 73^o

∠C = (7 + 3x)^o = 82°

Hence, ∠A = 25^o, ∠B = 73^o and ∠C = 82^o.

问题9.在循环四边形ABCD中，∠A=(2x + 4) ^o ，，B =(y + 3) ^o ，∠C=(2y + 10) ^o ，∠D=(4x – 5) ^o 。找到四个角度。

解决方案：

As we know that,

The sum of the opposite angles of cyclic quadrilateral should be 180o.

And, in the cyclic quadrilateral ABCD,

Angles ∠A and ∠C & angles ∠B and ∠D are the pairs of opposite angles.

therefore,

∠A + ∠C = 180^o and

∠B + ∠D = 180^o

Substituting the values given to the above two equations, we have

For ∠A + ∠C = 180^o

= ∠A = (2x + 4)^o and ∠C = (2y + 10)^o

2x + 4 + 2y + 10 = 180^o

2x + 2y + 14 = 180^o

2x + 2y = 180^o – 14^o

2x + 2y = 166 —————(i)

And for, ∠B + ∠D = 180^o, we have

= ∠B = (y+3)o and ∠D = (4x – 5)o

y + 3 + 4x – 5 = 180^o

4x + y – 5 + 3 = 180

4x + y – 2 = 180

4x + y = 180 + 2

4x + y = 182^o ——————-(ii)

Now for solving (i) and (ii), we perform

Multiplying equation (ii) by 2 to get,

8x + 2y = 364 ———–(iii)

And now, subtract equation (iii) from (i) and we get,

-6x = -198

x = −198/ −6 = 33

Now, substituting the value of x = 33o in equation (ii) and we get,

4x + y = 182

132 + y = 182

y = 182 – 132 = 50

Thus, calculating the angles of a cyclic quadrilateral and we get,

∠A = 2x + 4 = 66 + 4 = 70^o

∠B = y + 3 = 50 + 3 = 53^o

∠C = 2y + 10 = 100 + 10 = 110^o

∠D = 4x – 5 = 132 – 5 = 127^o

Therefore, the angles of the cyclic quadrilateral ABCD are

∠A = 70^o, ∠B = 53^o, ∠C = 110^o and ∠D = 127^o

问题10：Yash在测试中获得40分，每个正确答案获得3分，而每个错误答案获得1分。如果每个正确答案被授予4分，而每个错误答案被扣除2分，那么Yash将获得50分。测试中有多少个问题?

解决方案：

Let’s assume that the total number of correct answers be x and the total number of incorrect answers be y.

Hence, their sum will give the total number of questions in the test i.e. x + y

Given that,

Case 1: When 3 marks is awarded for every right answer and 1 mark deducted for every wrong answer.

According to this type, the total marks scored by Yash is 40. (Given)

therefore, the equation will be

3x – 1y = 40 —————–(i)

Case 2: When 4 marks is awarded for every right answer and 2 marks deducted for every wrong answer.

According to this, the total marks scored by Yash is 50. (Given)

therefore, the equation will be

4x – 2y = 50 ————–(ii)

Thus, by solving (i) and (ii) we obtained the values of x and y.

From (i), we get

y = 3x – 40 ————–(iii)

put this value of y in (ii) and we get,

4x – 2(3x – 40) = 50

4x – 6x + 80 = 50

2x = 30

x = 15

Putting x = 14 in (iii) and we get,

y = 3(15) – 40 = 5

therefore, x + y = 15 + 5 = 20

Therefore, the number of questions in the test were 20.

问题11：在ΔABC中，∠A= x ^o ，∠B= 3x ^o ，∠C= y ^o 。如果3y – 5x = 30，则证明三角形是直角的。

解决方案：

We need to prove that ΔABC is right angled.

Given that,

∠A = x^o, ∠B = 3x^o and ∠C = y^o

As we know that,

Sum of the three angles in a triangle is 180o (Angle sum property of a triangle)

∠A + ∠B + ∠C = 180^o

x + 3x + y = 180

4x + y = 180 —————-(i)

3y – 5x = 30 ————-(ii) (Given)

To solve (i) and (ii),

Multiplying equation (i) by 3 and we get,

12x + 36y = 540 ————-(iii)

Now, subtracting equation (ii) from equation (iii) and we get,

17x = 510

x = 510/17 = 30

Substituting the value of x = 30o in equation (i) and we get,

4x + y = 180

120 + y = 180

y = 180 – 120 = 60

Thus the angles ∠A, ∠B and ∠C are calculated to be

∠A = xo = 30^o

∠B = 3xo = 90^o

∠C = yo = 60^o

A right angled triangle is a triangle with any one side right angled to other, i.e., 90^o to other.

and here we have ∠B = 90^o.

Therefore, the triangle ABC is right angled. Hence, proved.

问题12.在城市中的租车费用包括固定费用以及所覆盖距离的费用。对于12公里的旅程，需支付₹89，对于20公里的旅程，则需支付₹145。一个人行驶30公里，需要支付什么费用?

解决方案：

Let the fixed charge of the car be ₹ x and,

Let the variable charges of the car be ₹ y per km.

therefore the equations become,

x + 12y = 89 ————–(i)

x + 20y = 145 ————–(ii)

Now, by solving (i) and (ii) we can find the charges.

Subtract (i) from (ii) and we get,

-8y = -56

y = −56 − 8 = 7

now, substitute the value of y in equation (i) and we get,

x + 12y = 89

x + 84 = 89

x = 89 – 84 = 5

Thus, the total charges for travelling a distance of 30 km can be calculated as: x + 30y

x + 30y = 5 + 210 = ₹ 215

Therefore, a person has to pay ₹ 215 for travelling a distance of 30 km by the car.