问题1.找到GP 5 / 2、5 / 4、5 / 8,…的第20和第n个项
解决方案:
According to the question
G.P: 5/2, 5/4, 5/8, …
So, first term(a) = 5/2
So, the common ratio(r) = 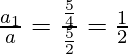
Find: 20th and nth terms of the given G.P
So, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
Now we find the 20th terms of the given G.P:
a20 = (5/2)(1/2)20-1 = (5/2)(1/2)19= ![]()
Find the nth terms of the given G.P:
an = ![]()
问题2。找到GP的第12个项,其第8个项是192,共同比率是2。
解决方案:
According to the question
Common ration(r) = 2
and 8th term is 192
So let us considered a be the first term
So,
a8 = ar7
ar7 = 192
a(2)7 = 192
a = 3/2
Find: 12th term of a G.P.
As we know that the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio
So, we find 12th term of a G.P.
a12 = ar12 – 1
a12 = ar11
a12 = (3/2)(2)11
a12 = 3072
问题3,第5,第8和第11一个GP的术语是分别为p,q和s。证明q 2 = ps。
解决方案:
According to the question
The 5th, 8th and 11th terms of a G.P. are p, q and s
Prove: q2 = ps
Proof:
Let a G.P. with first term a and common ratio r,
So, a5 = ar4 = p ….(1)
a8 = ar7= q ….(2)
a11 = ar10 = s ….(3)
Now divide eq(2) by (1), we get
ar7/ar4 = q/p
r3 = q/p ….(4)
Now divide eq(3) by (2), we get
ar10/ar7= s/q
r3 = s/q ….(5)
From eq(4) and (5), we get
q/p = s/q
q2 = ps
Hence Proved
问题4.一个GP的第4项是正方形其第二项的和的第一项是- (3)确定的第7次项。
解决方案:
According to the question
First term(a) = – 3
and the 4th term of a G.P. is square of its second term
Find: 7th term
Let us considered r be the common ratio
As we know that the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio
So, a4 = ar3
It is given that the 4th term of a G.P. is square of its second term
a4 = (a2)2
ar3 = (a2)2
ar3 = (ar)2
ar3 = a2r2
r = a
Now put the value of a, we get
r = -3
Now, we find the 7th term
a7 = ar7 – 1
a7 = ar6
= −3 x (−3)6 =−2187
问题5.以下序列中的哪个术语:
(a)2、2√2、4,…是128吗?
解决方案:
According to the question
G.P.: 2, 2√2, 4, …
So, first term(a) = 2
So, the common ratio(r) = √2
As we know that, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
128 = 2(√2)n – 1
(2)7 = 2(√2)n – 1
(2)7 = 2((2)1/2)n – 1
(2)7 = 2(2)(n – 1)/2
(2)6 = (2)(n – 1)/2
6 = (n – 1)/2
12 = n – 1
12 + 1 = n
n = 13
Hence, the 13th term of the G.P. is 128
(b)√3,3,3√3,…。是729吗?
解决方案:
According to the question
G.P.: √3, 3, 3√3, ….
So, first term(a) = √3
So, the common ratio(r) = √3
As we know that, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
729 = √3(√3)n-1
(3)6 = √3(√3)n-1
(3)6 = (3)1/2((3)1/2)n-1
(3)6 = (3)1/2(3)n-1/2
(3)6 = (3)1/2+(n-1)/2
6 = 1/2 + (n – 1)/2
6 – 1/2 = (n – 1)/2
(12 – 1)/2 = (n – 1)/2
11 = n – 1
n = 12
Hence, the 12th term of the G.P. is 729
(C) 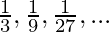 是
是 ?
?
解决方案:
According to the question
G.P.: ![]()
So, first term(a) = 1/3
So, the common ratio(r) = 1/3
As we know that, the nth term of G.P can be expressed using formula:
an = arn – 1
Where a is 1st term and r is the common ratio.
![]()
(1/3)9 = (1/3)n
n = 9
Hence, the 9th term of the G.P. is 1/19683
问题6.对于x的什么值,数字-2 / 7,x。 -7 / 2…在GP中吗?
解决方案:
According to the question
Numbers are -2/7, x. -7/2…
The common ration is (r) = ![]() = -7x/2
= -7x/2
Again the common ration(r) = = ![]() = -7/2x
= -7/2x
So,
-7x/2 = -7/2x
7x/2 = 2/7x
14x2 = 14
x2 = 14/14
x = ±1
在练习7到10中的每个几何级数中找到表示的项数之和:
问题7. 0.15、0.015、0.0015,…20个字词。
解决方案:
According to the question
G.P.: 0.15, 0.015, 0.0015, …
So, first term(a) = 0.15
So, the common ratio(r) = 0.1
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
So, S20 = (0.15)[(1 – (0.1)20)/(1 – 0.1)]
= (0.15/0.9)(1 – (0.1)20)
= 1/6(1 – (0.1)20)
问题8:7√,√21,3√7,… n项。
解决方案:
According to the question
G.P.: √7, √21, 3√7,…
So, first term(a) = √7
So, the common ratio(r) = √3
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
So, Sn = (√7)[(1 – (√3)n)/(1 – √3)]
= (√7)[(1 – (√3)n)/(1 – √3)] x [(1 + √3)/(1 + √3)]
= -(√7)(1 + √3)/2(1 – (3)n/2)
= (√7)(1 + √3)/2((3)n/2 – 1)
问题9. 1,-a,a 2 ,-a 3 ,… n项(如果≠– 1)。
解决方案:
According to the question
G.P.: 1, -a, a2, -a3,…
So, first term(a) = 1
So, the common ratio(r) = -a
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
So, ![]()
问题10. x 3 ,x 5 ,x 7 ,…n个项(如果x≠±1)。
解决方案:
According to the question
G.P.: x3, x5, x7, …
So, first term(a) = x3
So, the common ratio(r) = x2
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
So,
![]()
![]()
问题11:评估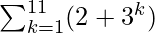
解决方案:
![]() = (2 + 31) + (2 + 32) + (2 + 33) + …. + (2 + 311)
= (2 + 31) + (2 + 32) + (2 + 33) + …. + (2 + 311)
= (2 + 2 + …11 terms) + (3 + 32 + 33+…11 terms)
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
So, Sn = 2 x 11 + 3(311 – 1)/3 – 1
Sn = 22 + 3/2((311 – 1))
问题12. GP的前三个项的总和为39/10,其乘积为1。找到共同比率和项。
解决方案:
Let us considered the three terms a/r, a, ar of the G.P.
According to the question
![]() = 1
= 1
a3 = 1
a = 1
Also.
![]()
Now put the value of a, we get
![]()
![]()
10r2 + 10r + 10 = 39r
10r2 – 29r + 10 = 0
On solving the equation, we get
r = 2/5, 5/2
So, the G.P. is 5/2, 1, 2/5.
问题13 GP 3的多少而言,3 2,3 3,…都需要给总和120?
解决方案:
According to the question
G.P.: 3, 32, 33, …
So, first term(a) = 3
So, the common ratio(r) = 3
Sn = 120
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
Sn = (3)(1 – (3)n)(1-3)
120 = (3)(1 – (3)n)
-240 = (3)(1 – (3)n)
-80 = 1 – (3)n
-80 – 1 = – (3)n
-81 = – (3)n
(3)4 = (3)n
n = 4
Hence, 4 terms of G.P. are needed to give the sum 120
问题14. GP的前三个项的总和是16,接下来的三个项的总和是128。确定GP的第一个项,公共比率和n个项的总和
解决方案:
Let us considered the first three terms of the G.P. are a, ar, ar2 and
first term of G.P. be a and common ratio r.
Find: the first term, the common ratio, and the sum to n terms of the G.P.
According to the question
a + ar + ar2 = 16
a(1 + r + r2) = 16 …….(1)
ar3 + ar4 + ar5 = 128
ar3(1 + r + r2) = 128 …….(2)
Now divide eq(2) by (1), we get
ar3(1 + r + r2)/ a(1 + r + r2) = 128/16
r3 = 8
r = 2
Now put the value of r in eq(1), we get
a(1 + (2) + (2)2) = 16
a(1 + 2 + 4) = 16
a(7) = 16
a = 16/7
Now we find the sum to n terms of the G.P.
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
![]()
问题15.给定一个GP = 729和第7项64的GP,确定S 7 。
解决方案:
According to the question
The first term(a) = 729
and 7th term 64
Find: S7
Let the common ratio be r.
a7 = ar6 = 64
r6 = 64/729
r = ±2/3
Now we find the sum to 7th terms of the G.P.
As we know that, the sum of n terms of G.P. with 1st term a & common ratio r is given by
![]()
On taking r = +2/3
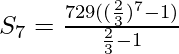 = 2059
= 2059
On taking r = -2/3
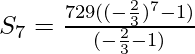 = 463
= 463
问题16。找到一个GP,其前两项之和为– 4,而第五项为第三项的4倍。
解决方案:
Let the first term of the G.P. be a and common ratio be r.
According to the question
a + ar = -4
a5 = 4(a3)
So, ar4 = 4(ar2)
r2 = 4
r = ±2
When r = +2 then
a + ar = a + 2a = 3a = −4
a = -4/3
Then the G.P. is ![]()
When r = -2 then
a + ar = a − 2a = −a = −4
a = 4
Then the G.P. is 4, -8, 16, -32,…