问题1.在标准形式a + ib中表示以下复数:
(i)(1 + i)(1 + 2i)
解决方案:
We have, z = (1 + i) (1 + 2i)
= 1 (1 + 2i) + i (1 + 2i)
= 1 + 2i + i + 2i2
= 1 + 3i + 2(−1)
= 1 + 3i − 2
= −1 + 3i
Therefore, the standard form is −1 + 3i where a = −1 and b = 3.
(ii) 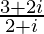
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = −4/5 and b = −7/5.
where a = −4/5 and b = −7/5.
(iii) 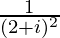
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = 3/25 and b = −4/25.
where a = 3/25 and b = −4/25.
(iv) 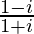
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
= −i
Therefore, the standard form is −i where a = 0 and b = −1.
(v) 
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = 37/13 and b = 16/13.
where a = 37/13 and b = 16/13.
(六) 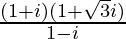
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
= –√3 + i
Therefore, the standard form is –√3 + i where a = –√3 and b = 1.
(vii) 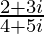
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = 23/41 and b = 2/41.
where a = 23/41 and b = 2/41.
(viii) 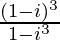
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
= –3 – i
Therefore, the standard form is –3 – i where a = –3 and b = – 1.
(ix)(1 + 2i) -3
解决方案:
We have z = (1 + 2i)-3
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = –3/13 and b = 2/13.
where a = –3/13 and b = 2/13.
(X) 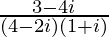
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = –1/4 and b = –3/4.
where a = –1/4 and b = –3/4.
(xi) 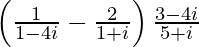
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the standard form is![]() where a = 478/884 and b = 928/884.
where a = 478/884 and b = 928/884.
(xii) 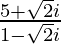
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
= 1+ 2√2i
Therefore, the standard form is 1+ 2√2i where a = 1 and b = 2√2.
问题2。找到x和y的实值,如果
(i)(x + iy)(2 – 3i)= 4 + i
解决方案:
We have,
=> (x + iy) (2 – 3i) = 4 + i
=> 2x – 3xi + 2yi – 3yi2 = 4 + i
=> 2x + (–3x+2y)i + 3y = 4 + i
=> (2x+3y) + i(–3x+2y) = 4 + i
On comparing real and imaginary parts on both sides, we get,
2x + 3y = 4 . . . . (1)
And –3x + 2y = 1 . . . . (2)
On multiplying (1) by 3 and (2) by 2 and adding, we get
=> 6x – 6x – 9y + 4y = 12 + 2
=> 13y = 14
=> y = 14/13
On putting y = 14/13 in (1), we get
=> 2x + 3(14/13) = 4
=> 2x = 4 – (42/13)
=> 2x = 10/13
=> x = 5/13
Therefore, the real values of x and y are 5/13 and 14/13 respectively.
(ii)(3x – 2iy)(2 + i) 2 = 10(1 + i)
解决方案:
We have,
=> (3x – 2iy) (2 + i)2 = 10(1 + i)
=> (3x – 2yi) (4 + i2 + 4i) = 10 + 10i
=> (3x – 2yi) (3 + 4i) = 10+10i
=> 3x – 2yi =![]()
=> 3x – 2yi =![]()
=> 3x – 2yi =![]()
=> 3x – 2yi =![]()
On comparing real and imaginary parts on both sides, we get,
=> 3x = 70/25 and –2y = –10/25
=> x = 70/75 and y = 1/5
Therefore, the real values of x and y are 70/75 and 1/5 respectively.
(iii) 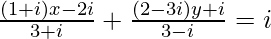
解决方案:
We have,
=>![]()
=>![]()
=>![]()
=> (4+2i) x − 3i − 3 + (9−7i)y = 10i
=> (4x+9y−3) + i(2x−7y−3) = 10i
On comparing real and imaginary parts on both sides, we get,
4x + 9y − 3 = 0 . . . . (1)
And 2x − 7y − 3 = 10 . . . . (2)
On multiplying (1) by 7 and (2) by 9 and adding, we get,
=> 28x + 18x + 63y – 63y = 117 + 21
=> 46x = 117 + 21
=> 46x = 138
=> x = 3
On putting x = 3 in (1), we get
=> 4x + 9y − 3 = 0
=> 9y = −9
=> y = −1
Therefore, the real values of x and y are 3 and −1 respectively.
(iv)(1 + i)(x + iy)= 2 – 5i
解决方案:
We have,
=> (1 + i) (x + iy) = 2 – 5i
=> x + iy =![]()
=> x + iy =![]()
=> x + iy =![]()
=> x + iy =![]()
On comparing real and imaginary parts on both sides, we get,
=> x = −3/2 and y = −7/2
Therefore, the real values of x and y are −3/2 and −7/2 respectively.
问题3.查找以下复数的共轭:
(i)4 – 5i
解决方案:
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of (4 – 5i) is (4 + 5i).
(ii) 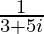
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of![]() is
is![]() .
.
(iii) 
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of![]() is
is![]() .
.
(iv) 
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
= 2 – 4i
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of![]() is 2 + 4i.
is 2 + 4i.
(v) 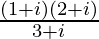
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
We know the conjugate of a complex number (a + ib) is (a – ib).
The conjugate of![]() is
is![]() .
.
(六) 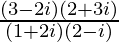
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
We know the conjugate of a complex number (a + ib) is (a – ib).
Therefore, the conjugate of![]() is
is![]() .
.
问题4.找到以下复数的乘法逆:
(i)1 – i
解决方案:
We have z = 1 – i
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=![]()
=![]()
=![]()
=![]()
Therefore, the multiplicative inverse of (1 – i) is![]() .
.
(ii)(1 +我√3) 2
解决方案:
We have, z = (1 + i √3)2
= 1 + 3i2 + 2 i√3
= 1 + 3(−1) + 2 i√3
= 1 – 3 + 2 i√3
= −2 + 2 i√3
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, the multiplicative inverse of (1 + i √3)2 is![]() .
.
(iii)4 – 3i
解决方案:
We have z = 4 – 3i
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=![]()
=![]()
=![]()
=![]()
Therefore, the multiplicative inverse of 4 – 3i is![]() .
.
(iv)√5+ 3i
解决方案:
We have z = √5 + 3i
We know the multiplicative inverse of a complex number z is 1/z. So, we get,
=![]()
=![]()
=![]()
=![]()
Therefore, the multiplicative inverse of √5 + 3i is![]() .
.
问题5.如果z 1 = 2 − i,z 2 = 1 + i,则找到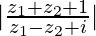 。
。
解决方案:
Given z1 = 2 − i, z2 = 1 + i, we get,
![]() =
=![]()
=![]()
=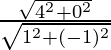
=![]()
= 2√2
Therefore, the value of![]() is 2√2.
is 2√2.
问题6。如果z 1 =(2 – i),z 2 =(–2 + i),则找到
(i)重新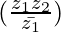
解决方案:
Given z1 = (2 – i), z2 = (–2 + i), we get,
![]() =
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, Re![]() =
=![]() .
.
(ii)我
Now,![]() =
=![]()
=![]()
=![]()
=![]()
=![]()
Therefore, Im![]() = 0.
= 0.
问题7.求出模数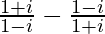 。
。
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
= 2i
So, modulus of z =![]() = 2.
= 2.
Therefore, the modulus of![]() is 2.
is 2.
问题8.如果x + iy =  ,证明x 2 + y 2 = 1。
,证明x 2 + y 2 = 1。
解决方案:
We have,
=> x + iy =![]()
On applying modulus on both sides we get,
=> |x + iy| =![]()
=> |x + iy| =![]()
=>![]()
=>![]() = 1
= 1
=> x2 + y2 = 1
Hence proved.
问题9.求n的最小正整数值![由QuickLaTeX.com渲染 \left[\frac{1+i}{1-i}\right]^n](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2013%20Complex%20Numbers%20%E2%80%93%20Exercise%2013.2%20%7C%20Set%201_196.jpg) 是真实的。
是真实的。
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
= in
For n = 2, we have in = i2 = −1, which is real
Therefore, the least positive integral value of n for which![]() is real is 2.
is real is 2.
问题10.求出复数θ的实值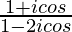 是纯粹的真实。
是纯粹的真实。
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
For a complex number to be purely real, the imaginary part should be equal to zero.
So, we get,![]() = 0
= 0
=> cos θ = 0
=> cos θ = cos π/2
=> 2nπ ± π/2, for n ∈ Z
Therefore, the values of θ for the complex number to be purely real are 2nπ ± π/2, for n ∈ Z.
问题11.求n的最小正整数值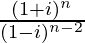 是一个实数。
是一个实数。
解决方案:
We have, z =![]()
=![]()
=![]()
=![]()
=![]()
=![]()
=![]()
= in × (−2i)
= −2in+1
For n = 1, we have z = −2i1+1
= −2i2
= 2, which is real
Therefore, the smallest positive integer value of n for which is a real number![]() is 1.
is 1.
问题12。 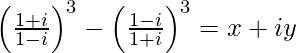 ,找到(x,y)。
,找到(x,y)。
解决方案:
We have,
=>![Rendered by QuickLaTeX.com \left[\frac{(1+i)^2}{(1-i)(1+i)}\right]^3-\left[\frac{(1-i)^2}{(1+i)(1-i)}\right]^3=x+iy](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2013%20Complex%20Numbers%20%E2%80%93%20Exercise%2013.2%20%7C%20Set%201_219.jpg)
=>![Rendered by QuickLaTeX.com \left[\frac{1+i^2+2i}{1-i^2}\right]^3-\left[\frac{1+i^2-2i}{1-i^2}\right]^3=x+iy](https://mangdo-1254073825.cos.ap-chengdu.myqcloud.com//front_eng_imgs/geeksforgeeks2021/Class%2011%20RD%20Sharma%20Solutions%20%E2%80%93%20Chapter%2013%20Complex%20Numbers%20%E2%80%93%20Exercise%2013.2%20%7C%20Set%201_220.jpg)
=>![]()
=> i3 – (–i3) = x + iy
=> 2i3 = x + iy
=> x + iy = −2i
On comparing real and imaginary parts on both sides, we get,
=> (x, y) = (0, −2)
问题13 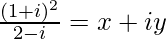 ,找到x + y。
,找到x + y。
解决方案:
We have,
=>![]()
=>![]()
=>![]()
=>![]()
=>![]()
On comparing real and imaginary parts on both sides, we get,
=> x = −2/5 and y = 4/5
So, x + y = −2/5 + 4/5
= (−2+4)/5
= 2/5
Therefore, the value of (x + y) is 2/5.