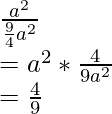第10类RD Sharma解决方案–第13章概率–练习13.2

问题1.假设您在图2所示的矩形区域上随机放置一条领带。以下。它将落入直径为1 m的圆内的概率是多少?

解决方案：

Area of a circle with the specified radius 0.5 m = (0.5)² = 0.25 πm²

Area of the rectangle = length × breadth = 3 × 2 = 6m²

$Probability = \frac{measure of specified region}{measure of whole region}$

Now,

The probability that the tie will land inside the circle, = area of circle/area of rectangle 

= 0.25 π m² / 6 m²

= π /24 

Therefore, the probability that the tie will land inside the circle = π/24

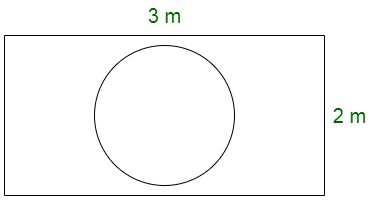
问题2。在附图中，一个漂亮的微调器放置在圆的中心O处。直径AOB和半径OC将圆分成标记为X，Y和Z的三个区域。如果∠BOC= 45°。微调器将降落在区域X中的概率是多少?

解决方案：

Given,

∠BOC = 45°

Also, by the application of linear pair

∠AOC = 180 – 45 = 135° 

Area of circle of radius r = πr²

Area of region x according to the figure= θ/360 × πr²

= 135/360 × πr²

= 3/8 × πr²

$x = \frac{area of x}{area of circle} \\ x = \frac{\frac{3}{8}\pi r^2}{\pi r^2} \\ x = \frac{3}{8}$

Hence, The required probability that the spinner will land in the region X is 3/8.

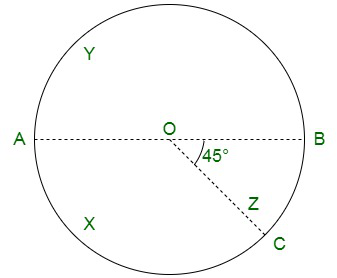
问题3。目标如图2所示。下面的三个同心圆半径分别为3、7和9 cm。dart被抛出并落在目标上。dart落在阴影区域上的概率是多少?

解决方案：

Now, we have the following values

I circle – with radius 3

II circle – with radius 7

III circle – with radius 9

Their corresponding areas are : 

Area of I circle = π(3)² = 9π

Area of II circle = π(7)² = 49π

Area of III circle = π(9)² = 81π

Now, calculating, 

Area of shaded region = Area of II circle – Area of I circle

= 49π − 9π

= 40π

Now, the probability that it will land on the shaded region is given by,

$\frac{area of shaded region}{area of third circle} \\ = \frac{40\pi}{81 \pi} \\ = \frac{40}{81}$

Hence, the required probability that the dart will land on the shaded region is equivalent to 40/81.

问题4。在图中，点A，B，C和D是四个圆的中心，每个圆的半径为一个单位。如果从内部正方形ABCD中随机选择一个点。从阴影区域中选择该点的概率是多少?

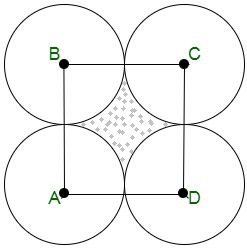
解决方案：

Radius of each of the circles = 1 unit 

Therefore, 

side of the square ABCD = 2 units

Area of sq ABCD = side²  = a² = 2 * 2 = 4 sq. units

Also,

Area of four quadrants at A,B,C and D is given by

= 4 * 1/4 πr²  

Substituting the values of r , we get, 

= π sq. unit

Therefore, area of shaded region = (4 – π) sq. units

And, the probability of the point that is selected from the shaded region = (4 – π)/4 = (1 – π/4)

问题5.在图中，JKLM是一个边长为6个单位的正方形。点A和B分别是边KL和LM的中点。如果从正方形内部随机选择一个点。从∆JAB内部选择该点的概率是多少?

解决方案：

We know,

Length of sq side of JKLM = 6 units

Now, the area of the sq. JKLM = 6²  = 36 sq. units

We have, A and B as the midpoints of sides KL and LM.

Now, 

AL = AK = BM = BL = 3 units

Therefore, 

Area of triangle AJK = (JK * AK) /2 = (6 * 3) / 2 = 9 sq. units

Area of triangle JMB = (JM * MB) /2 = (6 * 3) / 2 = 9 sq. units

Area of triangle LAB = (LA * LB) /2 = (3 * 3) / 2 = 9/2 sq. units

Sum of these areas = 9 + 9 + 9/2 = 45/2 sq units.

Area of triangle JAB = Area of sq JKLM – Area of all the three triangles 

= 36 – 45/2 = 72-45/2 sq. units 

= 27/2 sq. units  

Probability = Area of triangle JAB/ Area of sq JMLK 

= 27 /(2 * 36) = 3/8

问题6.在图中，显示了方形dart板。大正方形的边的长度是小正方形的边的长度的1.5倍。如果掷dart并落在较大的正方形上。它降落在较小正方形内部的概率是多少?

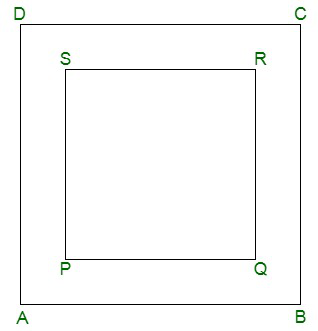
解决方案：

Let us assume the side of the smaller sq to be a. 

Also, let the length of the side of sq ABCD be 3/2 * a

Area of the sq. ABCD = (3a/2)² = 9/4 a² sq. units

Therefore, 

Probability = $\frac{a^2}{\frac{9}{4}a^2} \\ = a^2 * \frac{4}{9a^2} \\ = \frac{4}{9}$