第 12 类 RD Sharma 解决方案 - 第 31 章概率 - 练习 31.7 |设置 3

问题 27. 有三个硬币。一种是双头硬币，另一种是 75% 的正面朝上的有偏硬币，第三种是无偏硬币。三枚硬币中的一枚被随机选择并投掷，它显示正面。它是两面硬币的概率是多少？

解决方案：

Let us assume that the events are

E₁ = choosing a two-headed coin

E₂ = choosing a biased coin 

E₃ = choosing an unbiased coin

A = the coin shows heads.

So, 

P(E₁) = 1/3

P(E₂) = 1/3

P(E₃) = 1/3

Now,

P(A/E₁) = 1

P(A/E₂) = 75% = 3/4

P(A/E₃) = 1/2

By using Bayes’ theorem, the required probability is 

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{1}{3} \times 1}{\frac{1}{3} \times 1 + \frac{1}{3} \times \frac{3}{4} + \frac{1}{3} \times \frac{1}{2}}$

= 4/9

问题 28。假设患者心脏病发作的几率为 40%。还假设冥想和瑜伽课程可将心脏病发作的风险降低 30%，某些药物的处方可将其风险降低 25%。一次，患者可以以相等的概率选择两个选项中的任何一个。假设在经历了两个选项之一后，随机选择的患者心脏病发作。找出患者遵循冥想和瑜伽课程的概率？

解决方案：

Let us assume that the events are

E₁ = follow the course of yoga and meditation

E₂ = follow the drug prescriptions

A = the selected person had heart attacak

So, 

P(E₁) = 1/2

P(E₂) = 1/2

Now,

P(A/E₁) = 0.4 x 0.70 = 0.28

P(A/E₂) = 0.4 x 0.75 = 0.30

By using Bayes’ theorem, the required probability is 

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{1}{2} \times 0.28}{\frac{1}{2} \times 0.28 + \frac{1}{2} \times 0.30}$

= 14/29

问题 29. 彩球分布在四个盒子中，如下表所示：

Box	Colour
	Black	White	Red	Blue
I	3	4	5	6
II	2	2	2	2
III	1	2	3	1
IV	4	3	1	5

随机选择一个盒子，然后从选定的盒子中随机抽取一个球。球的颜色是黑色，抽出的球是来自盒子 III 的概率是多少。

解决方案：

Let us assume that the events are

A = the ball is black

E₁ = box I selected

E₂ = box II selected

E₃ = box III is selected 

E₄ = box IV is selected

So, 

P(E₁) = 1/4

P(E2) = 1/4

P(E₃) = 1/4

P(E₄) = 1/4

Now,

P(A/E₁) = 3/18

P(A/E₂) = 2/8

P(A/E₃) = 1/7

P(A/E₄) = 4/13

By using Bayes’ theorem, the required probability is 

P(E₃/A) = $\frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)+P\left( E_3 \right)P\left( A/ E_3 \right)+P\left( E_4 \right)P\left( A/ E_4 \right)}$

= $\frac{\frac{1}{4} \times \frac{1}{7}}{\frac{1}{4} \times \frac{3}{18} + \frac{1}{4} \times \frac{2}{8} + \frac{1}{4} \times \frac{1}{7} + \frac{1}{4} \times \frac{4}{13}}$

= $\frac{\frac{1}{7}}{\frac{1}{6} + \frac{1}{4} + \frac{1}{7} + \frac{4}{13}}$

= 156/947

问题 30. 如果一台机器设置正确，它可以生产 90% 的合格产品。如果设置不正确，它只会产生 40% 的可接受项目。过去的经验表明，80% 的设置都是正确完成的。如果经过一定的设置，机器产生了 2 个可接受的项目，求机器设置正确的概率。

解决方案：

Let us assume that the events are

A = the machine produces two acceptable items.

E₁ = the machine is correctly set up 

E₂ = the machine is incorrectly set up

So, 

P(E₁) = 0.8

P(E₂) = 0.2

Now,

P(A/E₁) = 0.9 (0.9) = 0.81

P(A/E₂) = 0.40 (0.40) = 0.16

By using Bayes’ theorem, the required probability is 

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{0 . 8 \times 0 . 81}{0 . 8 \times 0 . 81 + 0 . 2 \times 0 . 16}$

= 81/85

问题 31. 袋子 A 包含 3 个红色和 5 个黑色球，而袋子 B 包含 4 个红色和 4 个黑色球。两个球从袋子 A 中随机转移到袋子 B 中，然后从袋子 B 中随机抽取一个球。如果发现从袋子 B 中抽出的球是红球，求两个红球从 A 转移到 B 的概率。

解决方案：

According to the question, bag A contains 3 red and 5 black balls and bag B contains 4 red and 4 black balls.

Let us assume that the events are

E₁ = Two red balls are transferred from bag A to bag B.

E₂ = One red ball and one black ball is transferred from bag A to bag B.

E₃ = Two black balls are transferred from bag A to bag B.

A = Ball drawn from bag B is red.

So,

P(E₁) = $\frac{{^3}{}{C}_2}{{^8}{}{C}_2}$= 3/28

P(E₂) = $\frac{{^3}{}{C}_1 \times {^5}{}{C}_1}{^{8}{}{C}_2}$= 15/28

P(E₃) = $\frac{^{5}{}{C}_2}{^{8}{}{C}_2}$= 10/28

Also,

P(A/E₁) = 6/10

P(A/E₂) = 5/10

P(A/E₃) = 4/10

P(E₁/A) is the required probability, that two red balls were transferred from A to B given that the ball drawn from bag B is red  

So, by using Bayes’ theorem, the required probability is 

= $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)+P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{3}{28} \times \frac{6}{10}}{\frac{3}{28} \times \frac{6}{10} + \frac{15}{28} \times \frac{5}{10} + \frac{10}{28} \times \frac{4}{10}}$

= $\frac{18}{18 + 75 + 40}$

= 18/133

问题 32. 设 d ₁ 、 d ₂ 、 d ₃为三种互斥疾病。令 S 为这些疾病的可观察症状的集合。一位医生从 5000 名患者的随机样本中获得以下信息：1800 名患有疾病 d ₁ ，2100 名患有疾病 d ₂ ，其他人患有疾病 d ₃ 。 1500 名患有疾病 d ₁的患者、1200 名患有疾病 d ₂的患者和 900 名患有疾病 d ₃的患者出现症状。患者最有可能患有哪种疾病？

解决方案：

Let us assume that the events are

A = the patient shows symptoms S

E₁ = has disease d₁

E₂ = has disease​ d₂

E₃ = has disease​ d₃

So, 

P(E₁) = 1800/5000

P(E₂) = 2100/5000

P(E₃) = 1100/5000

Now,

P(A/E₁) =1500/1800

P(A/E₂) = 1200/2100

P(A/E₃) = 900/1100

By using Bayes’ theorem, the required probabilities are

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{1800}{5000} \times \frac{1500}{1800}}{\frac{1800}{5000} \times \frac{1500}{1800} + \frac{2100}{5000} \times \frac{1200}{2100} + \frac{1100}{5000} \times \frac{900}{1100}}$

= $\frac{15}{15 + 12 + 9}$

= 15/36

= 5/12

P(E₂/A) = $\frac{P\left( E_2 \right)P\left( A/ E_2 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{2100}{5000} \times \frac{1200}{2100}}{\frac{1800}{5000} \times \frac{1500}{1800} + \frac{2100}{5000} \times \frac{1200}{2100} + \frac{1100}{5000} \times \frac{900}{1100}}$

= $\frac{12}{15 + 12 + 9}$

= 12/36

= 1/3

P(E₃/A) = $\frac{P\left( E_3 \right)P\left( A/ E_3 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right) + P\left( E_3 \right)P\left( A/ E_3 \right)}$

= $\frac{\frac{1100}{5000} \times \frac{900}{1100}}{\frac{1800}{5000} \times \frac{1500}{1800} + \frac{2100}{5000} \times \frac{1200}{2100} + \frac{1100}{5000} \times \frac{900}{1100}}$

= $\frac{9}{15 + 12 + 9}$

= 9/36

= 1/4

As P(E₁/A ) is maximum, so it is most likely that the person have d₁ disease.

问题 33. 检测特定疾病的测试并非万无一失。该测试将在 90% 的时间内正确检测到疾病，但在 1% 的时间内会错误地检测到疾病。对于估计有 0.2% 患有这种疾病的大量人群，随机选择一个人进行测试，并告知他患有这种疾病。该人实际患有该疾病的可能性有多大？

解决方案：

Let us assume that the events are

A = the person suffers from the disease

E₁ = the test detects the disease correctly 

E₂ = the test does not detect the disease correctly

So, 

P(E₁) = 90/100

P(E₂) = 1/100

Now,

P(A/E₁) = 2/1000

P(A/E₂) = 998/1000

By using Bayes’ theorem, the required probability is

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{90}{100} \times \frac{2}{1000}}{\frac{90}{100} \times \frac{2}{1000} + \frac{1}{100} \times \frac{998}{1000}}$

= $\frac{180}{180 + 998}$

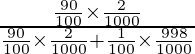
= 180/1178

= 90/589

问题 34. 设 d ₁ 、 d ₂ 、 d ₃ 、 d ₄为三种互斥疾病。令 S 为这些疾病的可观察症状的集合。医生从 5000 名患者的随机样本中获得以下信息：1800 人患有疾病 d ₁ ，2100 人患有疾病 d ₂ ，其他人患有疾病 d ₃ 。 1500 名患有疾病 d ₁的患者、1200 名患有疾病 d ₂的患者和 900 名患有疾病 d ₃的患者出现症状。患者最有可能患有哪种疾病？

解决方案：

Let us assume that the events are

E₁ = The patient had disease d₁

E₂ = The patient had disease d₂

E₃ = The patient had disease d₃

S = The patient showed the symptom

Also, E₁, E₂, and E₃ are mutually exclusive and exhaustive events.

So, 

P(E₁) = 1800/1500 = 18/50

P(E₂) = 2100/5000 = 21/50

P(E₃) = 1100/5000 = 11/50

Now,  

P(S/E₁) = The probability that the patient had disease d₁ and showed symptoms S = 1500/5000 = 15/50

P(S/E₂) = The probability that the patient had disease d₂ and showed symptoms S = 1200/5000 = 12/50

P(S/E₃) = The probability that the patient had disease d₃ and showed symptoms S = 900/5000 = 9/50

By using Bayes’ theorem,

P(E₁/S) is the probability that patient had disease d₁ such that symptoms of d₁ appears

= $\frac{P\left( E_1 \right)P\left( \frac{S}{E_1} \right)}{P\left( E_1 \right)P\left( \frac{S}{E_1} \right) + P\left( E_2 \right)P\left( \frac{S}{E_2} \right) + P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}$

= $\frac{\frac{18}{50} \times \frac{15}{50}}{\frac{18}{50} \times \frac{15}{50} + \frac{21}{50} \times \frac{12}{50} + \frac{11}{50} \times \frac{9}{50}}$

= 270/621

P(E₂/S) is the probability that patient had disease d₂ such that symptom of d₂ appears

= $\frac{P\left( E_2 \right)P\left( \frac{S}{E_2} \right)}{P\left( E_1 \right)P\left( \frac{S}{E_1} \right) + P\left( E_2 \right)P\left( \frac{S}{E_2} \right) + P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}$

= $\frac{\frac{21}{50} \times \frac{12}{50}}{\frac{18}{50} \times \frac{15}{50} + \frac{21}{50} \times \frac{12}{50} + \frac{11}{50} \times \frac{9}{50}}$

= 252/621

P(E₃/S) is the probability that patient had disease d₃ such that symptom of d₃ appears

= $\frac{P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}{P\left( E_1 \right)P\left( \frac{S}{E_1} \right) + P\left( E_2 \right)P\left( \frac{S}{E_2} \right) + P\left( E_3 \right)P\left( \frac{S}{E_3} \right)}$

= $\frac{\frac{11}{50} \times \frac{9}{50}}{\frac{18}{50} \times \frac{15}{50} + \frac{21}{50} \times \frac{12}{50} + \frac{11}{50} \times \frac{9}{50}}$

= 99/621

Hence, P(E₁/A) is the maximum, then the patient is most likely to have the disease d₁.

问题 35. 众所周知，A 在 5 次中说真话 3 次。他扔了一个骰子并报告说它是一个。找出它实际上是一的概率。

解决方案：

Let us assume that the events are

A = the man reports the appearance of 1 on throwing a die

E₁ = 1 occurs 

E₂ = 1 does not occur

So, 

P(E₁) = 1/6

P(E₂) = 5/6

Now,

P(A/E₁) = 3/5

P(A/E₂) = 2/5

By using Bayes’ theorem, the required probability is

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{1}{6} \times \frac{3}{5}}{\frac{1}{6} \times \frac{3}{5} + \frac{5}{6} \times \frac{2}{5}}$

= $\frac{3}{3 + 10}$

= 3/13

问题 36. A 说真话 10 次中有 8 次。掷骰子。他报告说它是 5。它实际上是 5 的概率是多少？

解决方案：

Let us assume that A be the event that man reports that 5 occurs and E the event that 5 actually turns up.

So, 

P(E) = 1/6

$P(\overline{E})$ = 1 – 1/6 = 5/6

Also,  

P(A/E)  = Probability that man reports that 5 occurs given that 5 actually turns up 

= Probability of man speaking the truth 

= 8/10

= 4/5

$P\left(A/\overline{E}\right)$= Probability that man reports that 5 occurs given that 5 does not turns up 

= Probability of man not speaking the truth 

=  1 – 4/5

= 1/5

Therefore, the required probability = P(E/A)

= $\frac{P\left( E \right)P\left( \frac{A}{E} \right)}{P\left( E \right)P\left( \frac{A}{E} \right) + P\left(\overline{ (E) } \right)P\left( \frac{A}{\overline{(E)}} \right)}$

= $\frac{\frac{1}{6} \times \frac{4}{5}}{\frac{1}{6} \times \frac{4}{5} + \frac{5}{6} \times \frac{1}{5}}$

= 4/9

问题 37。在回答多项选择测试的问题时，学生要么知道答案，要么猜测。假设 3/4 是他知道答案的概率，而 1/4 是他猜测的概率。假设一个学生猜对答案的概率为 1/4。如果学生回答正确，他知道答案的概率是多少？

解决方案：

Let us assume that the events are

A = the answer is correct

E₁ = the student knows the answer

E₂ = the student guesses the answer

So, 

P(E₁) = 3/4

P(E₂) = 1/4

Now, 

P(A/E₁) = 1

P(A/E₂) = 1/4

By using Bayes’ theorem, the required probability is

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{\frac{3}{4} \times 1}{\frac{3}{4} \times 1 + \frac{1}{4} \times \frac{1}{4}}$

= 3/3 + 1/4

= 12/13

问题 38. 实验室验血在检测某种疾病时的有效率为 99%。但是，该测试也会对 0.5% 的健康人测试产生假阳性结果（即，如果测试一个健康人，那么测试将暗示他患有该疾病的概率为 0.005）。如果 0.1% 的人口实际上患有这种疾病，那么如果一个人的检测结果是阳性的，那么他患有这种疾病的概率是多少？

解决方案：

Let us assume that E₁ and E₂ be the events that a person has a disease and a person has no disease.

Also, E₁ and E₂ are complimentary to each other.

So, P(E₁) + P(E₂) = 1

P(E₁) = 0.001

=>  P (E₂) = 1 − P (E₁) = 1 − 0.001 = 0.999

Let us assume that A be the event that the blood test result is positive.

Now,

P(A/E₁) = 99% = 0.99

P(A/E₂) = 0.5 % = 0.005

By using Bayes’ theorem, the required probability is

P(E₁/A) = $\frac{P\left( E_1 \right)P\left( A/ E_1 \right)}{P\left( E_1 \right)P\left( A/ E_1 \right) + P\left( E_2 \right)P\left( A/ E_2 \right)}$

= $\frac{0 . 001 \times 0 . 99}{0 . 001 \times 0 . 99 + 0 . 999 \times 0 . 005}$

= 990/5985

= 22/133

问题 39. 一个 60 名学生的班级有三类学生：

A：非常勤奋； B：有规律但不那么勤奋； C：粗心不规则 10名学生在A类，30名在B类，其余在C类。发现A类学生在期末考试中无法获得好成绩的概率为0.002， B 类是 0.02，C 类的概率是 0.20。随机抽取的一名学生被发现在考试中未能取得好成绩。求这个学生属于 C 类的概率。

解决方案：

Let us assume that the events are

E = the student could not get good marks in the examination.

A = student is very hardworking

B = student is regular but not so hardworking

C = student is careless and irregular

Here, we have

P(A) = 10/60

P(B) =  30/60

P(C) = 20/60

Also,

P(E/A)  = Probability that category A student could not get good marks in the examination = 0.002  

P(E/B) = Probability that a category B student could not get good marks in the examination = 0.02

P(E/C)  = Probability that a category C student could not get good marks in the examination = 0.2

So, P(C/E) is the required probability 

= $\frac{P\left( C \right)P\left( \frac{E}{C} \right)}{P\left( A \right)P\left( \frac{E}{A} \right) + P\left( B \right)P\left( \frac{E}{B} \right) + P\left( C \right)P\left( \frac{E}{C} \right)}$

= $\frac{\frac{20}{60} \times 0 . 2}{\frac{10}{60} \times 0 . 002 + \frac{30}{60} \times 0 . 02 + \frac{20}{60} \times 0 . 2}$

= 4/4.62

= 400/462

= 200/231