问题35.在图中,AB和CD是彼此垂直的圆的两个直径,OD是较小圆的直径。如果OA = 7厘米,请找到阴影区域的面积。
解决方案:
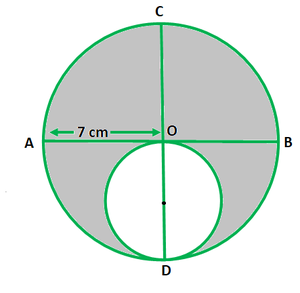
Given that,
Radius of larger circle(OA) = 7 cm
Diameter of smaller circle(OD) = 7 cm
So, the radius of smaller circle = 7/2 cm
Now we find the area of the shaded region = Area of large circle – Area of small circle
= π(7)2 – π(7/2)2
= π × 49 – π × (49/4)
= 22/7[49 – 49/4]
= 115.5cm2
Hence, the area of the shaded region 115.5 cm2
问题36.在图中,PSR,RTQ和PAQ是三个直径分别为10 cm,3 cm和7 cm的半圆形。找到阴影区域的周长。
解决方案:
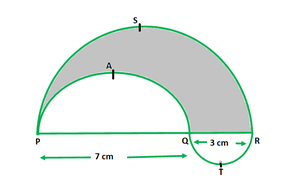
Given that,
Diameter of semicircle PSR = 10 cm
So, radius of semicircle PSR, (r1) = 10/2 = 5 cm
Diameter of semicircle RTQ = 3 cm
So, radius of semicircle RTQ, (r2) = 3 cm = 3/2 cm
Diameter of semicircle PAQ = 7 cm
So, radius of semicircle PAQ, (r3) = 7/2 cm
Now we find the perimeter of the shaded region = Length of the arc PAQ +
Length of the arc PSR +
Length of the arc RTQ
= πr1 + πr2 + πr3
= π(r1 + r2 + r3)
= π(5 + 3/2 + 7/2)
= π{(10 + 3 + 7)/2}
= π × 20/2
= 10 π
= 10 × 22/7
= 10 × 3.14
= 31.4 cm
Hence, the perimeter of the shaded region is 31.4 cm
问题37.在图中,两个圆心分别为A和B的圆在C点相互接触。如果AC = 8 cm,AB = 3 cm,则找到阴影区域。
解决方案:
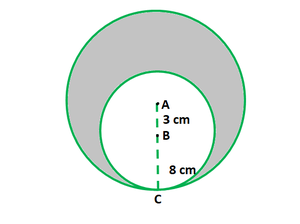
Given that,
AC = 8 cm & AB = 3 cm
Here, AC is the radius of the bigger circle and BC is the radius of inner circle.
BC = AC – AB
BC = 8 – 3
BC = 5 cm
Now we find the area of shaded region = Area of bigger circle – Area of inner circle
= πR2 – πr2
= π(R2 – r2)
= 22/7 (82 – 5)
= 22/7 (64 – 25)
= 22/7 × 39
= (22 × 39)/7
= 858/7
= 122.57 cm2
Hence, the area of shaded region is 122.57 cm2
问题38.在图中,ABCD是面2a的正方形。找出两者之间的比例
(i)周长
(ii)正方形的外接圆和外接圆的面积。
解决方案:
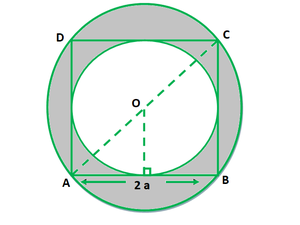
Given that,
Side of a square ABCD = 2a
So, the diameter of incircle = side of a square = 2a
Radius of a incircle(r) = Diameter of incircle/2
r = 2a/2
r = a
Also, the diameter of circumcircle = diagonal of a square = √2 side
So, the radius of circumcircle(R) = √2 side/2
R = (√2 × 2a) /2
R = √2a
R = √2a
(i) Ratio of circumferences of inner circle (C1) and circumcircle (C2)
C1 : C2 = 2πr : 2πR
C1 / C2 = 2πr / 2πR
C1 / C2 = r / R
C1 / C2 = a/√2a
C1 / C2 = 1/√2
C1 : C2 = 1 : √2
(ii) Ratio of Areas of inner circle (A1) and circumcircle (A2) :
A1 : A2 = πr2 : πR2
A1 / A2 = πr2 / πR2
A1 / A2 = r2 /R2
A1 / A2 = a2/(√2a)2
A1 / A2 = a2/2a2
A1 / A2 = 1/2
A1 : A2 = 1 : 2
Hence, the ratio of circumferences of inner circle (A1) and circumcircle (A2) is 1 : √2
and Ratio of Areas of inner circle (A1) and circumcircle (A2) is 1 : 2
问题39.在图中,显示了三个半圆A,B和C,每个直径为3 cm,另一个半圆E的圆D为直径4.5 cm。计算 :
(i)阴影区域的面积
(ii)将阴影区域的油漆成本以每平方厘米25帕斯卡的比率计至最接近的卢比
解决方案:

Given that,
Three semicircles, A, B and C having diameter 3 cm each, and
another semicircle E having a circle D with diameter 4.5 cm.
(i) Now area of shaded region = Area of the semicircle with diameter 9 cm –
Area of two semicircles with radius 3 cm –
Area of the circle with centre D +
Area of semicircle with radius 3 cm
= 1/2 π(9/2)2 – 2 × 1/2 π(3/2)2 – π(4.5/2)2 + 1/2 π(3/2)2
= 1/2 π(4.5)2 – π(1.5)2 – π(2.25)2 + 1/2 π(1.5)2
= 1/2 π(4.5)2 – π(1.5)2 + 1/2 π(1.5)2 – π(2.25)2
= 1/2 π(4.5)2 – 1/2 π(1.5)2 – π(2.25)2
= 1/2π(4.52 – 1.52) – π 2.252
= 1/2 π (20.25 – 2.25) – π × 5.0625
= 1/2 π(18) – π × 5.0625
= 9π – π 5.0625
= π(9 – 5.0625)
= π × 3.9375
= 22/7 × 3.9375
= 0.5625 × 22
= 12.375 cm2
(ii) Cost of painting 1 cm² Shaded Region = 25 p
Cost of painting 13.275 cm² Shaded Region = 25 p × 13.275
= 309.375 paise
= ₹ 309.375 /100
= ₹ 3 (nearest rupee)
Cost of painting the Shaded Region = ₹ 3.
Hence, the area of the shaded region is12.375 cm2 and the cost of painting the Shaded Region is ₹ 3.
问题40.在图中,ABC是一个直角三角形,∠B= 90°,AB = 28 cm,BC = 21 cm。以AC为直径绘制一个半圆,以BC为半径绘制一个四分之一圆。找到正确的阴影区域的面积小数点后两位。
解决方案:
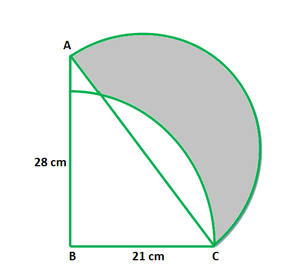
Given that,
ABC is a right-angled triangle, ∠B = 90°, AB = 28 cm and BC = 21 cm.
AC as diameter a semicircle is drawn and with BC as radius a quarter circle is drawn
So, the area of triangle = 1/2 x 21 x 28 = 294 cm2
Now in ΔABC,
By using Pythagoras Theorem
AC2 = 282 + 212
AC = √1225
AC = 35
So, the radius of semi-circle = 35/2 = 17.5
Now, the area of semi-circle
= 1/2 x 3.14 x (17.5)2 = 480.8 cm2
Area of quarter circle = 1/4 x 3.14 x 212 = 346.2 cm2
Now we find the area of the shaded region = Area of Semi-circle + Area of triangle ABC –
Area of quarter circle
= 294 + 480.8 – 346.2 = 428.75cm2
Hence, the area of shaded region is 428.75cm2
问题41.在图中,O是圆弧的中心,而AOB是直线。找到正确的阴影区域的周长和面积,精确到小数点后一位。 (取π= 3.142)
解决方案:

Given that,
∆ACB is a right-angled triangle, in which AC = 12 cm, BC = 16 cm, ∠C = 90°
Now In ∆ACB,
By using Pythagoras theorem, we get
AB2 = AC2 + BC2
AB2 = 122 + 162
AB2 = 144 + 256
AB2 = 400
AB = √400
AB = 20 cm
So, the diameter of a semicircle = 20 cm
So, the radius of semicircle, r = 10 cm
Now we find the perimeter of a Shaded region = circumference of semicircle + AC + AB
= πr + 12 + 16
= 3.142 × 10 + 28
= 31.42 + 28
= 59.42 cm
Now we find the area of the shaded region = Area of a semicircle – Area of a right angle triangle
= 1/2 πr2 – 1/2 × base × height
= 1/2 × 3.142 × 102 – 1/2 × AC × BC
= 1/2 × 3.142 × 100 – 1/2 × 12 × 16
= 3.142 × 50 – 6 × 16
= 157.1 – 96
= 61.1 cm2
Hence, the required Perimeter of a Shaded region is 59.4 cm and area of the shaded region is 61.1 cm2.
问题42.在图中,阴影区域的边界由四个半圆弧组成,最小的两个圆弧相等。如果最大直径为14厘米,最小直径为3.5厘米,请找到
(i)边界的长度,
(ii)阴影区域的面积。
解决方案:

Given that,
The shaded region consists of four semi-circular arcs,
the smallest two being equal.
If the diameter of the largest is 14 cm and of the smallest is 3.5 cm.
(i) Length of the boundary = (boundary of bigger semicircle +
boundary of smaller semicircle +
2 × boundary of smallest semicircle)
= π(14/2) + π(7/2) + 2× π(3.5/2)
= 7π + 3.5π + 3.5π
= 7π + 7π
= 14π
= 14 × 22/7
= 2 × 22
= 44 cm
Hence, the length of the boundary = 44 cm
(ii) Now we find the area of the shaded region = Area of semicircle with AB as diameter –
Area of the semicircle with radius AE –
Area of the semicircle with radius BC +
Area of semicircle with diameter 7 cm
= 1/2 × π(14/2)2 – 1/2 × π(3.5/2)2 – 1/2 × π(3.5/2)2 + 1/2 × π(7/2)2
= 1/2π [72 – 1.752 – 1.752 + 3.52]
= 1/2 π[49 – 3.0625 – 3.0625 + 12.25]
= 1/2 π[49 – 6.125 + 12.25]
= 1/2 π [42.875 + 12.25]
= 1/2 π [55.125]
= 1/2 × 22/7 × 55.125
= 11 × 7.875
= 86.625 cm2
Hence, the required area of the shaded region is 86.625 cm2
问题43.在图中,AB = 36厘米,M是AB的中点。在AB,AM和MB上绘制半圆作为直径。中心为C的圆触及所有三个圆。找到阴影区域的面积。
解决方案:
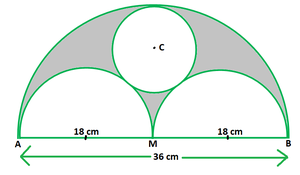
Given that,
AB = 36 cm
AM = BM = 1/2 × AB = 1/2 × 36 = 18 cm [M is mid-point of AB]
AM = BM = 18 cm
AP = PM = MQ = QB = 9 cm
Let us considered the radius of circle with centre C be ‘r’ i.e CR = r
Join P to C and M to C, MC ⊥ AB
MR = AM = 18 cm
CM = MR – CR
CM = (18 – r )………(1)
PC = PE + CE
PC = (9 + r)…….(2)
Now In ∆ PCM,
By using Pythagoras theorem, we get
PC2 = PM2 + MC2
(9 + r)2 = 92 + (18 – r)2
81 + r2 + 18r = 81 + 324 + r2 – 36r [From eq (1) and (2)]
54r = 324
r = 324/54
r = 6
Radius of circle with C as a centre = 6 cm
Now we find the area of shaded region = Area of semicircle with diameter AB –
Area to semicircles with diameter AM and MB –
Area of circle with C as a centre
= 1/2 π(36/2)2 – 2 × 1/2 π(18/2)2 – π(6)2
= 1/2 π(18)2 – π(9)2 – π(6)2
= 1/2 π × 324 – 81π – 36π
= 162π – 81π – 36π
= 162π – 117π
= 45π cm2
Hence, the area of required shaded region is 45π cm2.
问题44.在图中,ABC是一个直角三角形,其中∠A= 90°,AB = 21 cm,AC = 28 cm。半圆在AB,BC和AC上以直径表示。找到阴影区域的面积。
解决方案:
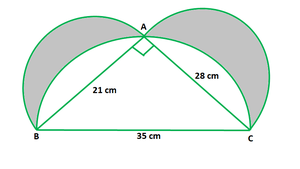
Given that,
ABC is a right-angled triangle in which ∠A = 90°, AB = 21 cm and AC = 28 cm.
To find: the area of the shaded region.
Now In right ΔABC,
By using Pythagoras theorem, we get
BC2 = AB2 + AC2
BC2 = 212 + 282
BC2 = 1225
BC = √1225
BC = 35 cm
Diameter BC = 35 cm
Now we find the area of shaded region, A = Area of semicircle with AC as a diameter +
Area of right angle ∆ ABC +
Area of semicircle with AB as a diameter –
Area of semicircle with BC as diameter
= 1/2 π(21/2)2 + 1/2 π(28/2)2 + 1/2 × 21 × 28 – 1/2 π(35/2)2
= 1/2 π(21/2)2 + 1/2 π(28/2)2 – 1/2 π(35/2)² + 1/2 × 21 × 28
= 1/2 π [10.52 + 142 – 17.52] + 14 × 21
= 1/2 π [110.25 + 196 – 306.25] × 294
= 1/2 π [306.25 – 306.25] + 294
= 1/2 π × 0 + 294
= 0 + 294
= 294 cm2
Hence, the area of required shaded region is 294 cm2
问题45.在图中,显示了铁路隧道的横截面。圆形部分的半径OA为2 m。如果∠AOB= 90°,则计算:
(i)隧道的高度
(ii)横截面的周长
(iii)横截面积。
解决方案:

Given that,
The radius OA of the circular part = 2 m
∠AOB = 90°
Let OM ⊥ AB.
(i) Now In ∆OAB,
By using Pythagoras Theorem, we get
AB2 = OA2 + OB2
AB2 = 22 + 22
AB2 = 8
AB = √8
AB = √4×2
AB = 2√2 cm
Here, D b e the mid point so, AD = BD = √2
So, OD2 = OA2 – AD2
= 22 – (√22)
= √2
Let the height of the tunnel to be h.
So,
The area of ∆ OAB = 1/2 × Base × height
= 1/2 × OA × OB
1/2 × 2 × 2
= 2
(i) Height of the tunnel (h) = OC + OD
h = √2 + 2
h = (2 + √2)m
(ii) Central angle of major arc, θ = 360° – 90° = 270°
Perimeter of cross-section,
= length of the major Arc AB + AB
= θ/360° × 2πr + 2√2
= 270°/360° × 2π × 2 + 2√2
= 3/4 × 4π + 2√2
= (3π + 2√2) m
(iii) Area of cross-section, A = θ/360° × Area of circle + area of ∆AOB
= θ/360° × πr2 + 1/2 × base × height
= 270°/360° × π× 22 + 1/2 × 2 × 2
= 3/4 × π × 4 + 2
= (3π + 2)m
Hence, the height of the tunnel is (2 + √2)m,
Perimeter of cross-section is (3π + 2√2) m and
Area of cross section is (3π + 2)m.
问题46.在图中显示了一个风筝,其中BCD是半径为42 cm的圆的象限形状。 ABCD是一个正方形,ΔCEF是一个等腰直角三角形,其相等的边长为6 cm。找到阴影区域的面积。
解决方案:
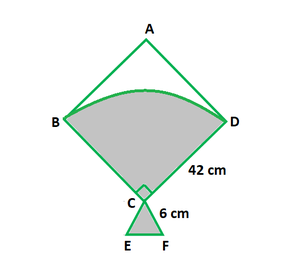
Given :
Radius of a quadrant of a circle, r = 42 cm.
Equal sides of an isosceles right-angled ∆ = 6 cm
To find: the area of the shaded region.
Now we find the area of shaded region(A) = Area of quadrant + Area of isosceles ∆
A = 1/4 πr2 + 1/2 × base × height
A = 1/4 × 22/7 × 422 + 1/2 × 6 × 6
A = 1/2 × 11 × 6 × 42 + 18
A = 11 × 3 × 42 + 18
A = 33 × 42 + 18
A = 1386 + 18
A = 1404 cm2
Hence, the area of shaded region is 1404 cm2
问题47.在图中,ABCD是面积为24.5 cm2的梯形。在其中,AD || BC,∠DAB= 90°,AD = 10 cm,BC = 4 cm。如果ABE是圆的象限,请找到阴影区域的面积。 (取π=(22/7)。
解决方案:

Given,
Area of trapezium ABCD, A = 24.5 cm2
AD || BC, ∠DAB = 90°, AD = 10 cm, BC = 4 cm and ABE is quadrant of a circle.
Now in trapezium ABCD,
Area of the trapezium, A = 1/2 (sum of parallel sides) × perpendicular distance between the parallel sides(h)
A = 1/2 (AD + BC) × AB
24.5 = 1/2 (10 + 4) × AB
24.5 × 2 = 14 AB
AB = 49/14
AB = 7/2
AB = 3.5 cm
So, the radius of the quadrant of the circle, r = AB = 3.5 cm
Area of the quadrant of the circle = 1/4 ×πr2
= (1/4) (22/7 x 3.5 x 3.5)
= 9.625 cm2
Now we find the area of the shaded region = Area of the trapezium – Area of the quadrant of the circle
= 24.5 – 9.625
= 14.875 cm2
Hence, the area of the shaded region is 14.875 cm2
问题48.在图中,ABCD是带有AB ||的梯形。 DC,AB = 18厘米,DC = 32厘米,AB和DC之间的距离为14厘米。已绘制出半径为7厘米,中心为A,B,C和D的圆。然后,找到图形阴影区域的区域。 (使用π= 22/7)。
解决方案:

Given,
AB = 18 cm, DC = 32 cm,
Distance between AB and DC(h)= 14 cm and radius of each circle(r) = 7cm
Since, AB ||DC
So, ∠A + ∠D = 180° & ∠B + ∠C = 180°
Area of sector = (θ /360) × πr2
Area of sector with ∠A and ∠D = (180 /360) × 22/7 × 72
= 1/2 × 22 × 7 = 11 × 7 = 77 cm2
Similarly, Area of sector with ∠B & ∠C = (180 /360) × 22/7 × 72
= 1/2 × 22 × 7 = 11 × 7 = 77 cm2
Now in trapezium ABCD,
Area of trapezium = 1/2 (sum of parallel sides) × perpendicular distance between Parallel sides(h)
= 1/2 (AB + DC) × (h)
= 1/2(18 + 32) × 14
= 1/2(50)× 14
= 25 × 14 = 350 cm2
Now we find the area of shaded region = Area of trapezium –
(Area of sector with ∠B and ∠C +
Area of sector with ∠A and ∠D )
= 350 -(77+77) = 350 – 154 = 196 cm2
Hence, the Area of shaded region is 196 cm2
问题49.从梯形ABCD形状的薄金属片中,其中AB ||。 CD和∠BCD= 90°,去掉了四分之一圈的BEFC(见图)。给定AB = BC = 3.5厘米,DE = 2厘米,请计算剩余的金属板面积。
解决方案:
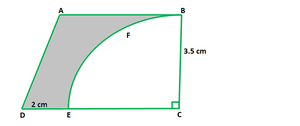
Given,
In trapezium ABCD
AB || CD and ∠BCD = 90°
AB = BC =3.5 cm & DE = 2 cm
CE = CB = 3.5 cm [CE and BC are the radii of quarter circle BFEC]
So, DC = DE + EC
DC = 2 cm + 3.5 cm
DC = 5.5 cm
Area of remaining piece of the metal sheet (A) = Area of trapezium ABCD – Area of quarter circle BFEC
A = 1/2(AB + DC) × BC – 1/4 x π x (BC)2
A = 1/2 (3.5 + 5.5) × 3.5 – 1/4 x π(3.5)2
A = 1/2 × 9 × 3.5 – 1/4 x π(3.5)2
A = 4.5 × 3.5 – 22/7 × 3.5 × 3.5/4
A = 15.75 – 11 × 3.5/4
A = 15.75 – 9.625
A = 6.125 cm2
Hence, the area of remaining piece of the metal sheet (Shaded region) is 6.125 cm2
问题50.在图中,ABC是边长为8厘米的等边三角形。 A,B和C是半径为4 cm的圆弧的中心。找到阴影区域的面积,正确的小数点后两位。 (取π= 3.142和√3= 1.732)。
解决方案:
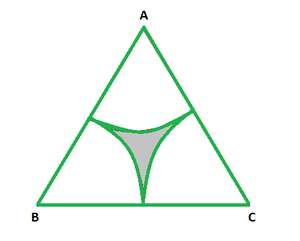
In Equilateral triangle all the angles are each 60°.
The corners form sectors of a circle.
When we join the sectors we form a major sector with the middle angle as (60 × 3) = 180°
Area of the shaded region = Area of the triangle – area of the sector.
Area of the triangle = 1/2 × base × height
As we know that,
Base = 8/2 = 4 cm
Hypotenuse = 8 cm
Height = √82 – 42
= √48
= 4√3
= 4 × 1.732
= 6.928 cm
Also, area of the triangle = 1/2 × 6.928 × 8 = 27.712 cm2
Now area of the Sector,
Radius of the sector = 8/2 = 4 cm
= 180/360 × 3.142 × 42 = 25.136 cm2
Now we find the area of the shaded region = 27.712 – 25.136 = 2.576 cm2
Hence, the area of the shaded region is 2.576 cm2
问题51.三角形场的边为15 m,16 m和17 m。在田地的三个角落,一头牛,水牛和一匹马分别用长7 m的绳子捆在一起,在田里放牧。找到无法被三只动物放牧的领域。
解决方案:
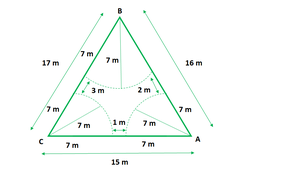
Let ABC be the triangular field with sides AC = 15 m, AB = 16 m and BC = 17 m
And,
Let the place where the buffalo, the horse and the cow are tied,
are three sectors i.e. sector BFG, sector CHI and sector ADE
Area of triangular field = √s(s – a)(s – b)(s – c) [by using Heron’s formula]
s = (a + b + c)/2
s = (15 + 16 + 17)/2
s = 48/2
s = 24 m
=√24(24 – 15)(24 – 16)(24 – 17)
=√24 x 9 x 8 x 7
=√12096
=109.98 m2
Area of triangular field = 109.98 m2
Area of the grazed part = Area of the sector ADE + Area of sector BFG + Area of sector CHI
= π x 72 x ∠A/360 + π x 72 x ∠B/360 + π x 72 x ∠C/360
= π x 72(∠ A + ∠ B + ∠ C)/360
= 22/7 x (7)2 x 180/360
= 154/2
= 77 m2
So, the area of the field which cannot be grazed by these animals
= 109.98 m2 – 77 m2
= 32.98 m2
Hence, the area of the field which cannot be grazed by these animals is 32.98 m2
问题52.在给定的图中,正方形的边长为28厘米,每个圆的半径为正方形的边长的一半,其中O和O’为圆心。找到阴影区域的面积。
解决方案:
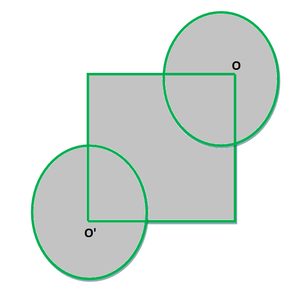
Given that,
Side of square = 28 cm
Radius of each circle is half of the length of the side of the square
So, radius of each circle = 28/2 cm =14 cm
As we know that
Area of Square = (Side)2
Area of Circle = πr2
Now we find the area of Shaded region = Area of Square +3/4 (Area of Circle) + 3/4(Area of Circle)
= (28)2 + 3/2 x 22/7 × 14 × 14
= 784 cm2 + 924 cm2
= 1708 cm2
Hence, the area of shaded region is 1708 cm2
问题53:在医院中,用过的水被收集在直径为2 m,高度为5 m的圆柱形水箱中。回收后,这些水用于将公园灌溉到医院,该医院的长度为25 m,宽度为20 m。如果水箱已完全注满,那么用于灌溉公园的静水高度将是多少?
解决方案:
Given that
Diameter of cylinder (d) = 2 m
Radius of cylinder (r) = 1 m
Height of cylinder (H) = 5 m
Now we know that volume of cylindrical tank is,
V = πr2H = π × (1)2 × 5 = 5π m
Length of the park (l) = 25 m
Breadth of park (b) = 20 m
Let us considered the height of standing water in the park = h
Volume of water in the park = l x b x h = 25 × 20 × h
Now for irrigation in the park water is used from the tank. So,
Volume of cylindrical tank = Volume of water in the park
⇒ 5π = 25 × 20 × h
⇒ 5π/25 × 20 = h
⇒ h = π/100 m
⇒ h = 0.0314 m
Hence, the height of standing water used for irrigating the park is 0.0314 m