第 12 类 RD Sharma 解决方案 – 第 15 章均值定理 – 练习 15.2

问题 1 (i)。在指定的间隔上验证以下函数的拉格朗日平均值定理。在每种情况下，在 [2, 3] 上的拉格朗日均值定理 f(x) = x ² – 1 中找到指定区间中的点 'c'

解决方案：

Given that 

f(x) = x² – 1

Since the given f(x) = x² – 1 is a polynomial function. 

So, the given f(x) is continuous on [2, 3] and differentiable in (2, 3)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (2, 3) such that, 

$f'(c)=\frac{f(3)-f(2)}{3-2}\\ 2c=\frac{((3)^2-1)((2)^2-1)}{1}$

2c = (8 – 3)

c = 5/2 ∈ (2, 3)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (ii)。验证拉格朗日的平均值定理在指定的时间间隔以下。在每种情况下，在 [0, 1] 上的拉格朗日平均值定理 f(x) = x ³ – 2x ² – x + 3 中找到指定区间中的点“c”。

解决方案：

Given that 

f(x) = x³ – 2x² – x + 3

Since the given f(x) = x³ – 2x² – x + 3 is a polynomial function. 

So, the given f(x) is continuous on [0, 1] and differentiable in (0, 1)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, 1) such that, 

$f'(c)=\frac{f(1)-f(0)}{1-0}\\ 3c^2-4c-1=\frac{[(1)^2-2(1)^2-(1)+3]-3}{1}$

3c² – 4ac – 1 = 1 – 3

3c² – 4c + 1 = 0

3c² – 3c – c + 1 = 0

3c(c – 1) – 1(c – 1) = 0

(3c – 1)(c – 1) = 0

c = 1/3 ∈ (0, 1)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (iii)。在指定的间隔上验证以下函数的拉格朗日平均值定理。在每种情况下，在 [1, 2] 上的拉格朗日均值定理 f(x) = x(x – 1) 中找到指定区间中的点“c”。

解决方案：

Given that 

f(x) = x(x – 1) ⇒ x² – x

Since the given f(x) = x² – x is a polynomial function. 

So, the given f(x) is continuous on [1, 2] and differentiable in (1, 2)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 2) such that, 

$f'(c)=\frac{f(2)=f(1)}{2-1}\\ 2c-1=\frac{(4-2)-(1-1)}{1}\\ 2c-1=\frac{2-0}{1}$ 

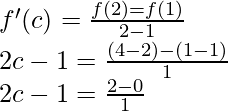
2c = 3

c = 3/2 ∈ (1, 2)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (iv)。验证指示区间上以下函数的拉格朗日均值定理。在每种情况下，在 [-1, 2] 上的拉格朗日平均值定理 f(x) = x ² – 3x + 2 中找到指定区间中的点“c”。

解决方案：

Given that 

f(x) = x² – 3x + 2 

Since the given f(x) = x² – 3x + 2 is a polynomial function. 

So, the given f(x) is continuous on [-1, 2] and differentiable in (-1, 2)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (-1, 2) such that, 

$f'(c)=\frac{f(2)-f(-1)}{2+1}\\ 2c-3=\frac{(4-6+2)-(1+3+2)}{3}\\ 2c-3=-\frac{6}{3}$ 

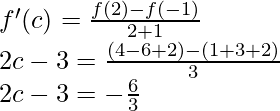
2c – 3 = -2

2c = 1

c = 1/2 ∈ (-1, 2)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (v)。在指定的间隔上验证以下函数的拉格朗日平均值定理。在每种情况下，在 [1, 3] 上的拉格朗日平均值定理 f(x) = 2x ² – 3x + 1 中找到指定区间中的点“c”。

解决方案：

Given that, 

f(x) = 2x² – 3x + 1 

Since the given f(x) = 2x² – 3x + 1 is a polynomial function. 

So, the given f(x) is continuous on [1, 3] and differentiable in (1, 3)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 3) such that, 

$f'(c)=\frac{f(3)-f(1)}{3-1}\\ 4c-3=\frac{(2(3)^2-3(3)+1)-(2-3+1)}{3-1}\\ 4c-3=\frac{10}{2}$

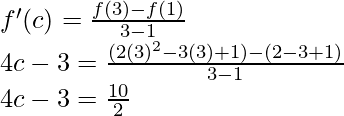
4c – 3 = 5

4c = 5 + 3

4c = 8

c = 2 ∈ (1, 3)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (vi)。在指定的间隔上验证以下函数的拉格朗日平均值定理。在每种情况下，在 [1, 5] 上的拉格朗日平均值定理 f(x) = x ² – 2x + 4 中找到指定区间中的点“c”。

解决方案：

Given that, 

f(x) = x² – 2x + 4 

Since the given f(x) = x² – 2x + 4 is a polynomial function. 

So, the given f(x) is continuous on [1, 5] and differentiable in (1, 5)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 5) such that, 

$f'(c)=\frac{f(5)-f(1)}{5-1}\\ 2c-2=\frac{((5)^2-2(5)+4)-(1-2+4)}{4}\\ 2c-2=\frac{19-3}{4}$

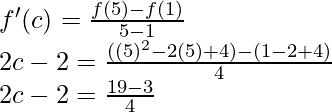
2c – 2 = 16/4

2c – 2 = 4

2c = 6

c = 3 ∈ (1, 5)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (vii)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日平均值定理 f(x) = 2x – x ² on [0, 1] 所示，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = 2x – x²

Since the given f(x) = 2x – x² is a polynomial function. 

So, the given f(x) is continuous on [0, 1] and differentiable in (0, 1)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, 1) such that, 

$f'(c)=\frac{f(1)-f(0)}{1-0}\\ 2-2c=\frac{(2(1)-(1)^2)-(0)}{1}$ 

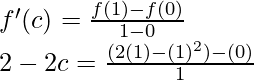
2 – 2c = 1

1 = 2c

c = 1/2 ∈ (0, 1)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (viii)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日平均值定理 f(x) = (x – 1)(x – 2)(x – 3) 在 [0, 4] 上，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = (x – 1)(x – 2)(x – 3)

Since the given f(x) = (x – 1)(x – 2)(x – 3) is a polynomial function. 

So, the given f(x) is continuous on [0, 4] and differentiable in (0, 4)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, 4) such that, 

$f'(c)=\frac{f(4)-f(0)}{4-0}$

(c – 1)(c – 2) + (c – 2)(c – 3) + (c – 1)(c – 3)$=\frac{(3)(2)(1)-(-1)(-2)(-3)}{4-0}$

c² – 3c + 2 + c² + 5c + 6 + c² – 4c + 3 $=\frac{6+6}{4}$

3c² – 12c + 11 = 3

3c² = 12c + 8 = 0

$c=\frac{-(-12)±\sqrt{144-4*3*8}}{6}\\ c=\frac{12±\sqrt{48}}{6}\\ c=2±\frac{2\sqrt{3}}{3}∈(0,4)\\ c=2±\frac{2}{\sqrt{3}}∈(0,4)$

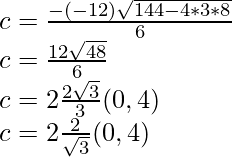
Hence, the Lagrange’s mean value theorem is verified.

问题 1 (ix)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日均值定理 f(x) 所述，在每个指定区间中找到一个点“c” 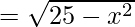$=\sqrt{25-x^2}$在 [-3, 4] 上。

解决方案：

Given that, 

f(x) $=\sqrt{25-x^2}$

The given f(x) is exists, if 

25 – x² ≥ 0

x² ≤ 25

x ≤ ±5

-5 < x < 5

So, f(x) has unique value ∀ x ∈(-5. 5), so the given f(x) is continuous on [-3, 4].

Now, differentiate f(x) = (25 – x²)^1/2 with respect to x, we get

f'(x) = 1/2(25 – x²)^1/2-1d(25 – x²)/dx$=\frac{-2x}{2\sqrt{25-x^2}} =\frac{-x}{\sqrt{25-x^2}}$

So, f'(x) exists∀ x ∈ (-3, 4), hence, f(x) is differential on (-3, 4).

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (-3, 4) such that, 

$f'(c)=\frac{f(4)-f(-3)}{4+3}\\ \frac{-2c}{2\sqrt{25-c^2}}=\frac{\sqrt{9}-\sqrt{16}}{7}\\ -7c=-\sqrt{25-c^2}$

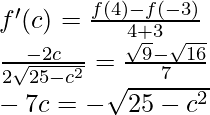
On squaring both sides, we get

49c² = 25 – c²

c² = 1/2 

c = ±1/√2 

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (x)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日平均值定理 f(x) = tan ^-1 x on [0, 1] 所示，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = tan^-1x

Here, the given f(x) is is continuous on [0, 1] and differentiable on (0, 1)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, 1) such that, 

$f'(c)=\frac{f(1)-f(0)}{1-0}\\ \frac{1}{1+c^2}=\frac{\tan^{-1}-\tan^{-1}(0)}{1}\\ \frac{1}{1+c^2}=\frac{\frac{π}{4}-0}{1}\\ \frac{4}{π}=1+c^2\\ c=\sqrt{\frac{4}{π}-1}$

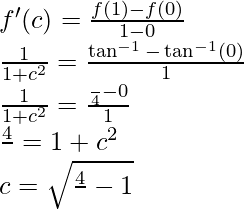
Hence, the Lagrange’s mean value theorem is verified.

问题 1 (xi)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日平均值定理 f(x) = x + 1/x on [1, 3] 所述，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = x + 1/x ⇒ (x² + 1)/x

Here, the given f(x) is continuous on [1, 3] and differentiable on (1, 3)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 3) such that, 

$f'(c)=\frac{f(3)-f(1)}{3-1}\\ 1-\frac{1}{c^2}=\frac{(3+\frac{1}{3}-(1+1))}{2}\\ 1-\frac{1}{c^2}=\frac{\frac{10}{3}-2}{2}\\ 1-\frac{1}{c^2}=\frac{4}{3*2}\\ 1-\frac{2}{3}=\frac{1}{c^2}$

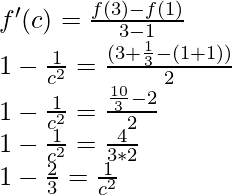
c² = 3

c = √3 ∈ (1, 3)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (xii)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日均值定理 f(x) = x (x + 4) ²在 [1, 3] 上所述，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = x (x + 4)²

Since the given f(x) = x (x + 4)² is a polynomial function. 

So, the given f(x) is continuous on [1, 3] and differentiable in (1, 3)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 3) such that, 

$f'(c)=\frac{f(4)-f(0)}{4-0}\\ 3c^2+16c+16=\frac{4*(8)^2-0}{4}$

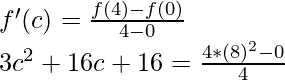
3c² + 16c + 16 = 64

3c² + 16c – 48 = 0

$c=\frac{-16±\sqrt{256+576}}{6}\\ =\frac{-16±8\sqrt{13}}{6}\\ c=\frac{-8±4\sqrt{13}}{3}\\ c=\frac{-8+4\sqrt{13}}{3}∈(0,4)$

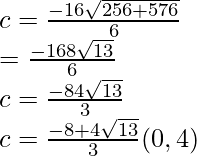
Hence, the Lagrange’s mean value theorem is verified.

问题 1 (xiii) 验证以下函数在指定区间上的拉格朗日均值定理。如拉格朗日均值定理 f(x) = x 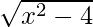$\sqrt{x^2-4}$在 [2, 4] 上。

解决方案：

Given that, 

f(x) = x$\sqrt{x^2-4}$

The given f(x) is exists, if 

x² – 4≥ 0

x² ≤ 4

x ≤ ±2

-2 < x < 2

So, f(x) has unique value ∀ x ∈(-2. 2), so the given f(x) is continuous on [2, 4].

Now, differentiate f(x) = (x² – 4)^1/2 with respect to x, we get

f'(x) = 1/2(x² – 4)^1/2-1d(x² – 4)/dx$=\frac{2x}{2\sqrt{x^2 - 4}} =\frac{x}{\sqrt{x^2 - 4}}$

So, f'(x) exists∀ x ∈ (2, 4), hence, f(x) is differential on (2, 4).

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (2, 4) such that, 

$f'(c)=\frac{f(4)-f(2)}{4-2}\\ \frac{c}{\sqrt{c^2-4}}=\frac{\sqrt{12}-0}{2}$

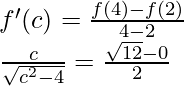
On squaring both sides, we get

⇒$\frac{c^2}{c^2-4}=\frac{12}{4}$

⇒4c² = 12c² – 48

⇒8c² = 48

⇒c² = 6

⇒c = √6 ∈ (2, 4)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (xiv)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日平均值定理 f(x) = x ² + x – 1 在 [0, 4] 上，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = x² + x – 1

Since the given f(x) = x² + x – 1 is a polynomial function. 

So, the given f(x) is continuous on [0, 4] and differentiable in (0, 4)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, 4) such that, 

$f'(c)=\frac{f(4)-f(0)}{4-0}\\ 2c+1=\frac{((4)^2+4-1)-(0-1)}{4}\\ 2c+1=\frac{19+1}{4}$

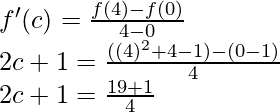
2c + 1 = 20/4

2c + 1 = 5

c = 2 ∈ (0, 4)

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (xv) 验证以下函数在指定区间上的拉格朗日均值定理。如拉格朗日平均值定理 f(x) = sin x – sin2x – x on [0, π] 所示，在每个指定区间中找到一个点“c”。

解决方案：

Given that, 

f(x) = sin x – sin2x – x

Since the given f(x) = sin x – sin2x – x is a polynomial function. 

So, the given f(x) is continuous on [0, π] and differentiable in (0, π)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, π) such that, 

$f'(c)=\frac{f(π)-f(0)}{π-0}\\ \cos c-2\cos2c-1=\frac{(\sinπ-sin2π-π)-(0)}{π}$ 

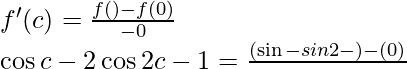
⇒cos c – 2cos2c = -1 + 1

⇒cos – 2(2cos²c – 1) = 0

⇒4cos2c – cosc – 2 = 0

⇒$\cos c-\frac{-1±\sqrt{1-4*4*(-2)}}{8}$

⇒$\cos c=\frac{1±\sqrt{33}}{8}$

⇒$c=\cos^{-1}(\frac{1±\sqrt{33}}{8})∈(0,π)$

Hence, the Lagrange’s mean value theorem is verified.

问题 1 (xvi)。在指定的间隔上验证以下函数的拉格朗日平均值定理。如拉格朗日平均值定理 f(x) = x ³ – 5x ² – 3x on [1, 3] 所示，在每个指定区间中找到一个点 'c'

解决方案：

Given that, 

 f(x) = x³ – 5x² – 3x

Since the given f(x) = x³ – 5x² – 3x is a polynomial function. 

So, the given f(x) is continuous on [1, 3] and differentiable in (1, 3)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 3) such that, 

$f'(c)=\frac{f(3)-f(1)}{3-1}$  

Now, f'(c) = 3c² – 10c – 3, f(1) = -7, f(3) = -27

3c² – 10c – 3 = $\frac{-27+ 7}{2}$

3c² – 10c – 3 = -10

3c² – 10c + 7 = 0

3c² – 3c – 7c + 7 = 0

c = 7/3, where c = 7/3 ∈ (1, 3) 

Hence, the Lagrange’s mean value theorem is verified.

问题 2. 讨论拉格朗日中值定理对函数f(x) = |x| 的适用性。在 [-1, 1] 上。

解决方案：

Given that, 

f(x) = |x| 

$f(x)= \begin{cases} -x,x<0\\ x,x\ge 0 \end{cases}$

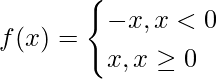
Now, we check differentiability at x = 0

LHD = 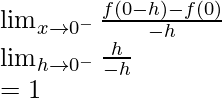$\lim_{x\to{0^-}}\frac{f(0-h)-f(0)}{-h}\\ \lim_{h\to{0^-}}\frac{h}{-h} \\=1\\$

RHD = 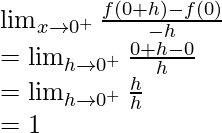$\lim_{x\to{0^+}}\frac{f(0+h)-f(0)}{-h}\\ =\lim_{h\to{0^+}}\frac{0+h-0}{h}\\ =\lim_{h\to{0^+}}\frac{h}{h}\\ =1$

LHD ≠ RHD

Here, f(x) is not differentiable at x = 0 ∈ (-1, 1)

Hence, the Lagrange’s mean value theorem is not applicable for the given f(x) = \x\.

问题 3. 证明拉格朗日均值定理不适用于 [-1, 1] 上的函数f(x) = 1/x。

解决方案：

Given that, 

f(x) = 1/x

On differentiating with respect to x, we get

$f'(x)=-\frac{1}{x^2}$

So, we conclude that f'(x) does not exist at x = 0 ∈ (-1, 1)

So, f(x) is also not differentiable in (-1, 1)

Hence, the Lagrange’s mean value theorem is not applicable for the given f(x) = 1/x.

问题 4. 验证函数f(x) 的拉格朗日均值定理的假设和结论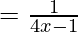$=\frac{1}{4x-1}$ , 1 ≤ x ≤ 4。

解决方案：

Given that, 

 f(x) $=\frac{1}{4x-1}$

Here, the given f(x) has a unique value for each x ∈ [1, 4], so f(x) is continuous in [1, 4].

Now differentiate f(x) with respect to x, we get

$f'(x)-\frac{4}{(4x-1)^2}$ 

So, here f'(x) exits for all x ∈ (1, 4), hence, f(x) is differentiable on (1, 4)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 4) such that,

$f'(c)=\frac{f(4)-f(1)}{4-1}\\ -\frac{4}{(4c-1)^2}=\frac{\frac{1}{15}-\frac{1}{3}}{3}\\ -\frac{4}{(4c-1)^2}=-\frac{4}{45}$

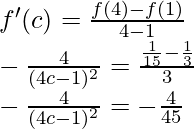
(4c – 1)² = 45

4c – 1 = ±3√5

$c=\frac{3\sqrt{5}+1}{4}∈[1,4]$

Hence, the Lagrange’s mean value theorem is verified.

问题 5. 在抛物线上求一点 y = (x – 4) ² ，其中切线平行于连接 (4, 0) 和 (5, 1) 的弦。

解决方案：

Given that, 

f(x) = y = (x – 4)²⇒ x² – 8x + 16  

Also it is given that the tangent is parallel to the chord joining (4, 0) and (5, 1)

So, let us considered the chord joining the points are (4, 5)

Since the given f(x) = x² – 8x + 16 is a polynomial function. 

So, the given f(x) is continuous on [4, 5] and differentiable in (4, 5)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (4, 5) such that, 

$f'(c)=\frac{f(b)-f(a)}{b-a}\\ 2(c-4)=\frac{f(5)-f(4)}{5-4}\\ 2c-8=\frac{1-0}{1}$

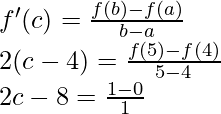
2c – 8 = 1

2c = 9

c = 9/2

So, 

f(c) = (c – 4)²

f(c) = (9/2 – 4)²

f(c) = 1/4

Hence, (c, f(c)) = (9/2, 1/4) is the given point.

问题 6. 在曲线 y = x ² + x 上找到一点，其中切线平行于连接 (0, 0) 和 (1, 2) 的弦。

解决方案：

Given that, 

f(x) = y = x² + x

Also it is given that the tangent is parallel to the chord joining (0, 0) and (1, 2)

So, let us considered the chord joining the points are (0, 1)

Since the given f(x) = x² + x is a polynomial function. 

So, the given f(x) is continuous on [0, 1] and differentiable in (0, 1)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (0, 1) such that, 

$f'(c)=\frac{f(b)-f(a)}{b-a}\\ 2c+1=\frac{f(1)-f(0)}{1-0}$

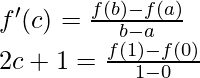
2c + 1 = 2

c = 1/2 

So, 

f(c) = c² + c

f(c) = (1/2)² + 1/2

f(c) = 3/4

Hence, (c, f(c)) = (1/2, 3/4) is the given point.

问题 7. 在可能的 y = (x – 3) ²上找到一个点，其中切线平行于连接 (3, 0) 和 (4, 1) 的弦。

解决方案：

Given that, 

f(x) = y = (x – 3)² = x² – 6x + 9

Also it is given that the tangent is parallel to the chord joining (3, 0) and (4, 1)

So, let us considered the chord joining the points are (3, 4)

Since the given f(x) = x² – 6x + 9 is a polynomial function. 

So, the given f(x) is continuous on [3, 4] and differentiable in (3, 4)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (3, 4) such that, 

$f'(c)=\frac{f(b)-f(a)}{b-a}\\ 2(c-3)=\frac{f(4)-f(3)}{4-3}\\ 2c-6=\frac{1-0}{1}$

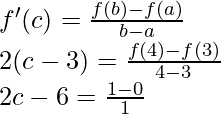
2c = 7

c = 7/2

So, 

f(c) = (c – 3)²

f(c) = (7/2 – 3)²

f(c) = 1/4

Hence, (c, f(c)) = (7/2, 1/4) is the given point.

问题 8. 找到曲线 y = x ³ – 3x 上的点，曲线的切线平行于连接 (1, -2) 和 (2, 2) 的弦。

解决方案：

Given that, 

f(x) = y = x³ – 3x

Also it is given that the tangent is parallel to the chord joining (1, -2) and (2, 2)

So, let us considered the chord joining the points are (1, 2)

Since the given f(x) = x³ – 3x is a polynomial function. 

So, the given f(x) is continuous on [1, 2] and differentiable in (1, 2)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 2) such that, 

$f'(c)=\frac{f(b)-f(a)}{b-a}\\ 3c^2-3=\frac{f(2)-f(1)}{2-1}\\ 3c^2-3=\frac{2+2}{1}\\ 3c^2=7\\ c=±\sqrt{\frac{7}{3}}$

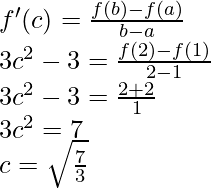
So, 

f(c) = ($\sqrt{\frac{7}{3}}$⁾³ – 3$\sqrt{\frac{7}{3}}$

f(c) = $±\frac{2}{3}\sqrt{\frac{7}{3}}$

Hence, (c, f(c)) = ($±\sqrt{\frac{7}{3}}, ±\frac{2}{3}\sqrt{\frac{7}{3}}$) is the given point.

问题 9. 在曲线 y = x ³ + 1 上找到切线平行于连接 (1, 2) 和 (3, 28) 的弦的点。

解决方案：

Given that, 

f(x) = y = x³ + 1

Also it is given that the tangent is parallel to the chord joining (1, 2) and (3, 28)

So, let us considered the chord joining the points are (1, 3)

Since the given f(x) = x³ + 1 is a polynomial function. 

So, the given f(x) is continuous on [1, 3] and differentiable in (1, 3)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (1, 3) such that, 

$f'(c)=\frac{f(b)-f(a)}{b-a}\\ 3c^2=\frac{f(3)-f(1)}{3-1}\\ 3c^2=\frac{28-2}{2}\\ c^2=\frac{13}{3}\\ c=\sqrt{\frac{13}{3}}$

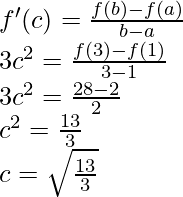
So, 

f(c) = c³ + 1

f(c) = ($\sqrt{\frac{13}{3}}$)³ + 1

Hence, (c, f(c)) = ($\sqrt{\frac{13}{3}}$, ($\sqrt{\frac{13}{3}}$)³ + 1) is the given point.

问题 10. 设 c 为参数定义为 x = a cos ³ θ , y = a sin ³ θ , 0 ≤ θ ≤ π/2 的曲线。确定 C 上的点 P，其中 C 的切线平行于连接点 (a, 0) 和 (0, a) 的弦。

解决方案：

Let us considered point P be (x, y)

So, given that,

x = a cos³θ  ….(1)

y = a sin³θ ….(2)

Now we find the slope of tangent 

$\frac{dy}{dx} = \frac{\frac{dy}{d\theta}}{\frac{dx}{d\theta}}$  ….(3)

So, differentiate eq(1), w.r.t. θ, we get,

dx/dθ = -3acos²θsinθ

Now, differentiate eq(2), w.r.t. θ, we get,

dx/dθ = 3a sin²θcosθ

Now put all these values in eq(3), we get

dy/dx =  -3acos²θsinθ/3a sin²θcosθ = -tanθ

Now the two given points are (a, 0) and (0, a).

So, the slope of the given chord , m = a – 0/0 – a = -1

According to the question it is given that point C is parallel to the chord

So, slope of tangent = slope of the chord

-tanθ = -1

θ = π/4

Now put the value of θ in eq(1) and (2), we get tha values of point P

x = a cos³(π/4) = a/2√2

y = a sin³(π/4) = a/2√2

So, the point P(a/2√2, a/2√2)

问题 11. 使用拉格朗日中值定理，证明 (b – a)sec ² a < tanb – tana < (b – a)sec ² b 其中 0 < a < b < π/2。

解决方案：

Given that, 

f(x) = tan x, x ∈ [a, b] such that 0 < a < b < π/2}

So, the given f(x) is continuous on [a, b] and differentiable in (a, b)

Hence, both the conditions of Lagrange’s mean value theorem are satisfied.

So, there exist a point c ∈ (a, b) such that, 

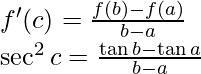$f'(c)=\frac{f(b)-f(a)}{b-a}\\ \sec^2c=\frac{\tan b-\tan a}{b-a}\space$….(i)

So, c ∈ (a, b)

sec²a < $(\frac{\tan b-\tan a}{b-a})<sec^2b$

Now, using eq(i), we get

(b – a)sec²a < (tan b – tan a) < (b – a)sec²b