9类RD Sharma解决方案–第15章平行四边形和三角形的区域-练习15.3 |套装1

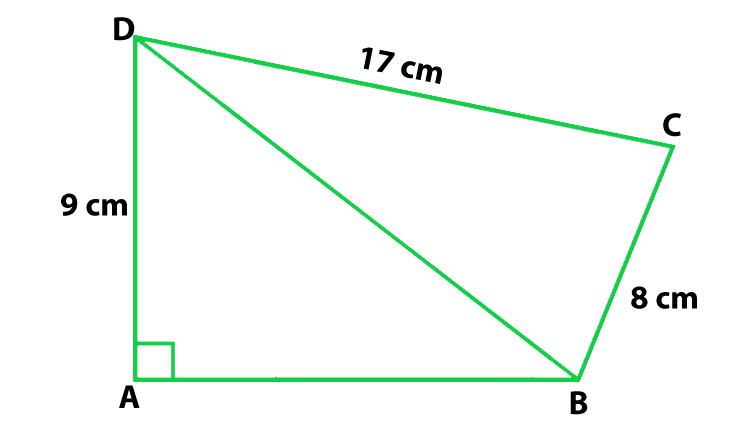
问题1.在图中，计算四边形ABCD的面积。

解决方案：

According to the question

DC = 17 cm, AD = 9 cm and BC = 8 cm

Find: the area of quadrilateral ABCD

In ΔBCD, 

Using Pythagoras Theorem

CD² = BD² + BC²                   

17² = BD² + 8²

BD² = 289 − 64

BD = 15

So, the area of ΔBCD = 1/2(8 × 17) = 68

In ΔABD 

Using Pythagoras Theorem

AB² + AD² = BD²                        

15² = AB² + 9²

AB² = 225 − 81 = 144

AB = 12

So, the area of ΔABD = 1/2(12 × 9) = 54

Now we find the ar(quad ABCD) = ar(ΔABD) + ar(ΔBCD)

ar(quad ABCD) = 54 + 68 = 122 cm²

Hence, the area of quadrilateral ABCD is 122 cm²

问题2。在图中，PQRS是一个正方形，T和U分别是PS和QR的中点。如果PQ = 8 cm，则找到ΔOTS的面积。

解决方案：

According to the question

T and U are mid-points of PS and QR 

Hence, TU ∥ PQ

PQ = 8 cm

Find: the area of ΔOTS

In ΔPQS, 

It is given that T is the midpoint of PS and TO ∥ PQ

therefore, TO = (1/2) PQ = 4 cm

and TS = (1/2) PS = 4 cm

So, the area of ar(ΔOTS) = (1/2)(TO × TS) 

= (1/2)(4 × 4) = 8 cm²

Hence, the area of ΔOTS is 8 cm²

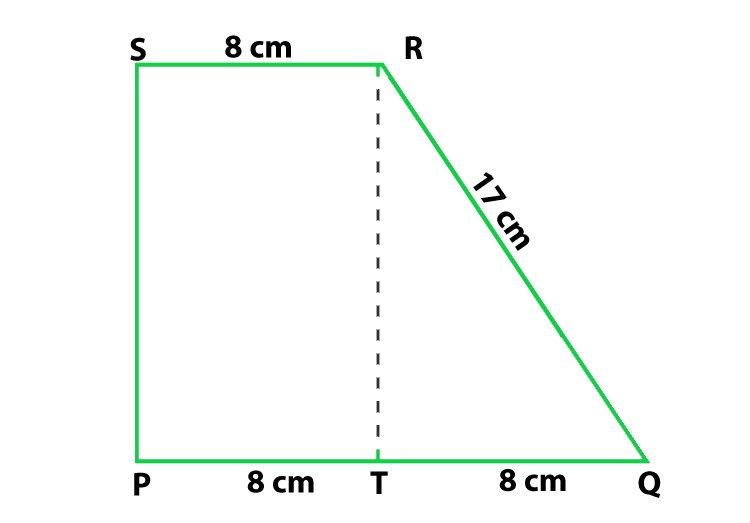
问题3.计算图中梯形PQRS的面积

解决方案：

According to the figure

PQ = 16 cm

Here T is the mid-point of side PQ so

PT = QT = 8 cm

SR = 8 cm

RQ = 17 cm

Find: the area of trapezium PQRS

So, the ar(trap. PQRS) = ar(rect. PSRT) + ar(ΔQRT)  ….(1)

So, In ΔQRT

Using Pythagoras Theorem

QR² = QT² + RT²                  

RT² = QR² − QT²

RT² = 17² − 8² = 225

RT = 15

So, the area of ΔQRT 

= 1/2(QT × RT) = 8 × 15 = 180/2 = 60

Now we find the area of rectangle PSRT

= PT × RT = 8 × 15 = 120

Now put all these values in eq(1), we get

ar(trap. PQRS) = 120 + 60 = 180

Hence, the area of trapezium is 180 cm²

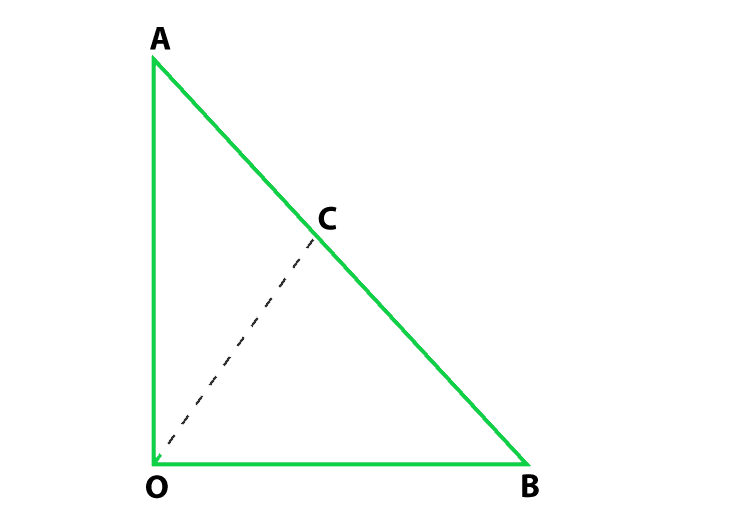
问题4.在图中，, AOB = 90°，AC = BC，OA = 12 cm，OC = 6.5 cm。找出ΔAOB的面积。

解决方案：

According to the question

∠AOB = 90°, AC = BC, OA = 12 cm and OC = 6.5 cm

Find: the area of ΔAOB

From the figure, C is the mid-point of hypotenuse AB so in right triangle

the mid-point is equidistant from the vertices

therefore, CA = CB = OC

CA = CB = 6.5 cm

AB = 13 cm

In ΔOAB, 

Using Pythagoras Theorem

AB² = OB² + OA²                               

13² = OB² + 12²

OB² = 13² − 12² = 169 − 144 = 25

OB = 5

Now we find the area of ΔAOB = (1/2)(12 × 5) = 30 cm²

Hence, the area of ΔAOB is 30 cm²

问题5.在图中，ABCD是一个梯形，其中AB = 7 cm，AD = BC = 5 cm，DC = x cm，AB与DC之间的距离为4 cm。求出x的值和梯形ABCD的面积。

解决方案：

According to the question

AB = 7 cm, AD = BC = 5 cm

Construction: Draw AL ⊥ DC, BM ⊥ DC,

AL = BM = 4 cm and LM = 7 cm

Find: the value of x and area of trapezium ABCD.

In Δ ADL,

Using Pythagoras Theorem

AD² = AL² + DL²          

25 = 16 + DL²

DL = 3 cm

Similarly,

MC = √BC² – BM² = √25 – 16 = 3 cm                              

So, x = CD = CM + ML + LD = (3 + 7 + 3) cm = 13 cm

Now we find the area of trapezium ABCD = 1/2(AB + CD) × AL 

= 1/2(7 + 13) × 4 cm² = 40 cm²

Hence, the value of x is 3 cm and the area of trapezium is 40 cm²

问题6.在图中，OCDE是一个矩形，刻在半径为10 cm的圆的象限中。如果OE =2√5cm，则找到矩形的面积。

解决方案：

According to the question

OD = 10 cm and OE = 2√5cm

Find: the area of the rectangle OCDE

So, In ΔDEO

By using Pythagoras theorem

OD² = OE² + DE²

DE = √OD² – OE² 

= √10² – (2√5)² = 4√5 cm

Now we find the area of rectangle OCDE = OE × DE

= 2√5 x 4√5 cm² = 40 cm²

Hence, the area of rectangle is 40 cm²

问题7。在图中，ABCD是一个梯形，其中AB∥DC。证明ar(ΔAOD)= ar(ΔBOC)

解决方案：

According to the question

ABCD is a trapezium in which AB ∥ DC

To prove : ar(ΔAOD) = ar(ΔBOC)

Proof : 

According to the figure, we conclude that ΔADC and ΔBDC are on the 

same base DC and between same parallels AB and DC

So, ar(ΔADC) = ar(ΔBDC) ….(1)

Here, ar(ΔADC) = ar(ΔAOD) + ar(ΔDOC) 

Similarly, ar(ΔBDC) = ar(ΔBOC) + ar(ΔDOC)

Now put all these values in eq(1), we get

ar(ΔAOD) + ar(ΔDOC) = ar(ΔBOC) + ar(ΔDOC)

ar(ΔAOD) = ar(ΔBOC)

Hence, proved

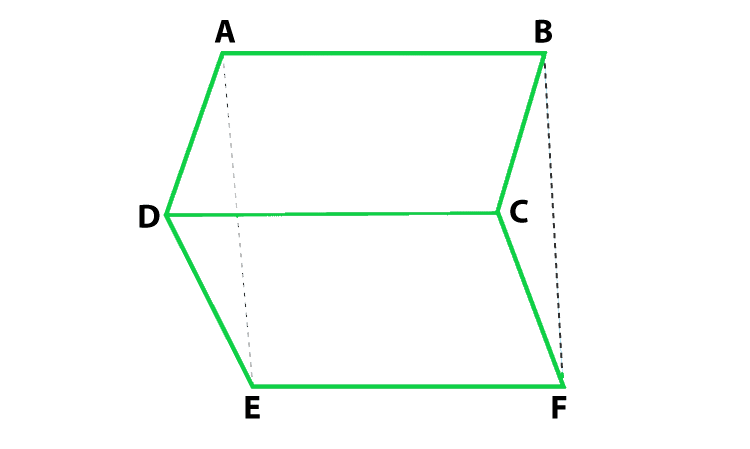
问题8.在图中，ABCD，ABFE和CDEF是平行四边形。证明ar(ΔADE)= ar(ΔBCF)。

解决方案：

According to the question

ABCD is parallelogram, so, AD = BC

CDEF is parallelogram, so, DE = CF

ABFE is parallelogram, so, AE = BF

Prove: ar(ΔADE) = ar(ΔBCF)

Proof:

In ΔADF and BCF,

AD = BC, 

DE = CF 

AE = BF

So, by SSS congruence, 

ΔADE ≅ ΔBCF

So, ar(ΔADE) = ar(ΔBCF)

Hence, proved

问题9.四边形ABCD的对角AC和BD在P处相交。表明：ar(ΔAPB)×ar(ΔCPD)= ar(ΔAPD)×ar(ΔBPC)。

解决方案：

Construction : Draw BQ ⊥ AC and DR ⊥ AC

Prove: ar(ΔAPB) × ar(ΔCPD) = ar(ΔAPD) × ar(ΔBPC)

Proof: 

Lets take L.H.S

= ar(ΔAPB) × ar(ΔCDP)

= (1/2) [(AP × BQ)] × (1/2 × PC × DR)

= (1/2 × PC × BQ) × (1/2 × AP × DR)

= ar(ΔAPD) × ar(ΔBPC)

L.H.S = R.H.S

Hence proved

问题10.在图中，ABC和ABD是基础AB上的两个三角形。如果线段CD被AB在O处平分，则表明ar(ΔABC)= ar(ΔABD)。

解决方案：

According to the question

ABC and ABD are two triangles on the base AB

and CD is bisected by AB at O,

To prove: ar(ΔABC) = ar(ΔABD).

Construction: CP ⊥ AB and DQ ⊥ AB.

Proof: 

First we find the area of ΔABC = 1/2 × AB × CP         …..(i)

Now we find the area of ΔABD = 1/2 × AB × DQ              …..(i)

So, in ΔCPO and ΔDQO,

∠CPO = ∠DQO           (Each 90°)

CO = OD                    (Given)

∠COP = ∠DOQ                           (Vertically opposite angles are equal)

So, by AAS congruency

ΔCPO ≅ ΔDQO            

So, by C.P.C.T

CP = DQ        …..(iii)                           

So, from equation (i), (ii), and (iii)

ar(ΔABC) = ar(ΔABD)

Hence proved